log1p和expm1

在数据预处理时首先可以对偏度比较大的数据用log1p函数进行转化，使其更加服从高斯分布，此步处理可能会使我们后续的分类结果得到一个更好的结果；
平滑处理很容易被忽略掉，导致模型的结果总是达不到一定的标准，同样使用逼格更高的log1p能避免复值得问题——复值指一个自变量对应多个因变量；

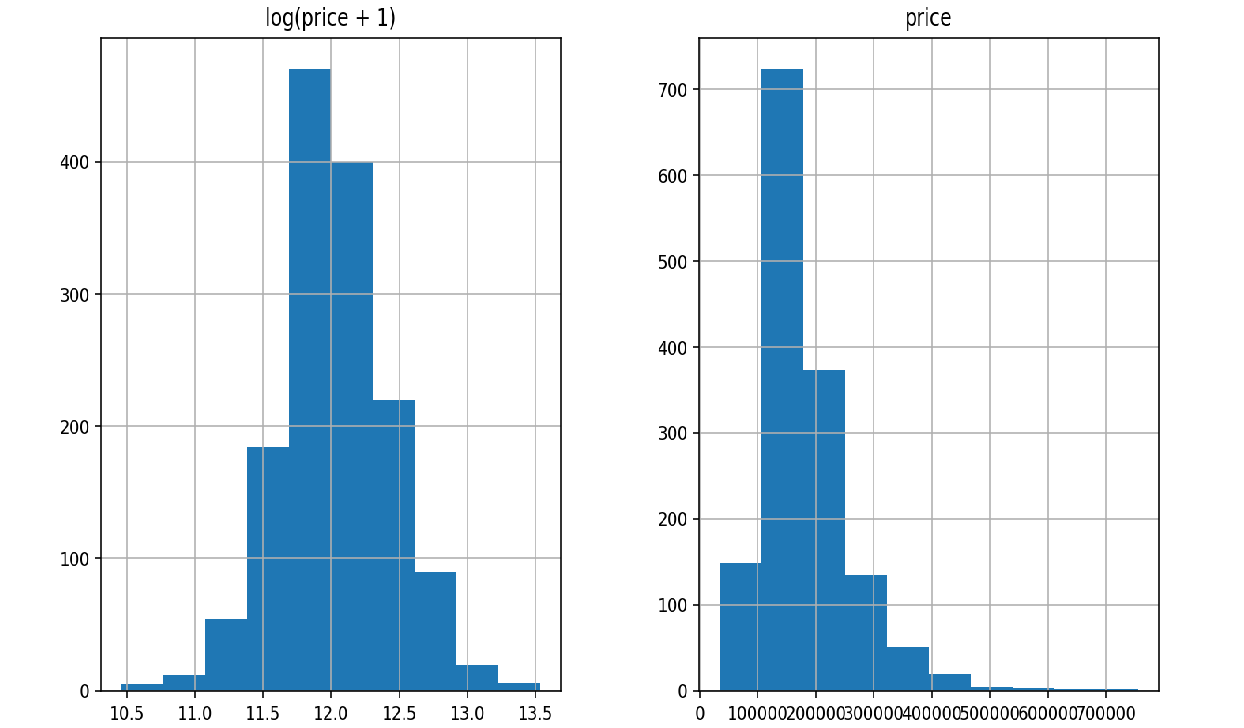
log1p的使用就像是将一个数据压缩到了一个区间，与数据的标准化类似。它的逆运算是expm1函数。

log1p :=       即

expm1 := 

log1p函数有它存在的意义，即保证了x数据的有效性，当x很小时（如 两个数值相减后得到），由于太小超过数值有效性，用计算得到结果为0，

换作log1p则计算得到一个很小却不为0的结果，这便是它的意义（好像是用泰勒公式来展开运算的，不确定）。

同样的道理对于expm1，当x特别小，就会急剧下降出现如上问题，甚至出现错误值。

另外RMSLE（均方根对数误差）会更多的惩罚欠拟合，所以在使用该误差定义时我们也可以用到上面的函数：

1. np.loglp计算加一后的对数，其逆运算是np.expm1；
2. 采用此误差函数时，可以先对原始数据做np.log1p，再使用RMSE。