堆排序（大顶堆、小顶堆）----C语言

堆排序

之前的随笔写了栈（顺序栈、链式栈）、队列（循环队列、链式队列）、链表、二叉树，这次随笔来写堆

1、什么是堆？

堆是一种非线性结构，（本篇随笔主要分析堆的数组实现）可以把堆看作一个数组，也可以被看作一个完全二叉树，通俗来讲堆其实就是利用完全二叉树的结构来维护的一维数组

按照堆的特点可以把堆分为大顶堆和小顶堆

大顶堆：每个结点的值都大于或等于其左右孩子结点的值

小顶堆：每个结点的值都小于或等于其左右孩子结点的值

（堆的这种特性非常的有用，堆常常被当做优先队列使用，因为可以快速的访问到“最重要”的元素）

2、堆的特点（数组实现）

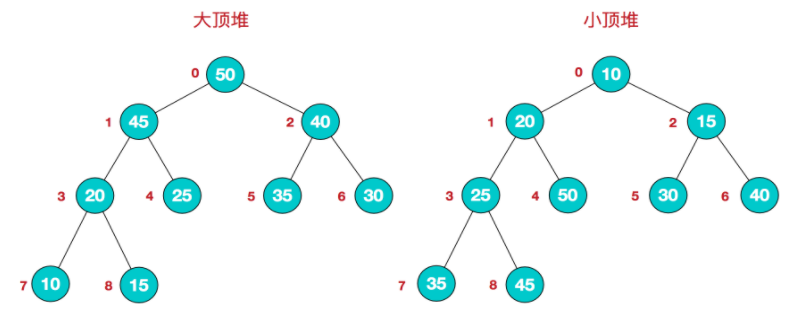
（图片来源：https://www.cnblogs.com/chengxiao/p/6129630.html）

我们对堆中的结点按层进行编号，将这种逻辑结构映射到数组中就是下面这个样子

（图片来源：https://www.cnblogs.com/chengxiao/p/6129630.html）

我们用简单的公式来描述一下堆的定义就是：（读者可以对照上图的数组来理解下面两个公式）

大顶堆：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]

小顶堆：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]

3、堆和普通树的区别

内存占用：

普通树占用的内存空间比它们存储的数据要多。你必须为节点对象以及左/右子节点指针分配额外的内存。堆仅仅使用数组，且不使用指针

（可以使用普通树来模拟堆，但空间浪费比较大，不太建议这么做）

平衡：

二叉搜索树必须是“平衡”的情况下，其大部分操作的复杂度才能达到O(nlog₂n)。你可以按任意顺序位置插入/删除数据，或者使用 AVL 树或者红黑树，但是在堆中实际上不需要整棵树都是有序的。我们只需要满足对属性即可，所以在堆中平衡不是问题。因为堆中数据的组织方式可以保证O(nlog₂n) 的性能

搜索：

在二叉树中搜索会很快，但是在堆中搜索会很慢。在堆中搜索不是第一优先级，因为使用堆的目的是将最大（或者最小）的节点放在最前面，从而快速的进行相关插入、删除操作

 

4、堆排序的过程

先了解下堆排序的基本思想：

将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值，

如此反复执行，便能得到一个有序序列了，建立最大堆时是从最后一个非叶子节点开始从下往上调整的（这句话可能不好太理解），下面会举一个例子来理解堆排序的基本思想

给一个无序序列如下

int a[] = {, , , , , };

现在可以根据数组将完全二叉树还原出来

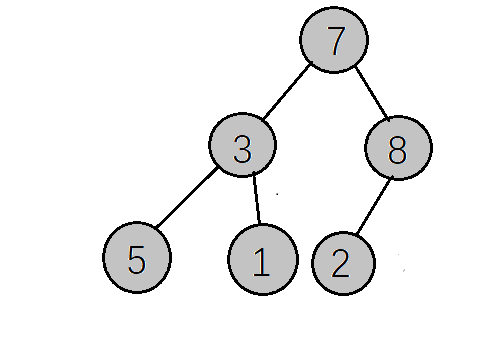
好了，现在我们要做的事情就是要把7，3，8，5，1，2变成一个有序的序列，如果想要升序就是1，2，3，5，7，8   如果想要降序就是8，7，5，3，2，1 ，这两种就是我们要的最终结果，然后我们就可以根据我们想要的结果来选择

适合类型的堆来进行排序

升序----使用大顶堆

降序----使用小顶堆

5、为什么升序要用大顶堆呢

上面提到过大顶堆的特点：每个结点的值都大于或等于其左右孩子结点的值，我们把大顶堆构建完毕后根节点的值一定是最大的，然后把根节点的和最后一个元素（也可以说最后一个节点）交换位置，那么末尾元素此时就是最大元素了（理解这点很重要）

知道了堆排序的原理下面就可以来操作了，在进行操作前先理清一下步骤

（假设我们想要升序的排列）

第一步：先n个元素的无序序列，构建成大顶堆

第二步：将根节点与最后一个元素交换位置，（将最大元素"沉"到数组末端）

第三步：交换过后可能不再满足大顶堆的条件，所以需要将剩下的n-1个元素重新构建成大顶堆

第四步：重复第二步、第三步直到整个数组排序完成

6、图解交换过程（得到升序序列，使用大顶堆来调整）

这里以int a[6] = {7, 3, 8, 5, 1, 2}为例子

先要找到最后一个非叶子节点，数组的长度为6，那么最后一个非叶子节点就是：长度/2-1，也就是6/2-1=2，然后下一步就是比较该节点值和它的子树值，如果该节点小于其左\右子树的值就交换（意思就是将最大的值放到该节点）

8只有一个左子树，左子树的值为2，8>2不需要调整

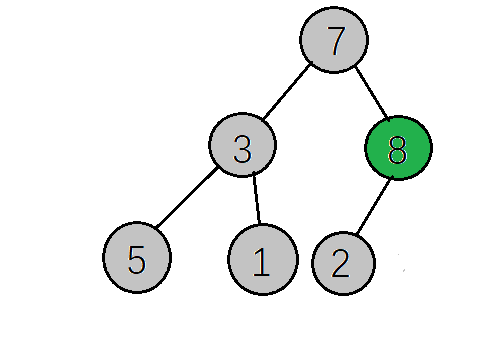
下一步，继续找到下一个非叶子节点（其实就是当前坐标-1就行了），该节点的值为3小于其左子树的值，交换值，交换后该节点值为5，大于其右子树的值，不需要交换

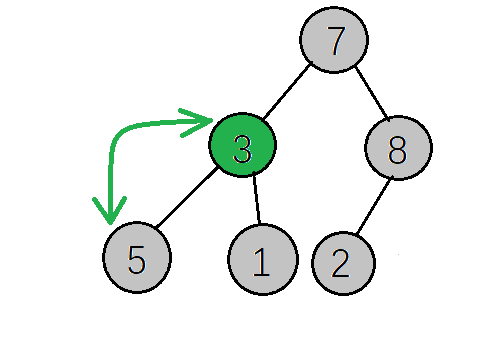
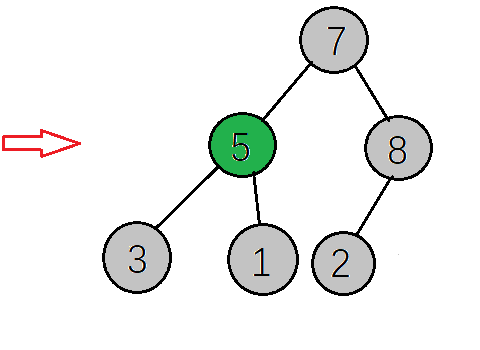
下一步，继续找到下一个非叶子节点，该节点的值为7，大于其左子树的值，不需要交换，再看右子树，该节点的值小于右子树的值，需要交换值

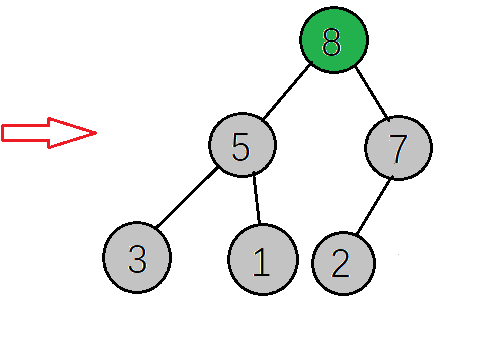
下一步，检查调整后的子树，是否满足大顶堆性质，如果不满足则继续调整（这里因为只将右子树的值与根节点互换，只需要检查右子树是否满足，而7>2刚好满足大顶堆的性质，就不需要调整了，

如果运气不好整个树的根节点的值是1，那么就还需要调整右子树）

到这里大顶堆的构建就算完成了，然后下一步交换根节点（8）与最后一个元素（2）交换位置（将最大元素"沉"到数组末端），此时最大的元素就归位了，然后对剩下的5个元素重复上面的操作

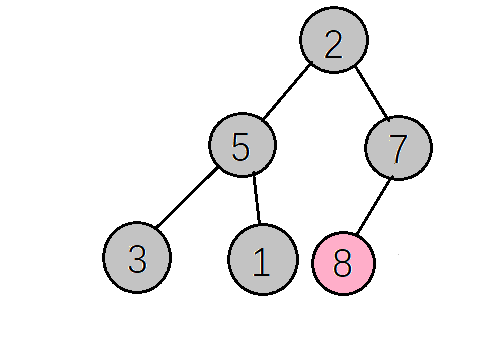（这里用粉红色来表示已经归位的元素）

剩下只有5个元素，最后一个非叶子节点是5/2-1=1，该节点的值（5）大于左子树的值（3）也大于右子树的值（1），满足大顶堆性质不需要交换

找到下一个非叶子节点，该节点的值（2）小于左子树的值（5），交换值，交换后左子树不再满足大顶堆的性质再调整左子树，左子树满足要求后再返回去看根节点，根节点的值（5）小于右子树的值（7），再次交换值

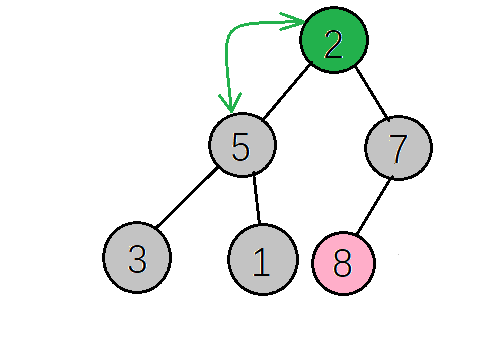
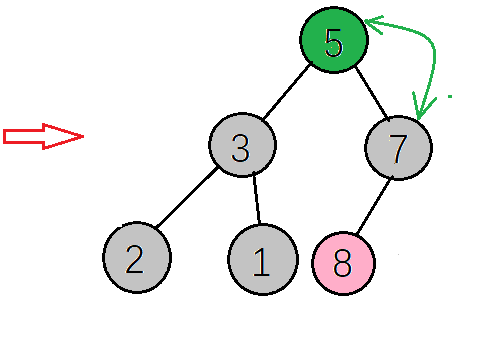
得到新的大顶堆，如下图，再把根节点的值（7）与当前数组最后一个元素值（1）交换，再重构大顶堆->交换值->重构大顶堆->交换值····，直到整个数组都变成有序序列

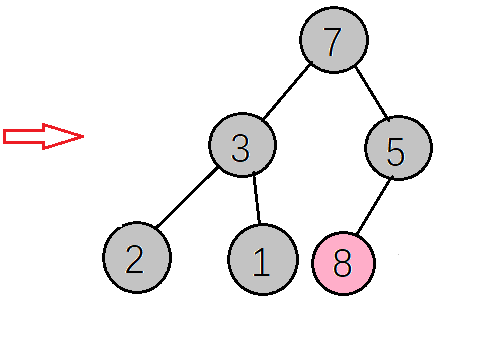
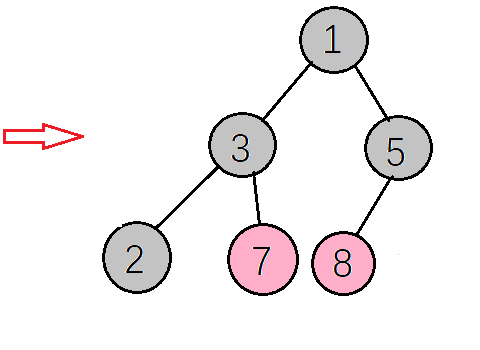
最后得到的升序序列如下图

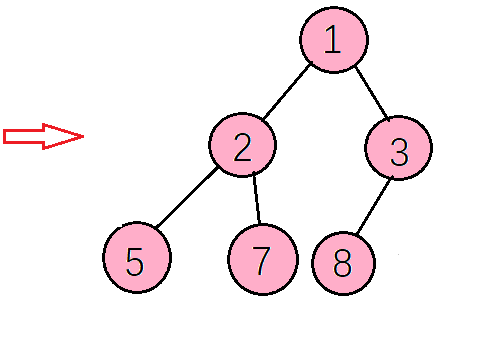
7、堆排序的代码实现

上面说了一大堆来详细说明堆排序的操作步骤，下面开始就开始来码代码了

笔者将堆排序的过程分成了两个子函数

void Swap(int *heap, int len);        /* 交换根节点和数组末尾元素的值 */
void BuildMaxHeap(int *heap, int len);/* 构建大顶堆 */

先来实现构建大堆的部分：

 /* Function: 构建大顶堆 */
 void BuildMaxHeap(int *heap, int len)
 {
     int i;
     int temp;

     for (i = len/-; i >= ; i--)
     {
         if ((*i+) < len && heap[i] < heap[*i+])    /* 根节点小于左子树 */
         {
             temp = heap[i];
             heap[i] = heap[*i+];
             heap[*i+] = temp;
             /* 检查交换后的左子树是否满足大顶堆性质 如果不满足 则重新调整子树结构 */
             if ((*(*i+)+ < len && heap[*i+] < heap[*(*i+)+]) || (*(*i+)+ < len && heap[*i+] < heap[*(*i+)+]))
             {
                 BuildMaxHeap(heap, len);
             }
         }
         if ((*i+) < len && heap[i] < heap[*i+])    /* 根节点小于右子树 */
         {
             temp = heap[i];
             heap[i] = heap[*i+];
             heap[*i+] = temp;
             /* 检查交换后的右子树是否满足大顶堆性质 如果不满足 则重新调整子树结构 */
             if ((*(*i+)+ < len && heap[*i+] < heap[*(*i+)+]) || (*(*i+)+ < len && heap[*i+] < heap[*(*i+)+]))
             {
                 BuildMaxHeap(heap, len);
             }
         }
     }
 }

上述代码中不易于理解的可能就是下面这条if判断语句

 /* 检查交换后的左子树是否满足大顶堆性质 如果不满足 则重新调整子树结构 */
 if ((*(*i+)+ < len && heap[*i+] < heap[*(*i+)+]) || (*(*i+)+ < len && heap[*i+] < heap[*(*i+)+]))
 {
       BuildMaxHeap(heap, len);
 }

把if里面的条件分来开看2*(2*i+1)+1 < len的作用是判断该左子树有没有左子树（可能有点绕），heap[2*i+1] < heap[2*(2*i+1)+1]就是判断左子树的左子树的值是否大于左子树，如果是，那么就意味着交换值

过后左子树大顶堆的性质被破环了，需要重构该左子树

下面来实现交换部分

 /* Function: 交换交换根节点和数组末尾元素的值*/
 void Swap(int *heap, int len)
 {
     int temp;

     temp = heap[];
     heap[] = heap[len-];
     heap[len-] = temp;
 }

然后来考虑下主函数部分，因为是int a[6] = {7, 3, 8, 5, 1, 2}长度为6，需要构建大顶堆，交换值6次才能得到有序序列，由此可以确定主函数的for循环为,for (i = len; i > 0; i--)

 int main()
 {
     int a[] = {, , , , , };
     int len = ;    /* 数组长度 */
     int i;

     for (i = len; i > ; i--)
     {
         BuildMaxHeap(a, i);
         Swap(a, i);
     }
     for (i = ; i < len; i++)
     {
         printf("%d ", a[i]);
     }

     return ;
 }

下面附上堆排序完整代码：

 #include <stdio.h>

 void Swap(int *heap, int len);        /* 交换根节点和数组末尾元素的值 */
 void BuildMaxHeap(int *heap, int len);/* 构建大顶堆 */

 int main()
 {
     int a[] = {, , , , , };
     int len = ;    /* 数组长度 */
     int i;

     for (i = len; i > ; i--)
     {
         BuildMaxHeap(a, i);
         Swap(a, i);
     }
     for (i = ; i < len; i++)
     {
         printf("%d ", a[i]);
     }

     return ;
 }
 /* Function: 构建大顶堆 */
 void BuildMaxHeap(int *heap, int len)
 {
     int i;
     int temp;

     for (i = len/-; i >= ; i--)
     {
         if ((*i+) < len && heap[i] < heap[*i+])    /* 根节点大于左子树 */
         {
             temp = heap[i];
             heap[i] = heap[*i+];
             heap[*i+] = temp;
             /* 检查交换后的左子树是否满足大顶堆性质 如果不满足 则重新调整子树结构 */
             if ((*(*i+)+ < len && heap[*i+] < heap[*(*i+)+]) || (*(*i+)+ < len && heap[*i+] < heap[*(*i+)+]))
             {
                 BuildMaxHeap(heap, len);
             }
         }
         if ((*i+) < len && heap[i] < heap[*i+])    /* 根节点大于右子树 */
         {
             temp = heap[i];
             heap[i] = heap[*i+];
             heap[*i+] = temp;
             /* 检查交换后的右子树是否满足大顶堆性质 如果不满足 则重新调整子树结构 */
             if ((*(*i+)+ < len && heap[*i+] < heap[*(*i+)+]) || (*(*i+)+ < len && heap[*i+] < heap[*(*i+)+]))
             {
                 BuildMaxHeap(heap, len);
             }
         }
     }
 }

 /* Function: 交换交换根节点和数组末尾元素的值*/
 void Swap(int *heap, int len)
 {
     int temp;

     temp = heap[];
     heap[] = heap[len-];
     heap[len-] = temp;
 }

运行结果：

虽然STL模板库给我们提供了两种简单方便堆操作的方式，很多高级语言的也有很多常见数据结构的封装，笔者还是建议需要学习数据结构相关的内容，至少要了解不同的数据结构

避免在使用高级语言的封装好的数据结构时出现只会用不理解的尴尬情况····