BZOJ4816 Sdoi2017数字表格

一开始只推出O(TN)的做法，后来看了看发现再推一步就好了。

我们只需要枚举gcd就可以啦。

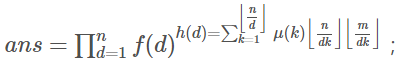
然后我们改变一下枚举顺序

设T为dk

预处理中间那部分前缀积就好了。

 #include<bits/stdc++.h>
 using namespace std;
 const int N=1e6+,mod=1e9+;
 int n,m,p[N/],miu[N],g[N],f[N],inv[N],cnt;bool v[N];
 typedef long long ll;
 int qmod(int x,ll y)
 {
     int ans=;
     while(y)
     {
         if(y&)ans=1ll*ans*x%mod;
         x=1ll*x*x%mod;y>>=;
     }
     return ans;
 }
 void init()
 {
     miu[]=;
     for(int i=;i<=1e6;++i)
     {
         if(!v[i])
         {
             p[++cnt]=i;miu[i]=-;
         }
         for(int j=;j<=cnt&&i*p[j]<=1e6;++j)
         {
             v[i*p[j]]=;
             if(i%p[j]==)break;
             miu[i*p[j]]=-miu[i];
         }
     }
     for(int i=;i<=1e6;++i)g[i]=;
     f[]=;f[]=g[]=;
     for(int i=;i<=1e6;++i)f[i]=(f[i-]+f[i-])%mod;
     for(int i=;i<=1e6;++i)
     {
         inv[i]=qmod(f[i],mod-);
         for(int j=i,k=;j<=1e6;j+=i,k++)
         if(miu[k])
         {
             if(miu[k]==-)
             g[j]=1ll*g[j]*inv[i]%mod;
             else
             g[j]=1ll*g[j]*f[i]%mod;
         }
         g[i]=1ll*g[i]*g[i-]%mod;
     }
     return;
 }
 int main()
 {
     init();int T;
     scanf("%d",&T);
     for(int k=;k<=T;++k)
     {
         scanf("%d%d",&n,&m);
         if(n>m)swap(n,m);int ans=;
         for(int i=,j;i<=n;i=j+)
         {
             j=min(n/(n/i),m/(m/i));
             ans=1ll*ans*qmod(1ll*g[j]*qmod(g[i-],mod-)%mod,1ll*(n/i)*(m/i))%mod;
         }
         printf("%d\n",(ans+mod)%mod);
     }
     return ;
 }