利用十字链表压缩稀疏矩阵（c++）-- 数据结构

题目：

7-1 稀疏矩阵 （30 分)

 

如果一个矩阵中，0元素占据了矩阵的大部分，那么这个矩阵称为“稀疏矩阵”。对于稀疏矩阵，传统的二维数组存储方式，会使用大量的内存来存储0，从而浪费大量内存。为此，可以用三元组的方式来存放一个稀疏矩阵。

对于一个给定的稀疏矩阵，设第r行、第c列值为v，且v不等于0，则这个值可以表示为 <r,v,c>。这个表示方法就称为三元组。那么，对于一个包含N个非零元素的稀疏矩阵，就可以用一个由N个三元组组成的表来存储了。

如：{<1, 1, 9>, <2, 3, 5>, <10, 20, 3>}就表示这样一个矩阵A：A[1,1]=9，A[2,3]=5，A[10,20]=3。其余元素为0。

要求查找某个非零数据是否在稀疏矩阵中，如果存在则输出其所在的行列号，不存在则输出ERROR。

输入格式:

共有N+2行输入： 第一行是三个整数m, n, N(N<=500)，分别表示稀疏矩阵的行数、列数和矩阵中非零元素的个数，数据之间用空格间隔; 随后N行，输入稀疏矩阵的非零元素所在的行、列号和非零元素的值； 最后一行输入要查询的非0数据k。

输出格式:

如果存在则输出其行列号，不存在则输出ERROR。

输入样例:

在这里给出一组输入。例如：

10 29 3
2 18 -10
7 1 98
8 10 2
2

输出样例:

在这里给出相应的输出。例如：

8 10

---

分析：

在矩阵中，若数值为0的元素数目远远多于非0元素的数目，并且非0元素分布没有规律时，则称该矩阵为稀疏矩阵。
为了更好地定义稀疏矩阵，引入稀疏因子 t =num/(n*m)[其中num为矩阵中非零元素个数，n为矩阵行数，m为矩阵列数]，
当t<=0.05时，该矩阵即可称作稀疏矩阵。 

压缩稀疏矩阵的常见方法有两种：
1.利用三元组表压缩
  优点：①代码简易；
       ②占用空间相对较小
  缺点：①无法实现随机存储；
       ②在进行对矩阵的操作（如矩阵的乘法/加法）矩阵中数据改变后，需要重新定义三元组表，不具有通用性，不灵活。

2.利用十字链表压缩
  优点：①能够实现随机存储；
       ②对于任意矩阵具有通用性
  缺点：①代码实现困难；
       ②占用空间相对较大

分析之后我们发现，相对于利用三元组表压缩稀疏矩阵，利用十字链表压缩应用的范围更为广阔，更具有实际操作意义。
这里我们采取十字链表方式进行压缩。

---

十字链表核心（难点）：

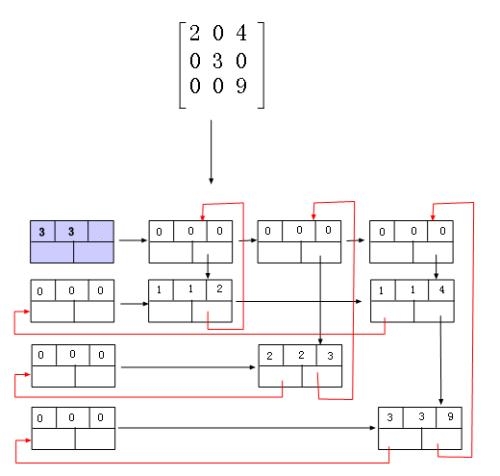
1.节点定义
（1）非零元素节点：
我们可以知道，十字链表说到底还是若干个循环链表，那么在创建十字链表之前我们需要构建一个合适的节点
所需信息：行（row)、列(col)、值(val)，该节点又要连接行的下一个节点（*right）以及列的下一个节点（*down）

如图：

（2）头节点定义
头节点与非零元素不同的是节点中row的位置存放的是原矩阵所有行数，col的位置存放的是原矩阵所有列数，且头节点需要指向一个指针数组（用于表示行列链表头）。
所需信息：行（row）、列（col)、指向指针数组*h[]的指针（*next)

如图：

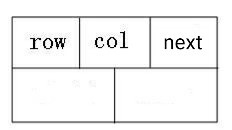
（3）行列链表头节点定义：
行列链表头的表示其实是利用指针数组实现的（存放指针的数组）*h[],这里为了方便，我们称为行列头指针。
所需信息：指向下一个行列链表头节点的指针（*next）、指向该行第一个非零元素的指针（*right)、指向该列第一个非零元素的指针（*down)

如图：

---

综上所述，为了实现定义节点操作时的一致性，我们会将节点定义如下图：

2.行列链表头节点在十字链表中的理解

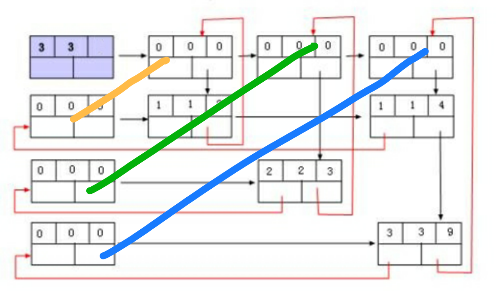
连线两端一个看上去像行头、另一个看上去像列头，其实这两个都是同一个*h[]。
我看到有建立两个指针数组的博客 https://blog.csdn.net/zhuyi2654715/article/details/6729783，即行链表头数组和列链表头数组，  
想必是误解了图的意思。

我是那么理解的：

3.当行/列中没有非零元素时的表示

前面提到，这是由若干个循环链表构成的十字链表，那么在空行/列的时候可以用行列头指针指向它自己本身来表示。
同理，当为行/列末时，最后一个节点的指针right/down必然是指向行/列头节点的。

---

代码：

#include<iostream>
using namespace std;

//定义十字链表节点
typedef struct matrinode{
    int i, j;
    struct matrinode *right, *down;
    union{
        int value;
        struct matrinode *next;
    }tag;
}matrinode;

//创建十字链表
//传入值：头节点指针，原矩阵行数，原矩阵列数
void createlist(matrinode *&head, int row, int column)
{
    int max = (row>column)?row:column;//取行列的最大值
    //定义指针数组（用于表示行列头），p、q、r辅助指针
    matrinode *h[max], *p, *q, *r;
    head = new matrinode;//申请头节点空间
    head->i = row;//将行数、列数存入头节点
    head->j = column;

    r = head;

    //行列链表头
    int count;
    for(count = ; count<max+; count++){//为了表示矩阵的行数和列数，这里从1开始计数
        h[count] = new matrinode;//给行列链表头申请空间
        h[count]->down = h[count]->right = h[count];
        h[count]->i = h[count]->j = ;
        r->tag.next = h[count];//head->h[1]->h[2]->...->h[max]
        r = h[count];
    }
    r->tag.next = head;//最后一个行列链表头节点指向head 

    int num;//非零元素个数
    int i, j, v;
    cin>>num;
    for(count=; count<num+; count++){
        p = new matrinode;
        cin>>i>>j>>v;
        p->i = i;
        p->j = j;
        p->tag.value = v;

        /*这里插入非零元素有两种情况：（以在某行插入为例）
        ①当行链表为空（q->right == h[count]）—或改元素列序数最大时 -> 插入到最后；
        ②非以上情况 -> 插入到某两节点中间
        */

        //行插入
        q = h[count];
        while(q->right != h[count] && q->right->j < j){
            q = q->right;
        }
        p->right = q->right;
        q->right = p;
        //列插入
        q = h[count];
        while(q->down != h[count] && q->down->i < i){
            q = q->down;
        }
        p->down = q->down;
        q->down = p;
    } 

}

//查找是否有符合条件的值
void search(matrinode *head)
{
    int value;//输入需要查找的值
    cin>>value;

    matrinode *h, *p;//定义两个辅助结点
    h = new matrinode;
    p = new matrinode;

    h = head->tag.next;//h指向h[1]
    p = h->right;//p指向h[1]第一行第一个元素
    int flag = ;//flag == 0表示找不到匹配值
    int i, j;//若找到满足条件的值时，i、j存放该值的行和列 

    while(h->tag.next != head){//当前行不是最后一行时
        if(p == h){//若该行为空
           h = h->tag.next;//移到下一行
           p = h->right;
        }else{//若该行非空
           if(p->tag.value != value){//若p节点存放的值！=需要查找的值时
               p = p->right;//p移动到该行下一个
           }else{//找到满足条件的值时
               i = p->i;
               j = p->j;
               flag = ;
               cout<<i<<" "<<j;
               break;
            }
        }
}
    if(flag == ){
        cout<<"ERROR";
    }    

 } 

int main(){
    matrinode *head;
    int row, column;
    cin>>row>>column;
    createlist(head, row, column);

    search(head);
    return ;
}

---

总结：

为了学会十字链表，查阅了很多资料，每份资料都不尽相同。这份代码是我打的第四份代码，因为参考的博客都不太一样，
比如有的博客会用到struct来定义一个十字链表，有的博客更喜欢用class囊括所有。从一开始的照猫画虎，到逐渐理解算法的核心思想，
需要经过不断的锻造，这也可能是我与代码互相折磨、互相成长的过程吧！

---

参考资料：

1.https://blog.csdn.net/xiangxizhishi/article/details/79119532

2.https://blog.csdn.net/TheLegendOfZelda/article/details/80221922

---