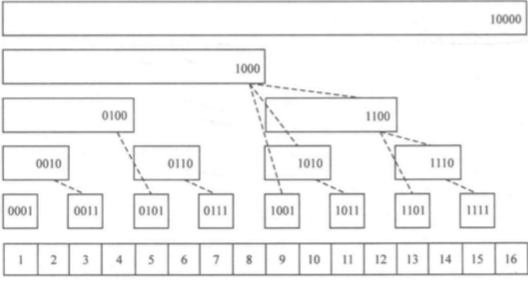
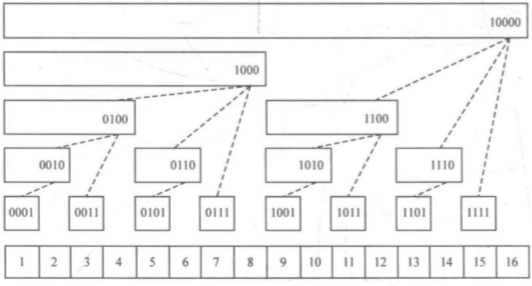
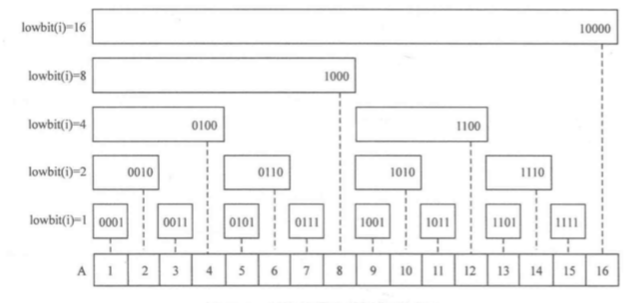
1057 Stack 树状数组

Stack is one of the most fundamental data structures, which is based on the principle of Last In First Out (LIFO). The basic operations include Push (inserting an element onto the top position) and Pop (deleting the top element). Now you are supposed to implement a stack with an extra operation: PeekMedian -- return the median value of all the elements in the stack. With N elements, the median value is defined to be the (N/2)-th smallest element if Nis even, or ((N+1)/2)-th if N is odd.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤10​5​​). Then Nlines follow, each contains a command in one of the following 3 formats:

where key is a positive integer no more than 10​5​​.

Output Specification:

For each Push command, insert key into the stack and output nothing. For each Pop or PeekMedian command, print in a line the corresponding returned value. If the command is invalid, print Invalid instead.

知识点：树状数组，二分查找

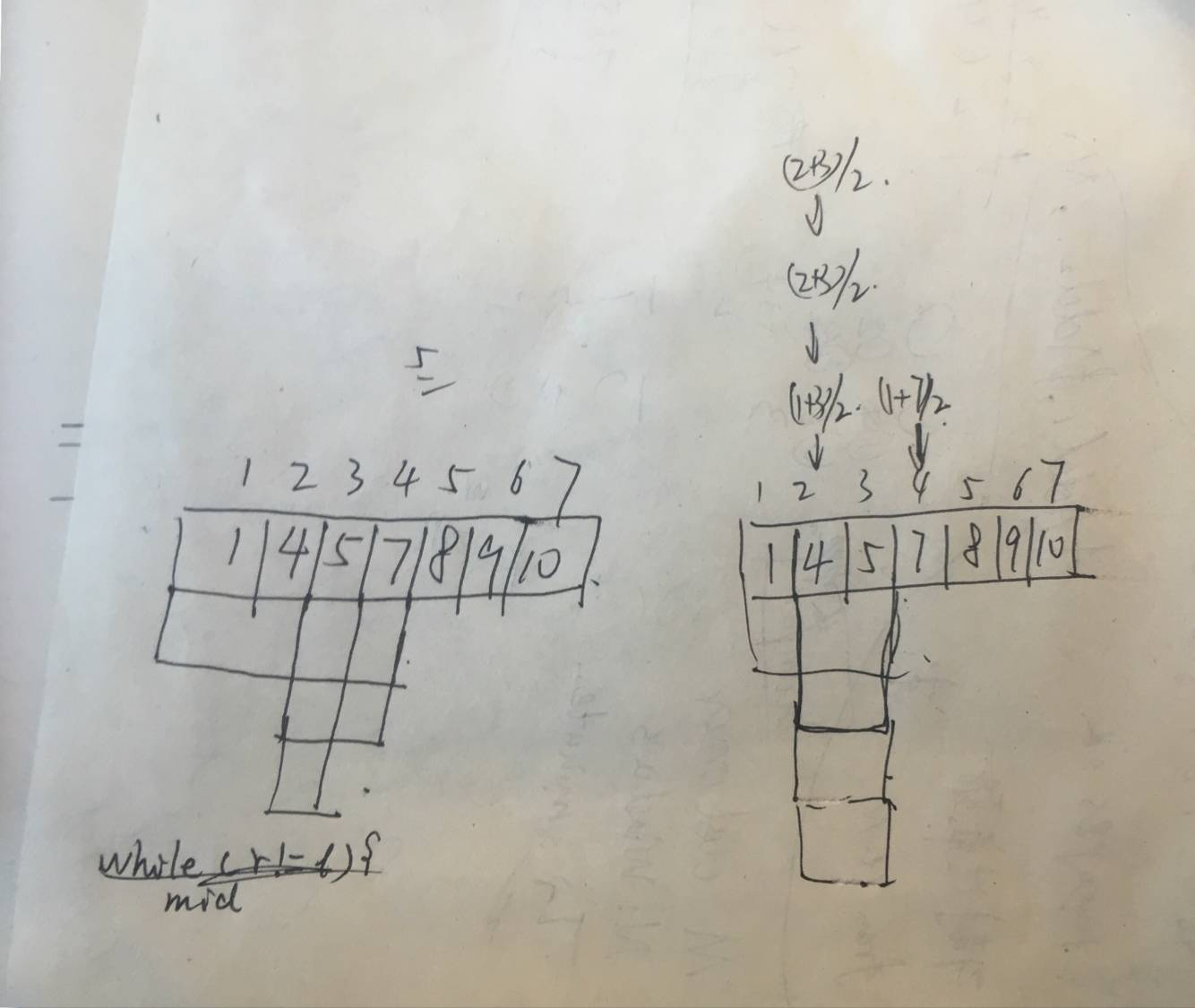
二分查找的写法

对比两种写法：

正确：

find(x){
	while(l!=r){
		mid=(l+r)/2;
		if(list[mid]>=x){
			r=mid;
		}else{
			l=mid+1;
		}
	}
}

错误：

find(x){
	while(l!=r){
		mid=(l+r)/2;
		if(list[mid]>x){
			r=mid-1;
		}else{
			l=mid;
		}
	}
}

 #include <iostream>
 #include <stack>
 using namespace std;
 const int maxn = ;

 int n;
 int c[maxn];
 stack<int> st;

 int lowbit(int v){  // lowbit()函数取二进制数最后一个1
     return v&(-v);
 }

15 int getSum(int x){  // 往前加和
16     int sum=0;
17     for(int i=x;i>0;i-=lowbit(i)){
18         sum += c[i];
19     }
20     return sum;
21 }

 void upDate(int v,int p){ // 往后更新
     for(int i=v;i<maxn;i+=lowbit(i)){
         c[i]+=p;
     }
 }

 int findMid(){
     printf("\n");
     int mid=(st.size()+)/;
     int l=, r=maxn-;
     int cnt=;
     while(l!=r&cnt<){ // 二分查找
         cnt++;
         printf("* %d %d\n",l,r);
         int m=(l+r)/;
         if(getSum(m)>=mid){
             r=m;
         }else{
             l=m+;
         }
     }
     return l;
 }

 int main(int argc, char *argv[]) {
     fill(c,c+maxn,);

     scanf("%d",&n);
     char cmd[]; int key;
     for(int i=;i<n;i++){
         scanf("%s",cmd);
         if(cmd[]=='u'){
             scanf("%d",&key);

             st.push(key);
             upDate(key,);
         }else if(cmd[]=='o'){
             if(st.size()==) printf("Invalid\n");
             else{
                 upDate(st.top(),-);
                 printf("%d\n",st.top());
                 st.pop();
             }
         }else if(cmd[]=='e'){
             if(st.size()==) printf("Invalid\n");
             else{
                 printf("%d\n",findMid());
             };
         }
     }
 }

Sample Input:

17
Pop
PeekMedian
Push 3
PeekMedian
Push 2
PeekMedian
Push 1
PeekMedian
Pop
Pop
Push 5
Push 4
PeekMedian
Pop
Pop
Pop
Pop

Sample Output:

Invalid
Invalid
3
2
2
1
2
4
4
5
3
Invalid