C. Sad powers

You're given Q queries of the form (L, R).

For each query you have to find the number of such x that L ≤ x ≤ R and there exist integer numbers a > 0, p > 1 such that x = ap.

Input

The first line contains the number of queries Q (1 ≤ Q ≤ 105).

The next Q lines contains two integers L, R each (1 ≤ L ≤ R ≤ 1018).

Output

Output Q lines — the answers to the queries.

Example

input

Copy

6
1 4
9 9
5 7
12 29
137 591
1 1000000

output

2
1
0
3
17
1111

Note

In query one the suitable numbers are 1 and 4.

提供一种容斥原理的思想。

我们要求不大于n的所有幂数的个数。

把注意力先放在幂这个东西上

ci=pow(n,(1/i))可以得到所有以i为幂，小于等于n的底数的个数

那么最终答案是否是c1+c2+c3+...+ck呢

不是，因为有重复（例如：c2,c3间2^6这个数是被重复计算过的，但我们发现c2,c3的重复的这些数正好是c6）

进一步分析来看，

两个幂数：

ci,cj(i,j均可分解为奇数个不同质数的乘积）间重复的数为ck(k=lcm(i,j)，且k一定可以分解为偶数个不同质数的乘积）

ans=ci+cj-ck

三个幂数：（看图）

ans=ci+cj+ck-c(ij)-c(jk)-c(ik)+c(ijk)

这不就是容斥原理么！！！

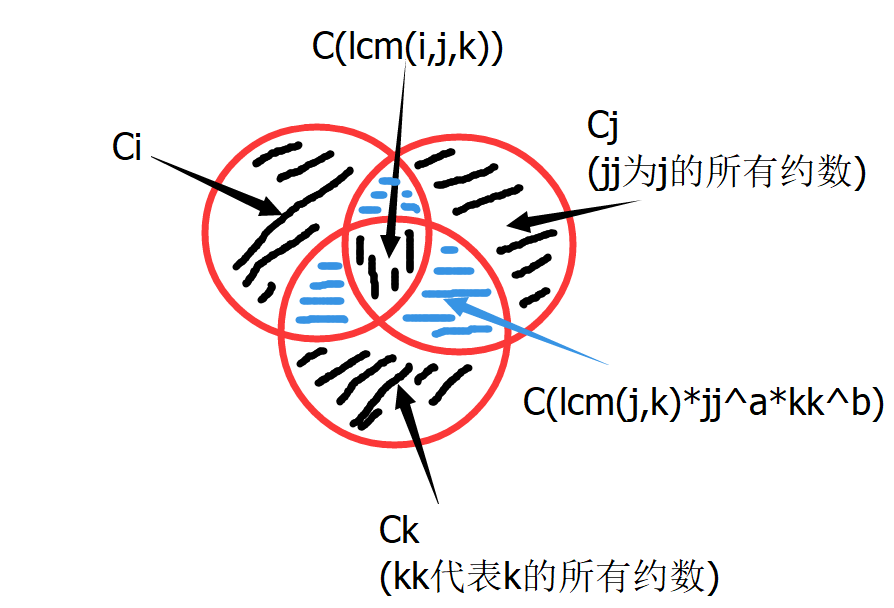
所以具体操作上，先打个容斥表

对象是幂

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double lb;
#define inf 2147483647
const ll INF = 0x3f3f3f3f3f3f3f3fll;
#define ri register int
template <class T> inline T min(T a, T b, T c)
{
    return min(min(a, b), c);
}
template <class T> inline T max(T a, T b, T c)
{
    return max(max(a, b), c);
}
template <class T> inline T min(T a, T b, T c, T d)
{
    return min(min(a, b), min(c, d));
}
template <class T> inline T max(T a, T b, T c, T d)
{
    return max(max(a, b), max(c, d));
}
#define scanf1(x) scanf("%d", &x)
#define scanf2(x, y) scanf("%d%d", &x, &y)
#define scanf3(x, y, z) scanf("%d%d%d", &x, &y, &z)
#define scanf4(x, y, z, X) scanf("%d%d%d%d", &x, &y, &z, &X)
#define pi acos(-1)
#define me(x, y) memset(x, y, sizeof(x));
#define For(i, a, b) for (int i = a; i <= b; i++)
#define FFor(i, a, b) for (int i = a; i >= b; i--)
#define bug printf("***********\n");
#define mp make_pair
#define pb push_back
const int maxn = ;
// name*******************************
int a[];
ll l,r,q;

// function******************************
ll sol(ll x)
{
    ll s=x?:;//大于1就先加上1
    for(ll i=; (1ll<<i)<=x; i++)
        s-=a[i]*((int)pow((lb)x+0.5,(lb)/i)-);//记得减一，1不能参与计数了
    return s;
}
//***************************************
int main()
{
//    ios::sync_with_stdio(0);
//    cin.tie(0);
    // freopen("test.txt", "r", stdin);
    //  freopen("outout.txt","w",stdout);
    a[]=;

    for(int i=; i<=; i++)
        for(int j=i*; j<=; j+=i)
            a[j]-=a[i];
    cin>>q;
    while(q--)
    {
        cin>>l>>r;
        cout<<sol(r)-sol(l-)<<endl;
    }
    return ;
}