概念

凸包(Convex Hull)是一个计算几何（图形学）中的概念。用不严谨的话来讲，给定二维平面上的点集，凸包就是将最外层的点连接起来构成的凸多边型，它能包含点集中所有点的。严谨的定义和相关概念参见维基百科：凸包。

这个算法是由数学大师葛立恒(Graham)发明的，他曾经是美国数学学会(AMS)主席、AT&T首席科学家以及国际杂技师协会(IJA)主席。（太汗了，这位大牛还会玩杂技~）

问题

给定平面上的二维点集，求解其凸包。

过程

1. 在所有点中选取y坐标最小的一点H，当作基点。如果存在多个点的y坐标都为最小值，则选取x坐标最小的一点。坐标相同的点应排除。然后按照其它各点p和基点构成的向量<H,p>与x轴的夹角进行排序，夹角由大至小进行顺时针扫描，反之则进行逆时针扫描。实现中无需求得夹角，只需根据向量的内积公式求出向量的模即可。以下图为例，基点为H，根据夹角由小至大排序后依次为H，K，C，D，L，F，G，E，I，B，A，J。下面进行逆时针扫描。

2. 线段<H, K>一定在凸包上，接着加入C。假设线段<K, C>也在凸包上，因为就H，K，C三点而言，它们的凸包就是由此三点所组成。但是接下来加入D时会发现，线段<K, D>才会在凸包上，所以将线段<K, C>排除，C点不可能是凸包。

3. 即当加入一点时，必须考虑到前面的线段是否会出现在凸包上。从基点开始，凸包上每条相临的线段的旋转方向应该一致，并与扫描的方向相反。如果发现新加的点使得新线段与上线段的旋转方向发生变化，则可判定上一点必然不在凸包上。实现时可用向量叉积进行判断，设新加入的点为pn + 1，上一点为pn，再上一点为pn - 1。顺时针扫描时，如果向量<pn - 1, pn>与<pn, pn + 1>的叉积为正（逆时针扫描判断是否为负），则将上一点删除。删除过程需要回溯，将之前所有叉积符号相反的点都删除，然后将新点加入凸包。

在上图中，加入K点时，由于线段<H,K>相对于<H,C>为顺时针旋转，所以C点不在凸包上，应该删除，保留K点。接着加入D点，由于线段<K, D>相对<H, K>为逆时针旋转，故D点保留。按照上述步骤进行扫描，直到点集中所有的点都遍例完成，即得到凸包。

复杂度

这个算法可以直接在原数据上进行运算，因此空间复杂度为O(1)。但如果将凸包的结果存储到另一数组中，则可能在代码级别进行优化。由于在扫描凸包前要进行排序，因此时间复杂度至少为快速排序的O(nlgn)。后面的扫描过程复杂度为O(n)，因此整个算法的复杂度为O(nlgn)。

C++/STL实现

#include <algorithm>
#include <iostream>
#include <vector>
#include <math.h>
using namespace std;
//二维点(或向量)结构体定义
#ifndef _WINDEF_
struct POINT { int x; int y; };
#endif
typedef vector<POINT> PTARRAY;
//判断两个点(或向量)是否相等
bool operator==(const POINT &pt1, const POINT &pt2) {
    return (pt1.x == pt2.x && pt1.y == pt2.y);
}
// 比较两个向量pt1和pt2分别与x轴向量(1, 0)的夹角
bool CompareVector(const POINT &pt1, const POINT &pt2) {
    //求向量的模
    float m1 = sqrt((float)(pt1.x * pt1.x + pt1.y * pt1.y));
    float m2 = sqrt((float)(pt2.x * pt2.x + pt2.y * pt2.y));
    //两个向量分别与(1, 0)求内积
    float v1 = pt1.x / m1, v2 = pt2.x / m2;
    return (v1 > v2 || (v1 == v2 && m1 < m2));
}
//计算凸包
void CalcConvexHull(PTARRAY &vecSrc) {
    //点集中至少应有3个点，才能构成多边形
    if (vecSrc.size() < 3) {
        return;
    }
    //查找基点
    POINT ptBase = vecSrc.front(); //将第1个点预设为最小点
    for (PTARRAY::iterator i = vecSrc.begin() + 1; i != vecSrc.end(); ++i) {
        //如果当前点的y值小于最小点，或y值相等，x值较小
        if (i->y < ptBase.y || (i->y == ptBase.y && i->x > ptBase.x)) {
            //将当前点作为最小点
            ptBase = *i;
        }
    }
    //计算出各点与基点构成的向量
    for (PTARRAY::iterator i = vecSrc.begin(); i != vecSrc.end();) {
        //排除与基点相同的点，避免后面的排序计算中出现除0错误
        if (*i == ptBase) {
            i = vecSrc.erase(i);
        }
        else {
            //方向由基点到目标点
            i->x -= ptBase.x, i->y -= ptBase.y;
            ++i;
        }
    }
    //按各向量与横坐标之间的夹角排序
    sort(vecSrc.begin(), vecSrc.end(), &CompareVector);
    //删除相同的向量
    vecSrc.erase(unique(vecSrc.begin(), vecSrc.end()), vecSrc.end());
    //计算得到首尾依次相联的向量
    for (PTARRAY::reverse_iterator ri = vecSrc.rbegin();
        ri != vecSrc.rend() - 1; ++ri) {
        PTARRAY::reverse_iterator riNext = ri + 1;
        //向量三角形计算公式
        ri->x -= riNext->x, ri->y -= riNext->y;
    }
    //依次删除不在凸包上的向量
    for (PTARRAY::iterator i = vecSrc.begin() + 1; i != vecSrc.end(); ++i) {
        //回溯删除旋转方向相反的向量，使用外积判断旋转方向
        for (PTARRAY::iterator iLast = i - 1; iLast != vecSrc.begin();) {
            int v1 = i->x * iLast->y, v2 = i->y * iLast->x;
            //如果叉积小于0，则无没有逆向旋转
            //如果叉积等于0，还需判断方向是否相逆
            if (v1 < v2 || (v1 == v2 && i->x * iLast->x > 0 &&
                i->y * iLast->y > 0)) {
                    break;
            }
            //删除前一个向量后，需更新当前向量，与前面的向量首尾相连
            //向量三角形计算公式
            i->x += iLast->x, i->y += iLast->y;
            iLast = (i = vecSrc.erase(iLast)) - 1;
        }
    }
    //将所有首尾相连的向量依次累加，换算成坐标
    vecSrc.front().x += ptBase.x, vecSrc.front().y += ptBase.y;
    for (PTARRAY::iterator i = vecSrc.begin() + 1; i != vecSrc.end(); ++i) {
        i->x += (i - 1)->x, i->y += (i - 1)->y;
    }
    //添加基点，全部的凸包计算完成
    vecSrc.push_back(ptBase);
}
 
int main(void) {
    int nPtCnt = 100; //生成的随机点数
    PTARRAY vecSrc, vecCH;
    for (int i = 0; i < nPtCnt; ++i) {
        POINT ptIn = { rand() % 20, rand() % 20 };
        vecSrc.push_back(ptIn);
        cout << ptIn.x << ", " << ptIn.y << endl;
    }
    CalcConvexHull(vecSrc);
    cout << "\nConvex Hull:\n";
    for (PTARRAY::iterator i = vecSrc.begin(); i != vecSrc.end(); ++i) {
        cout << i->x << ", " << i->y << endl;
    }
    return 0;
}

概念

凸包(Convex Hull)是一个计算几何（图形学）中的概念。用不严谨的话来讲，给定二维平面上的点集，凸包就是将最外层的点连接起来构成的凸多边型，它能包含点集中所有点的。严谨的定义和相关概念参见维基百科：凸包。

这个算法是由数学大师葛立恒(Graham)发明的，他曾经是美国数学学会(AMS)主席、AT&T首席科学家以及国际杂技师协会(IJA)主席。（太汗了，这位大牛还会玩杂技~）

问题

给定平面上的二维点集，求解其凸包。

过程

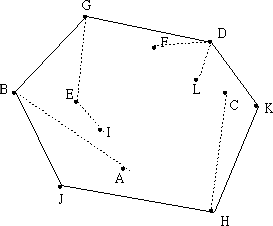
1. 在所有点中选取y坐标最小的一点H，当作基点。如果存在多个点的y坐标都为最小值，则选取x坐标最小的一点。坐标相同的点应排除。然后按照其它各点p和基点构成的向量<H,p>与x轴的夹角进行排序，夹角由大至小进行顺时针扫描，反之则进行逆时针扫描。实现中无需求得夹角，只需根据向量的内积公式求出向量的模即可。以下图为例，基点为H，根据夹角由小至大排序后依次为H，K，C，D，L，F，G，E，I，B，A，J。下面进行逆时针扫描。

2. 线段<H, K>一定在凸包上，接着加入C。假设线段<K, C>也在凸包上，因为就H，K，C三点而言，它们的凸包就是由此三点所组成。但是接下来加入D时会发现，线段<K, D>才会在凸包上，所以将线段<K, C>排除，C点不可能是凸包。

3. 即当加入一点时，必须考虑到前面的线段是否会出现在凸包上。从基点开始，凸包上每条相临的线段的旋转方向应该一致，并与扫描的方向相反。如果发现新加的点使得新线段与上线段的旋转方向发生变化，则可判定上一点必然不在凸包上。实现时可用向量叉积进行判断，设新加入的点为pn + 1，上一点为pn，再上一点为pn - 1。顺时针扫描时，如果向量<pn - 1, pn>与<pn, pn + 1>的叉积为正（逆时针扫描判断是否为负），则将上一点删除。删除过程需要回溯，将之前所有叉积符号相反的点都删除，然后将新点加入凸包。

在上图中，加入K点时，由于线段<H,K>相对于<H,C>为顺时针旋转，所以C点不在凸包上，应该删除，保留K点。接着加入D点，由于线段<K, D>相对<H, K>为逆时针旋转，故D点保留。按照上述步骤进行扫描，直到点集中所有的点都遍例完成，即得到凸包。

复杂度

这个算法可以直接在原数据上进行运算，因此空间复杂度为O(1)。但如果将凸包的结果存储到另一数组中，则可能在代码级别进行优化。由于在扫描凸包前要进行排序，因此时间复杂度至少为快速排序的O(nlgn)。后面的扫描过程复杂度为O(n)，因此整个算法的复杂度为O(nlgn)。

C++/STL实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
#include <algorithm>
#include <iostream>
#include <vector>
#include <math.h>
using namespace std;
//二维点(或向量)结构体定义
#ifndef _WINDEF_
struct POINT { int x; int y; };
#endif
typedef vector<POINT> PTARRAY;
//判断两个点(或向量)是否相等
bool operator==(const POINT &pt1, const POINT &pt2) {
    return (pt1.x == pt2.x && pt1.y == pt2.y);
}
// 比较两个向量pt1和pt2分别与x轴向量(1, 0)的夹角
bool CompareVector(const POINT &pt1, const POINT &pt2) {
    //求向量的模
    float m1 = sqrt((float)(pt1.x * pt1.x + pt1.y * pt1.y));
    float m2 = sqrt((float)(pt2.x * pt2.x + pt2.y * pt2.y));
    //两个向量分别与(1, 0)求内积
    float v1 = pt1.x / m1, v2 = pt2.x / m2;
    return (v1 > v2 || (v1 == v2 && m1 < m2));
}
//计算凸包
void CalcConvexHull(PTARRAY &vecSrc) {
    //点集中至少应有3个点，才能构成多边形
    if (vecSrc.size() < 3) {
        return;
    }
    //查找基点
    POINT ptBase = vecSrc.front(); //将第1个点预设为最小点
    for (PTARRAY::iterator i = vecSrc.begin() + 1; i != vecSrc.end(); ++i) {
        //如果当前点的y值小于最小点，或y值相等，x值较小
        if (i->y < ptBase.y || (i->y == ptBase.y && i->x > ptBase.x)) {
            //将当前点作为最小点
            ptBase = *i;
        }
    }
    //计算出各点与基点构成的向量
    for (PTARRAY::iterator i = vecSrc.begin(); i != vecSrc.end();) {
        //排除与基点相同的点，避免后面的排序计算中出现除0错误
        if (*i == ptBase) {
            i = vecSrc.erase(i);
        }
        else {
            //方向由基点到目标点
            i->x -= ptBase.x, i->y -= ptBase.y;
            ++i;
        }
    }
    //按各向量与横坐标之间的夹角排序
    sort(vecSrc.begin(), vecSrc.end(), &CompareVector);
    //删除相同的向量
    vecSrc.erase(unique(vecSrc.begin(), vecSrc.end()), vecSrc.end());
    //计算得到首尾依次相联的向量
    for (PTARRAY::reverse_iterator ri = vecSrc.rbegin();
        ri != vecSrc.rend() - 1; ++ri) {
        PTARRAY::reverse_iterator riNext = ri + 1;
        //向量三角形计算公式
        ri->x -= riNext->x, ri->y -= riNext->y;
    }
    //依次删除不在凸包上的向量
    for (PTARRAY::iterator i = vecSrc.begin() + 1; i != vecSrc.end(); ++i) {
        //回溯删除旋转方向相反的向量，使用外积判断旋转方向
        for (PTARRAY::iterator iLast = i - 1; iLast != vecSrc.begin();) {
            int v1 = i->x * iLast->y, v2 = i->y * iLast->x;
            //如果叉积小于0，则无没有逆向旋转
            //如果叉积等于0，还需判断方向是否相逆
            if (v1 < v2 || (v1 == v2 && i->x * iLast->x > 0 &&
                i->y * iLast->y > 0)) {
                    break;
            }
            //删除前一个向量后，需更新当前向量，与前面的向量首尾相连
            //向量三角形计算公式
            i->x += iLast->x, i->y += iLast->y;
            iLast = (i = vecSrc.erase(iLast)) - 1;
        }
    }
    //将所有首尾相连的向量依次累加，换算成坐标
    vecSrc.front().x += ptBase.x, vecSrc.front().y += ptBase.y;
    for (PTARRAY::iterator i = vecSrc.begin() + 1; i != vecSrc.end(); ++i) {
        i->x += (i - 1)->x, i->y += (i - 1)->y;
    }
    //添加基点，全部的凸包计算完成
    vecSrc.push_back(ptBase);
}
 
int main(void) {
    int nPtCnt = 100; //生成的随机点数
    PTARRAY vecSrc, vecCH;
    for (int i = 0; i < nPtCnt; ++i) {
        POINT ptIn = { rand() % 20, rand() % 20 };
        vecSrc.push_back(ptIn);
        cout << ptIn.x << ", " << ptIn.y << endl;
    }
    CalcConvexHull(vecSrc);
    cout << "\nConvex Hull:\n";
    for (PTARRAY::iterator i = vecSrc.begin(); i != vecSrc.end(); ++i) {
        cout << i->x << ", " << i->y << endl;
    }
    return 0;
}

Graham's Scan法求解凸包问题的更多相关文章

  1. 【计算几何】二维凸包——Graham's Scan法

    凸包 点集Q的凸包(convex hull)是指一个最小凸多边形,满足Q中的点或者在多边形边上或者在其内.右图中由红色线段表示的多边形就是点集Q={p0,p1,...p12}的凸包. 一组平面上的点, ...

  2. Scan法求凸包

    题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1348 给一个半径和n个点 求圆的周长 + n个点的凸包的周长 #include<bits/std ...

  3. 计算几何---凸包问题（Graham/Andrew Scan ）

    概念 凸包(Convex Hull)是一个计算几何(图形学)中的概念.用不严谨的话来讲,给定二维平面上的点集,凸包就是将最外层的点连接起来构成的凸多边型,它能包含点集中所有点的.严谨的定义和相关概念参 ...

  4. 破圈法求解最小生成树c语言实现（已验证）

    破圈法求解最小生成树c语言实现(已验证) 下面是算法伪代码,每一个算法都取一个图作为输入,并返回一个边集T. 对该算法,证明T是一棵最小生成树,或者证明T不是一棵最小生成树.此外,对于每个算法,无论它 ...

  5. POJ 1061 青蛙的约会（拓展欧几里得算法求解模线性方程组详解）

    题目链接: BZOJ: https://www.lydsy.com/JudgeOnline/problem.php?id=1477 POJ: https://cn.vjudge.net/problem ...

  6. Coursera在线学习---第一节.梯度下降法与正规方程法求解模型参数比较

    一.梯度下降法 优点:即使特征变量的维度n很大,该方法依然很有效 缺点:1)需要选择学习速率α 2)需要多次迭代 二.正规方程法(Normal Equation) 该方法可以一次性求解参数Θ 优点:1 ...

  7. 逆波兰法求解数学表达示（C++）

    主要是栈的应用,里面有两个函数deleteSpace(),stringToDouble()在我还有一篇博客其中:对string的一些扩展函数. 本程序仅仅是主要的功能实现,没有差错控制. #inclu ...

  8. 0-1背包问题——回溯法求解【Python】

    回溯法求解0-1背包问题: 问题:背包大小 w,物品个数 n,每个物品的重量与价值分别对应 w[i] 与 v[i],求放入背包中物品的总价值最大. 回溯法核心:能进则进,进不了则换,换不了则退.(按照 ...

  9. poj 2079(旋转卡壳求解凸包内最大三角形面积)

    Triangle Time Limit: 3000MS   Memory Limit: 30000K Total Submissions: 9060   Accepted: 2698 Descript ...

随机推荐

  1. python中安装Tensorflow

    执行命令:pip install --upgrade tensorflow 即可.

  2. 【LeetCode5】Longest Palindromic Substring★★

    1.题目描述: 2.解题思路: 题意:求一个字符串的最长回文子串. 方法一:中心扩展法.遍历字符串的每一个字符,如果存在回文子串,那么中心是某一个字符(奇数)或两个字符的空隙(偶数),然后分两种情况( ...

  3. python基础1之python介绍、安装、变量和字符编码、数据类型、输入输出、数据运算、循环

    开启python之路 内容概要: 一.python介绍 二.安装 三.第一个python程序 四.变量和字符编码 五.用户输入 六.数据类型 七.一切皆对象 八.数据运算 九.if else 流程判断 ...

  4. 使用HibernateDaoSupport抽取BaseDao

            在开发采用Struts2+Spring+hibernate这三大框架的项目时,我们需要一个抽取一个BaseDao.这个Dao里面CRUD都给封装好,后续的其他Dao直接用它的功能就可以 ...

  5. Python+Matplotlib制作动画

    注: 在"实验设计与数据处理"的课后作业中,有一个数据可视化的作业,利用课程上学习的某种方法找一个二维函数的最大值,并将这个寻找的过程可视化.在作业里面利用了Matplotlib的 ...

  6. Centos 发送smtp邮件

    说明:          1.本文是用网易smtp服务,QQ的没试过        2.在Centos7上测试 实现:        1.关闭本机的sendmail服务或者postfix服务     ...

  7. 【Android UI设计与开发】第01期：引导界面（一）ViewPager介绍和使用详解

    做Android开发加起来差不多也有一年多的时间了,总是想写点自己在开发中的心得体会与大家一起交流分享.共同进步,刚开始写也不知该如何下手,仔细想了一下,既然是刚开始写,那就从一个软件给人最直观的感受 ...

  8. Jq_input file标签上传图片到服务器

    引入jQuery库引入ajaxfileupload.js上传插件库(这也是jQuery的一个插件)以ASP.NET为例 <input type="file" id=" ...

  9. Linux删除多余内核

    查看已安装内核 sudo dpkg --get-selections |grep linux-image 查看当前内核 uname -r 卸载内核 sudo apt-get remove 内核名称 配 ...

  10. Unity 3D 简易制作摄像机围绕物体随鼠标旋转效果

    Unity 3D 简易制作摄像机围绕物体随鼠标旋转效果 梗概: 一. 摄像机围绕目标物体旋转, 即摄像机离目标物体有一定的距离且旋转轴心为该物体的位置. 二. 当目标物体被障碍物挡住后, 需要将摄像机 ...