[机器学习&数据挖掘]SVM---核函数
1、核函数概述:
核函数通俗的来说是通过一个函数将向量的低维空间映射到一个高维空间,从而将低维空间的非线性问题转换为高维空间的线性问题来求解,从而再利用之前说的一系列线性支持向量机,常用的核函数如下:
多项式核函数:
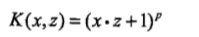
高斯核函数:
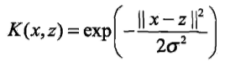
比如硬间隔种的目标函数为:

而核函数替换后的目标函数为:
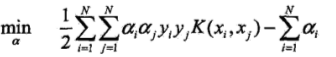
从这个两个目标函数找共同点,其实会发现核函数是作用在特征向量上,开始的目标函数一次计算是利用了两个特征向量,而接下来的核函数是对两个特征向量做函数运算,假如将核函数利用在一次运算利用三个特征向量的计算,这时核函数就会对这三个特征向量做核函数,其实就是一个替换的问题,将两个特征向量点积运算换成一个核函数的值,仅此而已。
2、SMO算法概述:
因此接下来的处理还是求解拉格朗日乘子、w、b,因此引入SMO(序列最小最优化算法)
首先SMO算法要解决的对偶问题如下:

SMO算法是一种启发式算法,基本思路:如果所有变量的解都满足此最优化问题的KKT条件,那么这个最优化的问题的解就得到了,SMO算法其实就是在求解拉格朗日算子。SMO算法子问题:先选择两个变量,然后固定其他变量,针对此两个变量构建二次规划问题,子问题由两个变量,一个是违反KKT条件最严重的变量,另一个由约束条件自动确定,然后对此子问题求解,当此两个变量都满足KKT条件,则子问题求解完成。SMO算法就是将问题不断的分解为此子问题,直到所有的变量的解都满足此问题的KKT条件,从而结束算法
通过以上的对偶问题可以将子问题写成(此处假定选择两个变量alpha1、alpha2):
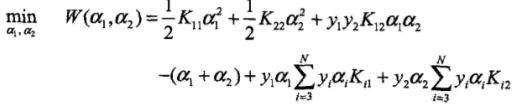

注意:此子问题的目标函数是从上面的对偶问题得来,在推导的过程中会发现有一些项没有,是因为这个时候只有alpha1和alpha2是变量,其他的都看作固定的值,就类似求min(f(x))和min(f(x)+C)的解x是一样的(C为常数)
3、alpha计算公式:
接下来几个公式用于每次计算:
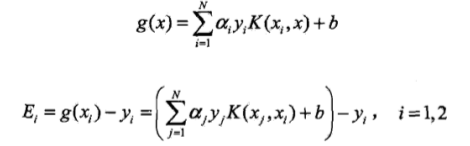
注:Ei是g(x)对xi的预测值对yi的值之差
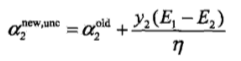
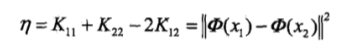
此计算的是alpha2未经过处理的值,因为各个alpha都由一个范围的,具体如下分段函数:

通过alpha2可以求得alpha1的新值如下:
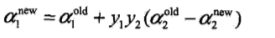
4、变量选择:
(1)首先面临的是第一个变量的选择,在SMO算法的概述中我也介绍过,就是最不满足此问题的KKT条件,KKT条件为何看如下(KKT是相对于每个样本点来说的即(xi,yi)):
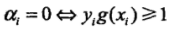
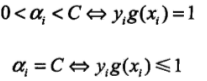 g(xi)如上述的式子
g(xi)如上述的式子
第一个变量的选择是SMO的外层循环,在检验过程中,首先遍历所有满足0<alpha<C条件的样本点,即在间隔边界上的支持向量点,检验其是否满足KKT条件,如果都满足,则遍历整个训练集是否满足KKT条件,选择最不满足的点为第一个变量。
(2)其次是第二个变量的选择:第二个变量的选择是SMO的内层循环,首先假定已经选定了第一个变量,第二个变量的选择是希望能使alpha2有足够大的变化,一种简单的做法是其对应的|E1-E2|最大。在特殊的情况下,通过以上方法不能使目标函数有足够的下降,则采用向下启发规则继续选择alpha2,遍历所有的间隔边界上的支持向量点,依次将其作为alpha2试用,直到目标函数有足够的下降,若找不到则便利整个训练集;若仍找不到,则放弃alpha1,通过外层循环继续选择另外的alpha1.
(3)计算b和差值Ei
因为在每次完成两个变量的优化之后,都需要重新计算b和Ei,主要是Ei的计算需要用的b,公式如下:


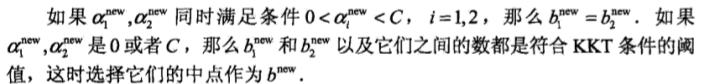
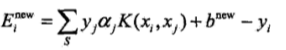
[机器学习&数据挖掘]SVM---核函数的更多相关文章
- 【机器学习】SVM核函数
知识预备 1. 回顾:logistic回归出发,引出了SVM,即支持向量机[续]. 2. Mercer定理:如果函数K是上的映射(也就是从两个n维向量映射到实数域).那么如果K是一个有效核函数(也称 ...
- 机器学习:SVM(核函数、高斯核函数RBF)
一.核函数(Kernel Function) 1)格式 K(x, y):表示样本 x 和 y,添加多项式特征得到新的样本 x'.y',K(x, y) 就是返回新的样本经过计算得到的值: 在 SVM 类 ...
- 机器学习&数据挖掘笔记_16(常见面试之机器学习算法思想简单梳理)
前言: 找工作时(IT行业),除了常见的软件开发以外,机器学习岗位也可以当作是一个选择,不少计算机方向的研究生都会接触这个,如果你的研究方向是机器学习/数据挖掘之类,且又对其非常感兴趣的话,可以考虑考 ...
- 机器学习&数据挖掘笔记(常见面试之机器学习算法思想简单梳理)
机器学习&数据挖掘笔记_16(常见面试之机器学习算法思想简单梳理) 作者:tornadomeet 出处:http://www.cnblogs.com/tornadomeet 前言: 找工作时( ...
- 常用的机器学习&数据挖掘知识点【转】
转自: [基础]常用的机器学习&数据挖掘知识点 Basis(基础): MSE(Mean Square Error 均方误差),LMS(LeastMean Square 最小均方),LSM(Le ...
- [转]机器学习&数据挖掘笔记_16(常见面试之机器学习算法思想简单梳理)
机器学习&数据挖掘笔记_16(常见面试之机器学习算法思想简单梳理) 转自http://www.cnblogs.com/tornadomeet/p/3395593.html 前言: 找工作时(I ...
- 常见的机器学习&数据挖掘知识点
原文:http://blog.csdn.net/heyongluoyao8/article/details/47840255 常见的机器学习&数据挖掘知识点 转载请说明出处 Basis(基础) ...
- 机器学习四 SVM
目录 引言 SVM 线性可分SVM 线性不可分SVM Hinge Loss 非线性SVM 核函数 总结 参考文献 引言 在深度神经网终(Deep Neural Network, DNN) 大热之前, ...
- Python 网页爬虫 & 文本处理 & 科学计算 & 机器学习 & 数据挖掘兵器谱(转)
原文:http://www.52nlp.cn/python-网页爬虫-文本处理-科学计算-机器学习-数据挖掘 曾经因为NLTK的缘故开始学习Python,之后渐渐成为我工作中的第一辅助脚本语言,虽然开 ...
- [resource-]Python 网页爬虫 & 文本处理 & 科学计算 & 机器学习 & 数据挖掘兵器谱
reference: http://www.52nlp.cn/python-%e7%bd%91%e9%a1%b5%e7%88%ac%e8%99%ab-%e6%96%87%e6%9c%ac%e5%a4% ...
随机推荐
- 阿里云ECS服务器源配置
前段时间领取了阿里云ECS免费试用6个月的福利,此处记录一下服务器源配置过程和服务器用户创建过程. 一.CentOS源配置 1.备份 mv /etc/yum.repos.d/CentOS-Base.r ...
- 20135202闫佳歆--week5 系统调用(下)--学习笔记
此为个人笔记存档 week 5 系统调用(下) 一.给MenuOS增加time和time-asm命令 这里老师示范的时候是已经做好的了: rm menu -rf 强制删除 git clone http ...
- Linux内核读书笔记第二周
什么是系统调用 简单来说,系统调用就是用户程序和硬件设备之间的桥梁.用户程序在需要的时候,通过系统调用来使用硬件设备. 系统调用的存在,有以下重要的意义: 1)用户程序通过系统调用来使用硬件,而不用关 ...
- Alpha 答辩总结
前言 作业发布 组长 成员 贡献比例 ★ 530 雨勤 23% 311 旭 23% 403 俊 18% 223 元 23% 437 海辉 13% 10天 Alpha 冲刺站立会议博客链接汇总 Alph ...
- 正则的replace函数传参使用
<script> var str = "a1ba2b"; var reg = /a.b/g; str = str.replace(reg,function(a,b){ ...
- ORM的详解
有很多小伙伴都不太理解ORM是什么,其实不用想象的那么复杂.我们先根据3W1H去理解. who:首先ORM可以立即为(Object/Relation Mapping): 对象/关系映射 what:其次 ...
- USACO 2012 December ZQUOJ 24128 Wifi Setup(动态dp)
题意:给出在同一条直线上的n个点和两个数A,B,现在要在这条直线上放置若干个信号塔,每个信号塔有一个r值,假设它的位置是x,则它能覆盖的范围是x-r~x+r,放置一个信号塔的花费是A+B*r,问要覆盖 ...
- element-ui upload组建上传 file-list踩过的坑
昨天修完了一个上传组件删除时,图片删掉了,但是地址仍然在的bug,今天测试告诉我bug没休掉,what !,昨天修完之后我自测了一下,OK的好吗,但是测试给我演示了一下,问题仍然存在!!!我看了一下调 ...
- 【大数据】Zookeeper学习笔记
第1章 Zookeeper入门 1.1 概述 Zookeeper是一个开源的分布式的,为分布式应用提供协调服务的Apache项目. 1.2 特点 1.3 数据结构 1.4 应用场景 提供的服务包括:统 ...
- C# DataTable Select用法
DataRow[] dr = ds.Tables[0].Select("列名='该列你要查询的值'"); DataRow[] dr = ds.Tables[0].Select(&q ...
