数据结构笔记之跳表(SkipList)
一、跳表简述
跳表可以看做是一个带有索引的链表,在介绍跳表之前先看一下一个普通的链表,假如当前维护了一个有序的链表:

现在要在这个链表中查找128,因为事先不知道链表中数值的分布情况,我们只能从前到后依次遍历,那么有没有什么取巧的方法呢?
如果我们能够存储下最中间节点的引用,比如存储节点29的引用,然后每次要查找节点的时候就先跟29比较一下,如果比29小就还是从前往后找(因为不会超过中间节点,从前往后和从中间往前区别不大),如果比29大就直接跳到29开始往后找,这种思想就是为链表添加了一个简单的索引,一下可以节省掉一半的查找时间。跳表的设计思想类似,通过为链表的每个节点设置高度来添加索引,不同的高度称为不同的层,每一层的next只能指向当前层的下一个节点,下面是一个跳表的示例:
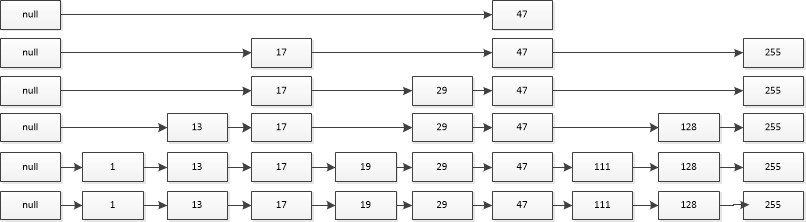
最左面一列null为head节点,用于保存每一层的第一个节点,在查找的时候先从最高层开始查找,比如要在上面的跳表中查找128:
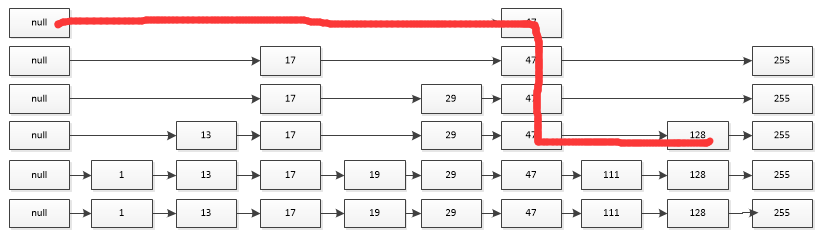
首先取最高层第六层的next,是47,比128小,直接跳到47,然后47的第六层的next是null,说明到了最后一个了,层数减少,47的第五层的next是255,比128大,也不行,继续减少层数,47的第四层的next是255,依然比128大,继续减少层数,47的第三层的next是128,get it!
看上面的过程有没有意识到一个问题,就是如果跳表的层数过多的话”比较-降层“这个过程就会有不少的浪费,比如上面的在47这个节点进行了4次比较才找到了有效的next节点,如果这个值再大一点的话就会退化得很严重。那么这个层是如何来的呢,跳表的高度是通过一个随机数决定的,初始时默认为一层,然后一直产生随机数只要小于0.5就将层数加一层继续随机,但是随机这种东西毕竟是不可控的,为了避免出现过高的层数最好还是设置一个最大层数以免某些节点的层数过大。
二、跳表的实现
跳表的简单Java实现:
SkipList.java:
package alg.link; import org.apache.commons.lang3.StringUtils; /**
* 跳表结构的简单Java实现
*
* @author CC11001100
*/
public class SkipList<T extends Comparable<T>> { private static final double DEFAULT_CONTINUE_INCREMENT_LEVEL_THRESHOLD = 0.75;
private static final int DEFAULT_MAX_LEVEL = 10; // 用于控制层数,决定层数时当随机数小于此值时会一直升层直到最大,取值范围[0, 1],值越大越可能得到高层数,此值设置不当很有可能退化成链表
private double continueIncrementLevelThreshold;
// 为了防止随机数出现异常情况过高,对最大层数做一个限制
private int maxLevel;
// 链表的头结点,每一层的头都保存在这里
private Node<T> head; public SkipList() {
this(DEFAULT_CONTINUE_INCREMENT_LEVEL_THRESHOLD, DEFAULT_MAX_LEVEL);
} public SkipList(double threshold) {
this(threshold, DEFAULT_MAX_LEVEL);
} public SkipList(double threshold, int maxLevel) {
this.continueIncrementLevelThreshold = threshold;
this.maxLevel = maxLevel;
this.head = new Node<>(null, 0);
// 初始化时就将其扩充到最大避免后面扩容增加复杂性,只有head会浪费一些空间其它节点都是有几层申请多长的数组
this.head.next = new Node[maxLevel];
} public void add(T value) {
Node[] previous = findPrevious(value);
Node<T> node = new Node<>(value, randomLevel());
for (int i = 0; i < previous.length && i < node.level; i++) {
node.next[i] = previous[i].next[i];
previous[i].next[i] = node;
}
if (node.level > head.level) {
for (int i = node.level - 1; i >= 0 && head.next[i] == null; i--) {
head.next[i] = node;
}
head.level = node.level;
}
} public void remove(T value) {
Node[] previous = findPrevious(value);
Node node = previous[0].next[0];
if (node.value.compareTo(value) != 0) {
return;
}
for (int i = 0; i < previous.length && i < node.level; i++) {
previous[i].next[i] = node.next[i];
}
} public boolean contains(T value) {
Node[] previous = findPrevious(value);
Node node = previous[0].next[0];
return node.value.compareTo(value) == 0;
} private int randomLevel() {
int level = 1;
while (level < maxLevel && Math.random() < continueIncrementLevelThreshold) {
level++;
}
return level;
} private Node[] findPrevious(T value) {
Node[] previous = new Node[head.level];
Node<T> node = head;
for (int i = head.level - 1; i >= 0; i--) {
while (node.next[i] != null && node.next[i].value.compareTo(value) < 0) {
node = node.next[i];
}
previous[i] = node;
}
return previous;
} /**
* head_next level_next # 注释,实际不会打印标题
* 67 67
* 67 67
* 67 67
* 67 67
* 19 19 67
* 19 19 67
* 6 6 19 67
* 6 6 19 67 82
* 6 6 19 46 67 82
*/
public void show() {
StringBuilder sb = new StringBuilder();
for (int i = maxLevel; i > 0; i--) {
// 这一层级的头指针指向谁
Node levelHead = head.next[i - 1];
if (levelHead != null) {
sb.append(String.format("%-10s", levelHead.value.toString())).append("\t");
} else {
sb.append(StringUtils.repeat(" ", 10)).append("\t");
}
// 然后是每一层按层数是否出现打印value或空白填充
Node node = head.next[0];
while (node != null) {
String s = node.value.toString();
if (node.level >= i) {
sb.append(s).append("\t");
} else {
sb.append(StringUtils.repeat(" ", s.length())).append("\t");
}
node = node.next[0];
}
if (i != 1) {
sb.append("\n");
}
}
System.out.println(sb.toString());
} private static class Node<T extends Comparable<T>> {
// 当前节点的值
T value;
// 当前节点的层数
int level;
// 记录当前节点在每一层的next节点
Node<T>[] next; private Node(T value, int level) {
this.value = value;
this.level = level;
this.next = new Node[level];
}
} }
SkipListTest.java:
package alg.link; import java.util.ArrayList;
import java.util.List;
import java.util.Random; /**
* @author CC11001100
*/
public class SkipListTest { public static void main(String[] args) { SkipList<Integer> skipList = new SkipList<>();
Random random = new Random();
List<Integer> numList = new ArrayList<>();
for (int i = 0; i < 30; i++) {
int n = random.nextInt(100);
System.out.println("now insert " + n);
skipList.add(n);
skipList.show();
numList.add(n);
System.out.println("---------------------------------------------------------------------------"); if (Math.random() < 0.5 && !numList.isEmpty()) {
int removeNum = numList.remove(random.nextInt(numList.size()));
System.out.println("now remove " + removeNum);
skipList.remove(removeNum);
skipList.show();
System.out.println("---------------------------------------------------------------------------");
}
} } }
测试效果:
now insert 35 35 35
35 35
35 35
---------------------------------------------------------------------------
now insert 56
56 56
56 56
56 56
56 56
56 56
56 56
56 56
35 35 56
35 35 56
35 35 56
---------------------------------------------------------------------------
now remove 35
56 56
56 56
56 56
56 56
56 56
56 56
56 56
56 56
56 56
56 56
---------------------------------------------------------------------------
now insert 45
56 56
56 56
56 56
56 56
56 56
45 45 56
45 45 56
45 45 56
45 45 56
45 45 56
---------------------------------------------------------------------------
now remove 56 45 45
45 45
45 45
45 45
45 45
---------------------------------------------------------------------------
now insert 7 45 45
45 45
45 45
45 45
7 7 45
---------------------------------------------------------------------------
now insert 57 45 45
45 45
45 45
45 45 57
7 7 45 57
---------------------------------------------------------------------------
now remove 7 45 45
45 45
45 45
45 45 57
45 45 57
---------------------------------------------------------------------------
now insert 75 45 45
45 45
45 45
45 45 57
45 45 57 75
---------------------------------------------------------------------------
now remove 75 45 45
45 45
45 45
45 45 57
45 45 57
---------------------------------------------------------------------------
now insert 96 45 45
45 45 96
45 45 96
45 45 57 96
45 45 57 96
---------------------------------------------------------------------------
now remove 96 45 45
45 45
45 45
45 45 57
45 45 57
---------------------------------------------------------------------------
now insert 40
40 40
40 40
40 40
40 40
40 40
40 40 45
40 40 45
40 40 45
40 40 45 57
40 40 45 57
---------------------------------------------------------------------------
now remove 40 45 45
45 45
45 45
45 45 57
45 45 57
---------------------------------------------------------------------------
now insert 69 45 45
45 45
45 45 69
45 45 57 69
45 45 57 69
---------------------------------------------------------------------------
now insert 11 45 45
11 11 45
11 11 45 69
11 11 45 57 69
11 11 45 57 69
---------------------------------------------------------------------------
now insert 19 45 45
11 11 45
11 11 45 69
11 11 19 45 57 69
11 11 19 45 57 69
---------------------------------------------------------------------------
now insert 55 45 45
11 11 45
11 11 45 55 69
11 11 19 45 55 57 69
11 11 19 45 55 57 69
---------------------------------------------------------------------------
now remove 55 45 45
11 11 45
11 11 45 69
11 11 19 45 57 69
11 11 19 45 57 69
---------------------------------------------------------------------------
now insert 43 45 45
11 11 45
11 11 45 69
11 11 19 45 57 69
11 11 19 43 45 57 69
---------------------------------------------------------------------------
now remove 43 45 45
11 11 45
11 11 45 69
11 11 19 45 57 69
11 11 19 45 57 69
---------------------------------------------------------------------------
now insert 5 45 45
11 11 45
11 11 45 69
11 11 19 45 57 69
5 5 11 19 45 57 69
---------------------------------------------------------------------------
now remove 5 45 45
11 11 45
11 11 45 69
11 11 19 45 57 69
11 11 19 45 57 69
---------------------------------------------------------------------------
now insert 92 45 45
11 11 45
11 11 45 69
11 11 19 45 57 69 92
11 11 19 45 57 69 92
---------------------------------------------------------------------------
now remove 45 11 11
11 11 69
11 11 19 57 69 92
11 11 19 57 69 92
---------------------------------------------------------------------------
now insert 56 11 11
11 11 69
11 11 19 57 69 92
11 11 19 56 57 69 92
---------------------------------------------------------------------------
now insert 31 11 11
11 11 69
11 11 19 31 57 69 92
11 11 19 31 56 57 69 92
---------------------------------------------------------------------------
now insert 29 11 11
11 11 29 69
11 11 19 29 31 57 69 92
11 11 19 29 31 56 57 69 92
---------------------------------------------------------------------------
now insert 96 11 11 96
11 11 29 69 96
11 11 19 29 31 57 69 92 96
11 11 19 29 31 56 57 69 92 96
---------------------------------------------------------------------------
now insert 0 11 11 96
0 0 11 29 69 96
0 0 11 19 29 31 57 69 92 96
0 0 11 19 29 31 56 57 69 92 96
---------------------------------------------------------------------------
now remove 19 11 11 96
0 0 11 29 69 96
0 0 11 29 31 57 69 92 96
0 0 11 29 31 56 57 69 92 96
---------------------------------------------------------------------------
now insert 54 11 11 54 96
0 0 11 29 54 69 96
0 0 11 29 31 54 57 69 92 96
0 0 11 29 31 54 56 57 69 92 96
---------------------------------------------------------------------------
now insert 8 11 11 54 96
0 0 11 29 54 69 96
0 0 11 29 31 54 57 69 92 96
0 0 8 11 29 31 54 56 57 69 92 96
---------------------------------------------------------------------------
now remove 56 11 11 54 96
0 0 11 29 54 69 96
0 0 11 29 31 54 57 69 92 96
0 0 8 11 29 31 54 57 69 92 96
---------------------------------------------------------------------------
now insert 60 11 11 54 96
0 0 11 29 54 69 96
0 0 11 29 31 54 57 69 92 96
0 0 8 11 29 31 54 57 60 69 92 96
---------------------------------------------------------------------------
now insert 41 41 41
11 11 41 54 96
0 0 11 29 41 54 69 96
0 0 11 29 31 41 54 57 69 92 96
0 0 8 11 29 31 41 54 57 60 69 92 96
---------------------------------------------------------------------------
now remove 92 41 41
11 11 41 54 96
0 0 11 29 41 54 69 96
0 0 11 29 31 41 54 57 69 96
0 0 8 11 29 31 41 54 57 60 69 96
---------------------------------------------------------------------------
now insert 20 41 41
11 11 20 41 54 96
0 0 11 20 29 41 54 69 96
0 0 11 20 29 31 41 54 57 69 96
0 0 8 11 20 29 31 41 54 57 60 69 96
---------------------------------------------------------------------------
now remove 41 11 11 20 54 96
0 0 11 20 29 54 69 96
0 0 11 20 29 31 54 57 69 96
0 0 8 11 20 29 31 54 57 60 69 96
---------------------------------------------------------------------------
now insert 58 11 11 20 54 96
0 0 11 20 29 54 58 69 96
0 0 11 20 29 31 54 57 58 69 96
0 0 8 11 20 29 31 54 57 58 60 69 96
---------------------------------------------------------------------------
now remove 31 11 11 20 54 96
0 0 11 20 29 54 58 69 96
0 0 11 20 29 54 57 58 69 96
0 0 8 11 20 29 54 57 58 60 69 96
---------------------------------------------------------------------------
now insert 79 11 11 20 54 96
0 0 11 20 29 54 58 69 96
0 0 11 20 29 54 57 58 69 79 96
0 0 8 11 20 29 54 57 58 60 69 79 96
---------------------------------------------------------------------------
now insert 38 11 11 20 54 96
0 0 11 20 29 54 58 69 96
0 0 11 20 29 38 54 57 58 69 79 96
0 0 8 11 20 29 38 54 57 58 60 69 79 96
---------------------------------------------------------------------------
now insert 31 11 11 20 54 96
0 0 11 20 29 54 58 69 96
0 0 11 20 29 31 38 54 57 58 69 79 96
0 0 8 11 20 29 31 38 54 57 58 60 69 79 96
---------------------------------------------------------------------------
now remove 79 11 11 20 54 96
0 0 11 20 29 54 58 69 96
0 0 11 20 29 31 38 54 57 58 69 96
0 0 8 11 20 29 31 38 54 57 58 60 69 96
---------------------------------------------------------------------------
now insert 78 11 11 20 54 78 96
0 0 11 20 29 54 58 69 78 96
0 0 11 20 29 31 38 54 57 58 69 78 96
0 0 8 11 20 29 31 38 54 57 58 60 69 78 96
---------------------------------------------------------------------------
now remove 0 11 11 20 54 78 96
11 11 20 29 54 58 69 78 96
11 11 20 29 31 38 54 57 58 69 78 96
8 8 11 20 29 31 38 54 57 58 60 69 78 96
---------------------------------------------------------------------------
.
数据结构笔记之跳表(SkipList)的更多相关文章
- 存储系统的基本数据结构之一: 跳表 (SkipList)
在接下来的系列文章中,我们将介绍一系列应用于存储以及IO子系统的数据结构.这些数据结构相互关联又有着巨大的区别,希望我们能够不辱使命的将他们分门别类的介绍清楚.本文为第一节,介绍一个简单而又有用的数据 ...
- 跳表SkipList
原文:http://www.cnblogs.com/xuqiang/archive/2011/05/22/2053516.html 跳表SkipList 1.聊一聊跳表作者的其人其事 2. 言归正 ...
- C语言跳表(skiplist)实现
一.简介 跳表(skiplist)是一个非常优秀的数据结构,实现简单,插入.删除.查找的复杂度均为O(logN).LevelDB的核心数据结构是用跳表实现的,redis的sorted set数据结构也 ...
- 跳表 SkipList
跳表是平衡树的一种替代的数据结构,和红黑树不同,跳表对树的平衡的实现是基于一种随机化的算法,这样就使得跳表的插入和删除的工作比较简单. 跳表是一种复杂的链表,在简单链表的节点信息之上又增加了额 ...
- 3.3.7 跳表 SkipList
一.前言 concurrentHashMap与ConcurrentSkipListMap性能测试 在4线程1.6万数据的条件下,ConcurrentHashMap 存取速度是ConcurrentSki ...
- 跳表(SkipList)设计与实现(Java)
微信搜一搜「bigsai」关注这个有趣的程序员 文章已收录在 我的Github bigsai-algorithm 欢迎star 前言 跳表是面试常问的一种数据结构,它在很多中间件和语言中得到应用,我们 ...
- [转载] 跳表SkipList
原文: http://www.cnblogs.com/xuqiang/archive/2011/05/22/2053516.html leveldb中memtable的思想本质上是一个skiplist ...
- 跳表(SkipList)原理篇
1.什么是跳表? 维基百科:跳表是一种数据结构.它使得包含n个元素的有序序列的查找和插入操作的平均时间复杂度都是 O(logn),优于数组的 O(n)复杂度.快速的查询效果是通过维护一个多层次的链表实 ...
- 跳表(skiplist)Python实现
# coding=utf-8 # 跳表的Python实现 import random # 最高层数设置为4 MAX_LEVEL = 4 def randomLevel(): ""& ...
随机推荐
- LeetCode 463. Island Perimeter岛屿的周长 (C++)
题目: You are given a map in form of a two-dimensional integer grid where 1 represents land and 0 repr ...
- Day Four
站立式会议 站立式会议内容总结 442 今天:整合主页两个部分的逻辑代码,主页及其跳转基本完成 遇到的问题:无 明天:阅读图书界面逻辑部分完成 331 今天:学习java反射添加类数据到数据库 遇到问 ...
- TAC队--团队选题报告
The Art of Code--团队选题报告 一个APP项目能否被大众所接受,能否拥有受众,the most important是它的idea. 一个好的idea可以为项目带来巨大的改变 一个 独特 ...
- Linux版本CentOS、Ubuntu和Debian的异同
Linux有非常多的发行版本,从性质上划分,大体分为由商业公司维护的商业版本与由开源社区维护的免费发行版本. 商业版本以Redhat为代表,开源社区版本则以debian为代表. #Ubuntu系统 U ...
- Codeforces914G Sum the Fibonacci(FWT)
FWT大杂烩.跟着模拟做很多次FWT即可. #include<iostream> #include<cstdio> #include<cmath> #include ...
- poj 2299 Ultra-QuickSort(树状数组)
Ultra-QuickSort Time Limit: 7000MS Memory Limit: 65536K Total Submissions: 67681 Accepted: 25345 ...
- 使用Ubuntu的Crontab定时任务需要注意的地方
Ubuntu使用crontab定时任务 网上有很多教程,现在记录下我遇到的一些问题,需要注意的地方: 1.定时任务的日志存放路径 网上的说法:cron的日志存放在 /var/log/cron 里面 ...
- Spring Boot -Shiro配置多Realm
核心类简介 xxxToken:用户凭证 xxxFilter:生产token,设置登录成功,登录失败处理方法,判断是否登录连接等 xxxRealm:依据配置的支持Token来认证用户信息,授权用户权限 ...
- 自学huawei之路-AC6005-8AP添加授权码
返回自学Huawei之路 自学huawei之路-AC6005-8AP添加授权码
- 【转】Altium Designer 3D封装下载及导入教程
首先 先晒几个图:是不是很逼真啊.. ---------------------------------------教程---------------------------------------- ...
