POJ3694(KB9-D 割边+LCA)

Network

Time Limit: 5000MS		Memory Limit: 65536K
Total Submissions: 10371		Accepted: 3853

Description

A network administrator manages a large network. The network consists of N computers and M links between pairs of computers. Any pair of computers are connected directly or indirectly by successive links, so data can be transformed between any two computers. The administrator finds that some links are vital to the network, because failure of any one of them can cause that data can't be transformed between some computers. He call such a link a bridge. He is planning to add some new links one by one to eliminate all bridges.

You are to help the administrator by reporting the number of bridges in the network after each new link is added.

Input

The input consists of multiple test cases. Each test case starts with a line containing two integers N(1 ≤ N ≤ 100,000) and M(N - 1 ≤ M ≤ 200,000).
Each of the following M lines contains two integers A and B ( 1≤ A ≠ B ≤ N), which indicates a link between computer A and B. Computers are numbered from 1 to N. It is guaranteed that any two computers are connected in the initial network.
The next line contains a single integer Q ( 1 ≤ Q ≤ 1,000), which is the number of new links the administrator plans to add to the network one by one.
The i-th line of the following Q lines contains two integer A and B (1 ≤ A ≠ B ≤ N), which is the i-th added new link connecting computer A and B.

The last test case is followed by a line containing two zeros.

Output

For each test case, print a line containing the test case number( beginning with 1) and Q lines, the i-th of which contains a integer indicating the number of bridges in the network after the first i new links are added. Print a blank line after the output for each test case.

Sample Input

3 2
1 2
2 3
2
1 2
1 3
4 4
1 2
2 1
2 3
1 4
2
1 2
3 4
0 0

Sample Output

Case 1:
1
0

Case 2:
2
0

Source

2008 Asia Hefei Regional Contest Online by USTC

 

割边：在连通图中，删除了连通图的某条边后，图不再连通。这样的边被称为割边，也叫做桥。
割点：在连通图中，删除了连通图的某个点以及与这个点相连的边后，图不再连通。这样的点被称为割点。
DFS搜索树：用DFS对图进行遍历时，按照遍历次序的不同，我们可以得到一棵DFS搜索树。

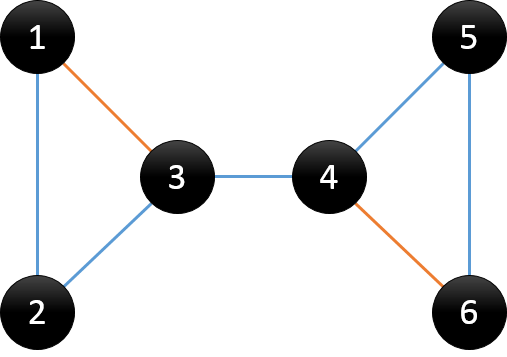
树边：在搜索树中的蓝色线所示，可理解为在DFS过程中访问未访问节点时所经过的边，也称为父子边
回边：在搜索树中的橙色线所示，可理解为在DFS过程中遇到已访问节点时所经过的边，也称为返祖边、后向边
观察DFS搜索树，我们可以发现有两类节点可以成为割点。对根节点u，若其有两棵或两棵以上的子树，则该根结点u为割点；对非叶子节点u(非根节点)，若其中的某棵子树的节点均没有指向u的祖先节点的回边，说明删除u之后，根结点与该棵子树的节点不再连通；则节点u为割点。对于根结点，显然很好处理；但是对于非叶子节点，怎么去判断有没有回边是一个值得深思的问题。我们用dfn[u]记录节点u在DFS过程中被遍历到的次序号，low[u]记录节点u或u的子树通过非父子边追溯到最早的祖先节点(即DFS次序号最小)，那么low[u]的计算过程如下。

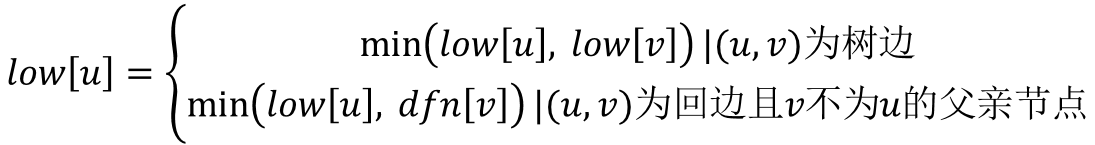
对于给的例子，其求出的dfn和low数组如下。
id     123456
dfn   123456
low   111444
可以发现，对于情况2，当(u,v)为树边且low[v]≥dfn[u]时，节点u才为割点。而当(u,v)为树边且low[v]>dfn[u]时，表示v节点只能通过该边(u,v)与u连通，那么(u,v)即为割边。tarjan算法的时间复杂度是O(n+m)的，非常快。

题意：给出一幅无向图，然后进行加边，每加一条边，询问图中割边的数量

思路：每次加边，把u-v-lca(u,v)-u这个环上的割边减掉。

 

 //2017-08-20
 #include <cstdio>
 #include <cstring>
 #include <iostream>
 #include <algorithm>

 using namespace std;

 const int N = ;
 const int M = ;
 int head[N], tot;
 struct Edge{
     int to, next;
 }edge[M<<];

 void init(){
     tot = ;
     memset(head, -, sizeof(head));
 }

 void add_edge(int u, int v){
     edge[tot].to = v;
     edge[tot].next = head[u];
     head[u] = tot++;

     edge[tot].to = u;
     edge[tot].next = head[v];
     head[v] = tot++;
 }

 int n, m, deep, ans;
 int dfn[N];//dfn[u]记录节点u在DFS过程中被遍历到的次序号
 int low[N]; //low[u]记录节点u或u的子树通过非父子边追溯到最早的祖先节点(即DFS次序号最小)
 int fa[N];//保存dfs树的信息
 int level[N];//记录节点在dfs树中的深度
 int bridge[N];//记录割边，若bridge[u] == 1, 则<u, fa[u]>为一条割边

 void tarjan(int u, int father){
     fa[u] = father;
     dfn[u] = low[u] = deep++;
     level[u] = level[father]+;
     for(int i = head[u]; i != -; i = edge[i].next){
         int v = edge[i].to;
         if(dfn[v] == -){
             tarjan(v, u);
             low[u] = min(low[u], low[v]);
             if(low[v] > dfn[u]){
                 bridge[v] = ;
                 ans++;
             }
         }else if(v != father)
               low[u] = min(low[u], dfn[v]);
     }
 }

 void lca(int a, int b){
     while(level[a] > level[b]){
         if(bridge[a]){
             ans--;
             bridge[a] = ;
         }
         a = fa[a];
     }
     while(level[b] > level[a]){
         if(bridge[b]){
             ans--;
             bridge[b] = ;
         }
         b = fa[b];
     }
     while(a != b){
         if(bridge[a]){
             ans--;
             bridge[a] = ;
         }
         if(bridge[b]){
             ans--;
             bridge[b] = ;
         }
         a = fa[a];
         b = fa[b];
     }
 }

 int main()
 {
     //freopen("inputD.txt", "r", stdin);
     int kase = ;
     while(scanf("%d%d", &n, &m)!=EOF && (n || m)){
         printf("Case %d:\n", ++kase);
         init();
         int u, v;
         for(int i = ; i < m; i++){
             scanf("%d%d", &u, &v);
             add_edge(u, v);
         }
         memset(bridge, , sizeof(bridge));
         memset(dfn, -, sizeof(dfn));
         memset(low, , sizeof(low));
         level[] = ;
         deep = ;
         tarjan(, );
         int q;
         scanf("%d", &q);
         while(q--){
             scanf("%d%d", &u, &v);
             if(ans)lca(u, v);
             printf("%d\n", ans);
         }
         printf("\n");
     }

     return ;
 }