卷积神经网络（CNN）之一维卷积、二维卷积、三维卷积详解

作者：szx_spark
由于计算机视觉的大红大紫，二维卷积的用处范围最广。因此本文首先介绍二维卷积，之后再介绍一维卷积与三维卷积的具体流程，并描述其各自的具体应用。

1. 二维卷积

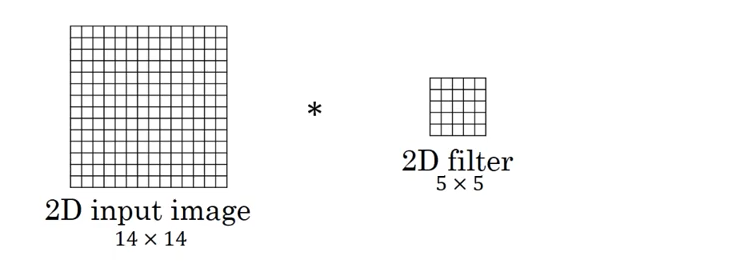
• 图中的输入的数据维度为\(14\times 14\)，过滤器大小为\(5\times 5\)，二者做卷积，输出的数据维度为\(10\times 10\)（\(14-5+1=10\)）。如果你对卷积维度的计算不清楚，可以参考我之前的博客吴恩达深度学习笔记（deeplearning.ai）之卷积神经网络（CNN）（上）。

• 上述内容没有引入channel的概念，也可以说channel的数量为1。如果将二维卷积中输入的channel的数量变为3，即输入的数据维度变为（\(14\times 14\times 3\)）。由于卷积操作中过滤器的channel数量必须与输入数据的channel数量相同，过滤器大小也变为\(5\times 5\times 3\)。在卷积的过程中，过滤器与数据在channel方向分别卷积，之后将卷积后的数值相加，即执行\(10\times 10\)次3个数值相加的操作，最终输出的数据维度为\(10\times 10\)。

• 以上都是在过滤器数量为1的情况下所进行的讨论。如果将过滤器的数量增加至16，即16个大小为\(10\times 10\times 3\)的过滤器，最终输出的数据维度就变为\(10\times 10\times 16\)。可以理解为分别执行每个过滤器的卷积操作，最后将每个卷积的输出在第三个维度（channel 维度）上进行拼接。

• 二维卷积常用于计算机视觉、图像处理领域。

2. 一维卷积

• 图中的输入的数据维度为8，过滤器的维度为5。与二维卷积类似，卷积后输出的数据维度为\(8-5+1=4\)。

• 如果过滤器数量仍为1，输入数据的channel数量变为16，即输入数据维度为\(8\times 16\)。这里channel的概念相当于自然语言处理中的embedding，而该输入数据代表8个单词，其中每个单词的词向量维度大小为16。在这种情况下，过滤器的维度由\(5\)变为\(5\times 16\)，最终输出的数据维度仍为\(4\)。

• 如果过滤器数量为\(n\)，那么输出的数据维度就变为\(4\times n\)。

• 一维卷积常用于序列模型，自然语言处理领域。

3. 三维卷积

这里采用代数的方式对三维卷积进行介绍，具体思想与一维卷积、二维卷积相同。

• 假设输入数据的大小为\(a_1\times a_2\times a_3\)，channel数为\(c\)，过滤器大小为\(f\)，即过滤器维度为\(f\times f\times f\times c\)（一般不写channel的维度），过滤器数量为\(n\)。

• 基于上述情况，三维卷积最终的输出为\((a_1-f+1)\times (a_2-f+1)\times (a_3-f+1)\times n\)。该公式对于一维卷积、二维卷积仍然有效，只有去掉不相干的输入数据维度就行。

• 三维卷积常用于医学领域（CT影响），视频处理领域（检测动作及人物行为）。