基本ILS面的评估
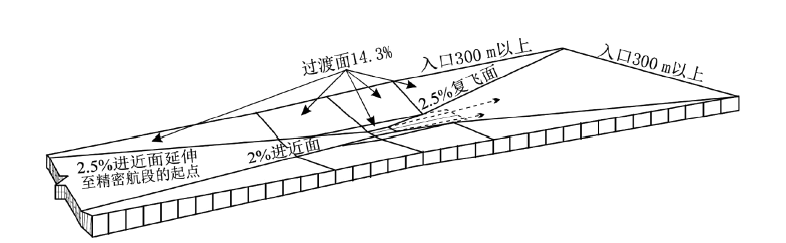
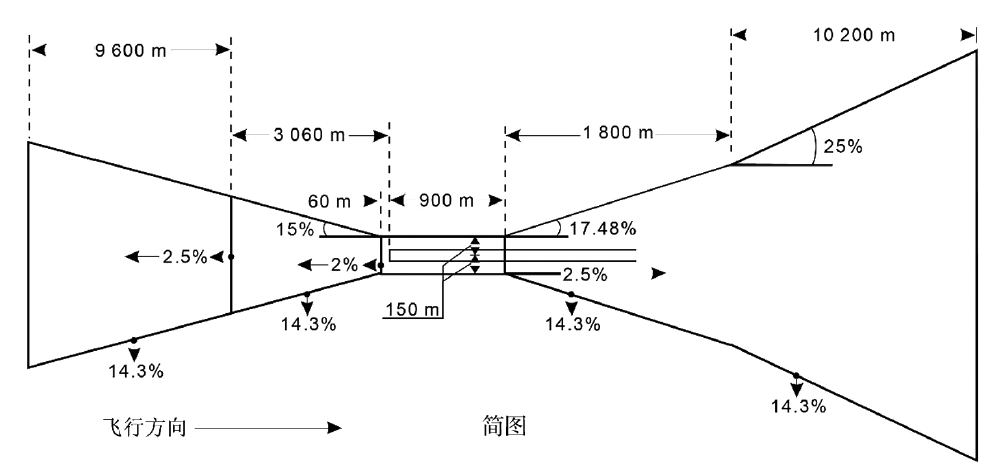
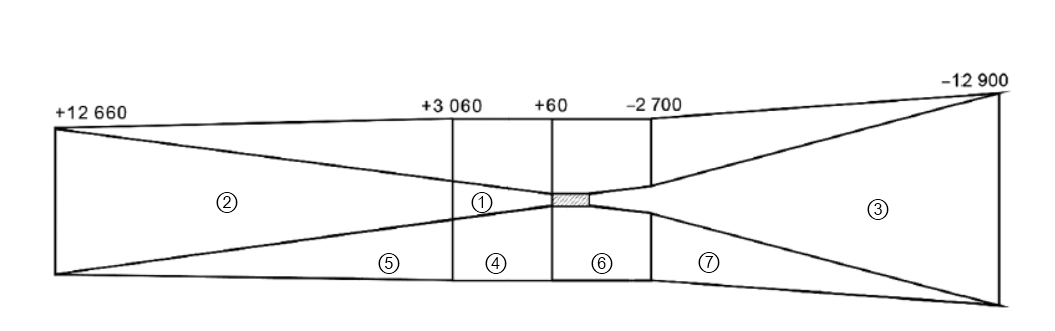
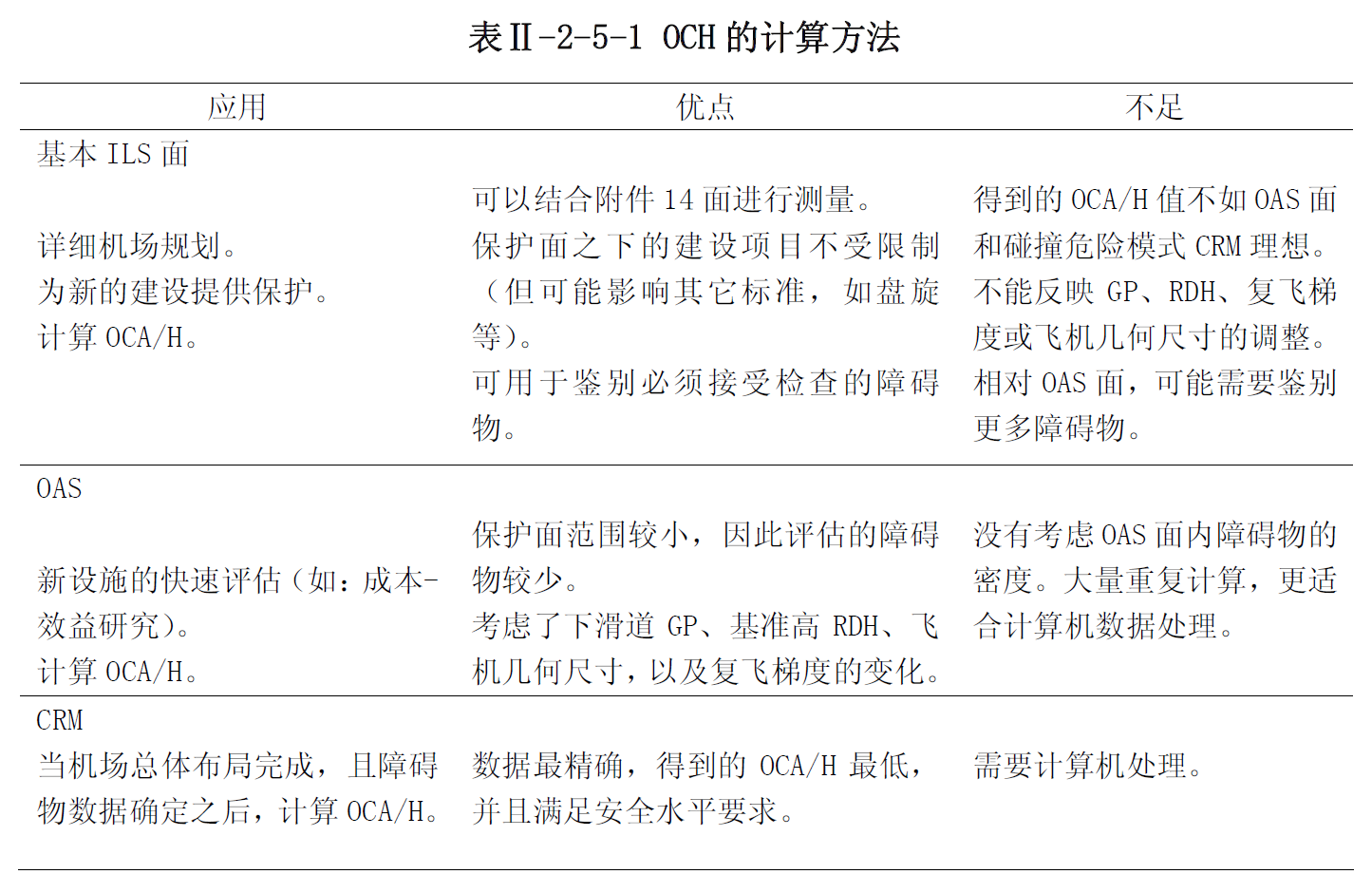
基本ILS面的评估的更多相关文章
- CTO为何要微服务评估
为什么定义参考模型 之前我的工作,大部分时间都是聚焦在某个产品/团队,为他们提供微服务/DevOps的实施及指导.进入公司后,同时参与了多个产品团队的改造研讨.其中最大的不同在于: 在面对一个团队的时 ...
- SQL Server调优系列基础篇(并行运算总结)
前言 上三篇文章我们介绍了查看查询计划的方式,以及一些常用的连接运算符.联合运算符的优化技巧. 本篇我们分析SQL Server的并行运算,作为多核计算机盛行的今天,SQL Server也会适时调整自 ...
- H5版俄罗斯方块(3)---游戏的AI算法
前言: 算是"long long ago"的事了, 某著名互联网公司在我校举行了一次"lengend code"的比赛, 其中有一题就是"智能俄罗斯方 ...
- [转]产品需求文档(PRD)的写作
产品需求对产品研发而言非常重要,写不好需求,后面的一切工作流程与活动都会受到影响.转载一篇文章,关于产品需求文档写作方面的,如下: 本文摘自(一个挺棒的医学方面专家):http://www.cnblo ...
- SQL Server调优系列基础篇 - 并行运算总结(一)
前言 上三篇文章我们介绍了查看查询计划的方式,以及一些常用的连接运算符.联合运算符的优化技巧. 本篇我们分析SQL Server的并行运算,作为多核计算机盛行的今天,SQL Server也会适时调整自 ...
- K-Means 算法(转载)
K-Means 算法 在数据挖掘中, k-Means 算法是一种 cluster analysis 的算法,其主要是来计算数据聚集的算法,主要通过不断地取离种子点最近均值的算法. 问题 K-Means ...
- 第 15 章 可扩展性设计之 Cache 与 Search 的利用
前言: 前面章节部分所分析的可扩展架构方案,基本上都是围绕在数据库自身来进行的,这样是否会使我们在寻求扩展性之路的思维受到“禁锢”,无法更为宽广的发散开来.这一章,我们就将跳出完全依靠数据库自身来改善 ...
- AlphaGo的前世今生(三)AlphaGo Zero: AI Revolution and Beyond
这是本专题的第三节,在这一节我们将以David Silver等人的Natrue论文Mastering the game of Go without human knowledge为基础讲讲AlphaG ...
- kmeans聚类理论篇
前言 kmeans是最简单的聚类算法之一,但是运用十分广泛.最近在工作中也经常遇到这个算法.kmeans一般在数据分析前期使用,选取适当的k,将数据分类后,然后分类研究不同聚类下数据的特点. 本文记录 ...
随机推荐
- k8s之集群管理
导读 经过前面k8s系列的文章,这一系列已经基本完成,现在就用几篇文章说一下日常的集群维护. 目录 更新资源对象的Label Namespace:集群环境共享与隔离 部署集群监控 部署Web UI管理 ...
- FortiGate防火墙办公网常用配置
1.建立主备机 2.配置端口 3.配置SD-WAN 4.新建上网路由 5.新建上网策略 6.建立与其他点的IPSec VPN或点对点专线
- 【疑】接入交换机lacp port-channel连接核心突然中断
现状: 职场网络架构为接入交换机2个端口通过lacp协议的active模式组成port-channel上联到核心. 具体配置如下 接入: 核心: 故障现象: zabbix监控到核心交换机对应该接入交换 ...
- SSH 登录警告:WARNING: REMOTE HOST IDENTIFICATION HAS CHANGED!
1.使用Linux SSH登录其他Linux或者cisco交换机时有如下报错 WARNING: REMOTE HOST IDENTIFICATION HAS CHANGED! (远程主机标识已更改) ...
- Java排序算法(二)选择排序
一.测试类SortTest import java.util.Arrays; public class SortTest { private static final int L = 20; publ ...
- WinformGDI+入门级实例——扫雷游戏(附源码)
写在前面: 本文将作为一个入门级的.结合源码的文章,旨在为刚刚接触GDI+编程或对相关知识感兴趣的读者做一个入门讲解.游戏尚且未完善,但基本功能都有,完整源码在文章结尾的附件中. 整体思路: 扫雷的游 ...
- Spring学习笔记2
一.什么是AOP 面向切面编程,通过预编译方式和运行期动态代理实现程序功能的统一维护的一种技术.在不影响原来功能代码的基础上,使用动态代理加入自己需要的一些功能(比如权限的验证,事务的控制,日志的记录 ...
- 2019牛客暑期多校训练营(第一场)E ABBA (DP/卡特兰数)
传送门 知识点:卡特兰数/动态规划 法一:动态规划 由题意易知字符串的任何一个前缀都满足\(cnt(A) - cnt(B) \le n , cnt(B)-cnt(A)\le m\) \(d[i][j] ...
- Codeforces Round #651 (Div. 2) E. Binary Subsequence Rotation(dp)
题目链接:https://codeforces.com/contest/1370/problem/E 题意 给出两个长为 $n$ 的 $01$ 串 $s$ 和 $t$,每次可以选择 $s$ 的一些下标 ...
- codeblocks从安装到环境配置
在去官网下载codeblocks的时候可不要只下载一个外壳: 这个就是外壳 你安装之后还是不能编译程序<_> 你要下载集成环境,例如 这样这里面已经带了一些编译器,你就不需要去下载各种插件 ...
