STL测试3）优先级队列实现二叉堆

用法：

big_heap.empty();判断堆是否为空

big_heap.pop();弹出栈顶元素最大值

big_heap.push（x）;将x添加到最大堆

big_heap.top();返回栈顶元素;

big_heap.size();返回堆中元素个数

简单的应用

#include<stdio.h>
#include<queue>
#include<vector>
#include<functional>

using namespace std;

int main()
{

priority_queue <int> big_heap;//默认构造是最大堆
priority_queue<int, vector<int>, greater<int> > small_heap;//最小堆
priority_queue<int, vector<int>, less<int> > big_heap2;//最大堆
if(big_heap.empty())
{
    printf("big_heap is empty\n");
}
int test[]={,,,,,,};

for(int i=;i< ;i++)
{

    big_heap.push(test[i]);
    small_heap.push(test[i]);
    printf("input %d,big_heap top is %d ,small_heap top is%d\n",test[i],big_heap.top(),small_heap.top());
}
big_heap.push();
small_heap.push();
printf("now big_heap top is %d\nnow small_heap top is %d\n",big_heap.top(),small_heap.top());

for(int i=;i<;i++)
{

    big_heap.pop();
    small_heap.pop();
}

printf("now heap has %d num,the max is %d,the min is%d\n",big_heap.size(),big_heap.top(),small_heap.top());
return ;
}

下面来一个简单的应用

在未排序的数组中找到第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

示例 1:

输入: [3,2,1,5,6,4] 和 k = 2
输出: 5
示例 2:

输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4
说明:

你可以假设 k 总是有效的，且 1 ≤ k ≤ 数组的长度。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/kth-largest-element-in-an-array
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路：

维护一个K大小的最小堆，如果堆中栈顶的元素＜k，直接入堆；此外情况如果堆顶的元素小于新元素的时候，弹出堆顶，将新元素入堆。

这样保证堆外的元素都是比堆顶小的，不然会把该元素和堆顶的元素置换，这样保证最后堆里存的是k个最大的元素，且堆顶是这k个元素里最小的。那么堆顶倒数第k小的就是第k大的了。

代码写在下面。

class Solution {

public:

    int findKthLargest(vector<int>& nums, int k) {

    priority_queue<int, vector<int>, greater<int> > small_heap;

    for(int i=0;i<nums.size();i++)

    {

        if(i<k)

        {

            

             small_heap.push(nums[i]);

        }

        else if( small_heap.top()<nums[i])

        {

            small_heap.pop();

             small_heap.push(nums[i]);

        }

    }

    return  small_heap.top();

    }

};

下面是一个利用最大堆和最小堆求中位数的问题。

中位数是有序列表中间的数。如果列表长度是偶数，中位数则是中间两个数的平均值。

例如，

[2,3,4] 的中位数是 3

[2,3] 的中位数是 (2 + 3) / 2 = 2.5

设计一个支持以下两种操作的数据结构：

void addNum(int num) - 从数据流中添加一个整数到数据结构中。
double findMedian() - 返回目前所有元素的中位数。
示例：

addNum(1)
addNum(2)
findMedian() -> 1.5
addNum(3)
findMedian() -> 2
进阶:

如果数据流中所有整数都在 0 到 100 范围内，你将如何优化你的算法？
如果数据流中 99% 的整数都在 0 到 100 范围内，你将如何优化你的算法？

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/find-median-from-data-stream
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路就是设计一个最大堆和最小堆分别存储一般数据，并维持两个堆中最大堆的堆顶比最小堆小。这样如果两个堆大小相同，那么中位数就是两个堆顶的平均值，如果是堆大小不同，那么中位数就是size大的那个堆的堆顶。

看到一个别人画的示意图，非常形象，这里搬过来方便以后理解。

addNum 函数设计

  addNum() 函数在添加元素的过程中保持两个堆的动态平衡：

Condition 1.保证两堆元素个数相差不超过 1
Condition 2.保证大顶堆中的元素小于等于小顶堆中的任何元素

case 1:

• 如果两堆中的元素个数相同。这个时候无论插入哪一个堆，条件 1 都不会被破坏,因此考虑条件 2 ，将待插入元素与两堆的堆顶比较:若待插入元素为 5，显然这个时候若插入smaller会破坏条件 2，因此因插入bigger中。而若待插入为 9 则显然应插入 smaller 中。

---

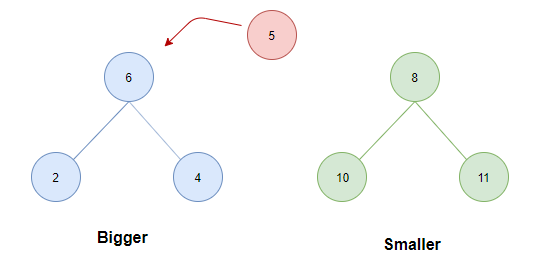
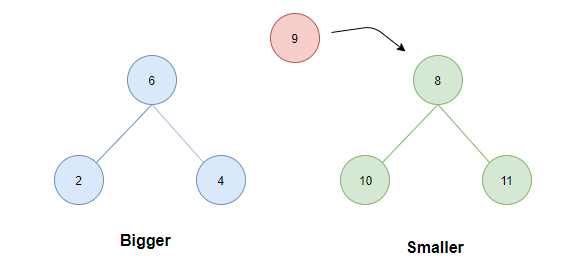
case 2:

• 如果大顶堆元素个数小于小顶堆的元素个数。此时，将待插入元素与两堆堆顶比较:
• 若小于等于Bigger.top则直接插入Bigger中；

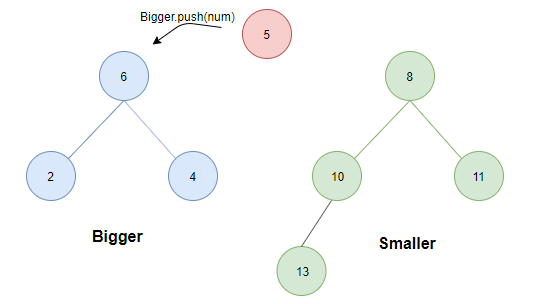
• 若大于smaller.top则为了保证条件1,需将smaller中的最小值（根）转存至Bigger中。

---

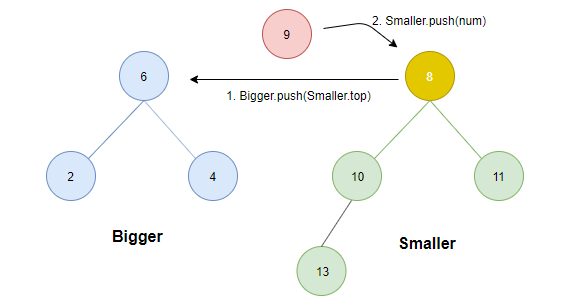
case 3:

• 如果大顶堆的元素个数大于小顶堆的元素个数。此时，将待插入元素与两堆堆顶比较：
• 若其大于等于Smaller.top则直接插入Smaller中；

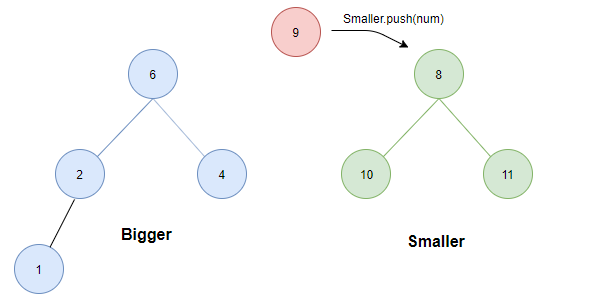
• 若小于Bigger.top则为了保证条件1，需将Bigger中的最大元素值（根）转存至Smaller中。

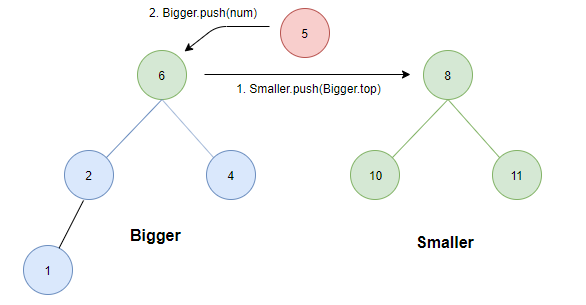
最后是实现以后的代码：

class MedianFinder {
public:
    priority_queue <int> big_queue;
    priority_queue<int, vector <int>, greater <int> > small_queue;
    /** initialize your data structure here. */
    MedianFinder() {

    }

    void addNum(int num) {
        if(big_queue.empty())
        {
            big_queue.push(num);
            return;
        }
        if(big_queue.size() == small_queue.size())
        {
            if(num < big_queue.top())
            {
                big_queue.push(num);
            }
            else
            {
                small_queue.push(num);
            }
        }
        else if(big_queue.size() > small_queue.size())
        {
            if(num > big_queue.top())
            {
                small_queue.push(num);
            }
            else
            {
                small_queue.push(big_queue.top());
                big_queue.pop();
                big_queue.push(num);
            }
        }
        else if(big_queue.size() < small_queue.size())
        {

            if(num < small_queue.top())
            {
                big_queue.push(num);
            }
            else
            {
                big_queue.push(small_queue.top());
                small_queue.pop();
                small_queue.push(num);
            }
        }

    }

    double findMedian() {
        if(big_queue.size() == small_queue.size())
            return ((big_queue.top()+small_queue.top())/2.0);
        else if(big_queue.size() > small_queue.size())
            return big_queue.top();
        else
            return small_queue.top();

    }
};