蕴含式（包含EXISTS语句的分析）

*{
font-family: STFangSong;
outline: none;
}

蕴含式

一、蕴含式基础

（Ⅰ）什么是“蕴含式”

设p、q为两个命题。复合命题“如果p，则q”称为p与q的蕴含式，记作p→q，并称p为蕴含式的前件，q为后件。定义中规定p→q为假当且仅当p为真q为假。

或许有同学会问：我发现这个“蕴含式”好像我们高中时所学的“命题”。自信一点，把“好像”去掉，只不过“蕴含式”比高中时所学的“命题”的范围更广一些。

（Ⅱ）“蕴含式”的意义

不难发现，“蕴含式”的逻辑关系为：q是p的必要条件，p是q的充分条件。也就是说诸如“只要p就q”、“q仅当p”、“只有p才q”...等，都可以符号化为p→q的形式。

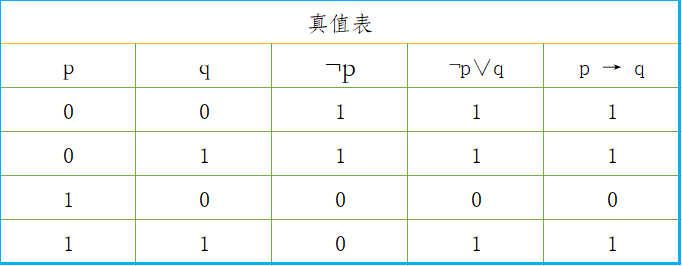
（Ⅲ）“蕴含式”的真值表( True Table )

二、理解的误区

在我们平时遇到的“p→q”要么是p与q之间存在着一定的联系，要么是在前件p为真的前提下作出的判断。就比如我们在高中时学过的“命题”，它的形式是“若p，则q”，形式与“蕴含式”一模一样，但是细心的同学就会发现，我们在研究问题的时候通常将前件p视为真命题，然后再来研究后件q的真假性，从而判断“命题”真假性。所以说我们用以前高中的的思路是很难理解这个真值表（True Table）的。

　　

但是要是真想理解起来倒也不是很难，举个栗子：这里存在着一个蕴含式“如果我当上了班长，我将提高同学的福利”。所以不妨设，前件p为“我当上了班长”，后件q为“我将提高同学的福利”，那么这个蕴含式就可以符号化为p→q，记为I。

所以问题就是判断I的真假，也就是说我有没有撒谎。

很显然当p为真，q为假的时候，我并没有履行我的诺言，故此时I为"False"。当p为假的时候，不管我有没有提高同学们的福利，你都不能说我没有履行我的诺言，因为我就没有当上班长，此时的I为真。

三、蕴含式中的等价式

【注释】：如果不理解，可以先康康（四），里面有解释为什需要学习等价式

（Ⅰ）量词转换律

①、“存在量词∃”转换为“全称量词∀”：¬【∀x p(x)】 ⇔ 【∃x¬p(x)】；

②、“全称量词∀”转换为“存在量词∃”：¬【∃x q(x)】 ⇔ 【∀x¬q(x)】；

（Ⅱ）含量词的合取式、析取式的等价式

①、“全称量词∀”只对合取式的分配：∀x（p(x) Λ q(x)） ⇔【∀x p(x)】Λ【∀x q(x)】；

②、“存在量词∃”只对析取式的分配：∃x（p(x)∨q(x)） ⇔ 【∃x p(x)】∨【∃x q(x)】；

（Ⅲ）量词辖域的扩张和收缩(八个等价式)

（1）若量词的辖域中是合取式(Λ)或者析取式(∨)，那么对于不受约束的谓词公式(q)可以直接进入或者退出该辖域

①、∀x（p(x) Λ q） ⇔ 【∀x p(x)】Λ q，同样的对于∀x（p(x)∨q） ⇔ 【∀x p(x)】∨ q也成立；

②、∃x（p(x)∨q） ⇔ 【∃x p(x)】∨ q， 同样的对于∃x（p(x)Λq） ⇔ 【∃x p(x)】Λ q也成立；

（2）若量词的辖域中是“蕴含式”的前件，那么作为后件的不受约束的谓词公式不可以直接进入或者退出该辖域

①、【∀x p(x)】→ q ⇔ ¬【∀x p(x)】∨q ⇔ 【∃x¬p(x)】∨q ⇔ ∃x（¬p(x)∨q） ⇔ ∃x（p(x) → q）；

②、【∃x p(x)】→ q ⇔ ¬【∃x p(x)】∨q ⇔ 【∀x¬p(x)】∨q ⇔ ∀x（¬p(x)∨q） ⇔ ∀x（p(x) → q）；

（3）若量词的辖域是“蕴含式”的后件，则作为前件的不受约束的谓词公式可以直接进入或者退出该辖域

①、q → 【∀x p(x)】 ⇔ ¬q ∨【∀x p(x)】 ⇔ ∀x（¬q∨p(x)） ⇔ ∀x（q → p(x)）；

②、q → 【∃x p(x)】 ⇔ ¬q ∨【∃x p(x)】 ⇔ ∃x（¬q∨p(x)） ⇔ ∃x（q → p(x)）；

（Ⅳ）“蕴含式” && 德摩根律

（1）普通(我愿称之为常量)“蕴含式” && 德摩根律 的等价式

①、“蕴含式”的等价式：p→q ⇔ ¬p∨q ；

②、德摩根律：¬（p∨q） ⇔ ¬pΛ¬q ；

（2）自由元组变量在 “蕴含式” && 德摩根律 的等价式

①、“蕴含式”的等价式：p(x)→q(x) ⇔ ¬p(x)∨q(x)；

②、德摩根律：¬（p(x)∨q(x)） ⇔ ¬p(x) Λ ¬q(x)；

（3）约束元组变量在 “蕴含式” && 德摩根律 的等价式

①、“蕴含式”的等价式：【∀x p(x)】→【∃x q(x)】 ⇔ ¬【∀x p(x)】∨【∃x q(x)】 ⇔ 【∃x¬p(x)】∨【∃x q(x)】 ⇔ ；

②、德摩根律：¬（【∀x p(x)】∨【∃x q(x)】） ⇔ ¬【∀x p(x)】Λ¬【∃x q(x)】；

（Ⅴ）在SQL中我们重点掌握这样几个点：

【注释】：在下面（四）中会解释为什么要这样

（1）基础部分（主要掌握其形式）：

①、蕴含式的等价式（其形式与x以及辖域无关）：p→q ⇔ ¬p∨q；

②、德摩根律（长横变短横，开口换方向）：¬（p∨q） ⇔ ¬p Λ ¬q；

③、量词转换律（量词互换，命题加非），比如：¬【∀x p(x)】 ⇔ 【∃x¬p(x)】；

（2）提高部分（SQL中的条件很少有常量条件）：

①、含量词的合取式、析取式的等价式（存在析取，全称合取）；

②、量词辖域的扩张和收缩（1）；

③、量词辖域的扩张和收缩（2）（3）—— 可以根据前面的公式自己推；

（3）困难部分（常用）：

①、集合X是集合Y的父级（对于任意的x属于X，总是存在一个y属于Y，使得“x=y”成立）：

\(\forall\ x【x(X)\ \rightarrow\ \exists\ y【y(Y)\ \bigwedge\ x=y】】\) ⇔ \(\forall\ x【\ ^¬x(X)\ \bigvee\ \exists\ y【y(Y)\ \bigwedge\ x=y】】\) ⇔

\(\ ^¬【\ ^¬【\forall\ x【\ ^¬x(X)\ \bigvee\ \exists\ y【y(Y)\ \bigwedge\ x=y】】】】\) ⇔ \(\ ^¬【\exists\ x\ ^¬【\ ^¬x(X)\ \bigvee\ \exists\ y【y(Y)\ \bigwedge\ x=y】】】\) ⇔

\(\ ^¬【\exists\ x【x(X)\ \bigwedge\ \ ^¬【\exists\ y【y(Y)\ \bigwedge\ x=y】】】】\)。

更一般的情况，对于任意的x属于X使得p(x)成立，总是存在一个y属于Y，使得“q(x, y)”成立：

\(\forall\ x【p(x)\ \rightarrow\ \exists\ y\ q(x,y)】\) ⇔ \(\ ^¬【\exists\ x【p(x)\ \bigwedge\ \ ^¬【\exists\ y\ q(x,y)】】】\)。

②、集合X和集合Y有交集，严格来说就一种情况，但是为了研究“至少这个关键字”，我们 将此处分为两种情况：

（ⅰ）集合X和集合Y至少有一个公共元素（某个x属于X，总是存在一个y属于Y，使得“x=y”成立）：

\(\exists\ x【x(X)\ \bigwedge\ \exists\ y【y(Y)\ \bigwedge\ x=y】】\)。

更一般的情况，对于某个x属于X满足p(x)，总是存在一个y属于Y满足q(x,y)：

\(\exists\ x【p(x)\ \bigwedge\ \exists\ y\ q(x,y)】\)。

（ⅱ）集合X和集合Y不完全相同（存在某个x属于X，对于任意的y只要属于Y就必然有“x≠y”）：

首先将命题更改一下，也就是将“≠”改成“不＝”，故而有：

\(\exists\ x【x(X)\ \bigwedge\ \forall\ y【y(Y)\ \rightarrow\ \ ^¬（x=y）】】\) ⇔ \(\exists\ x【x(X)\ \bigwedge\ \ ^¬【\exists\ \ y【y(Y)\ \bigwedge\ （x=y）】】】\)。

更一般的情况，存在一个x属于X满足p(x)，对于任意的y只要属于Y就必然有¬q(x,y)：\(\exists\ x【x(X)\ \bigwedge\ \forall\ y【y(Y)\ \rightarrow\ \ ^¬q(x,y)】】\) ⇔ \(\exists\ x【p(x)\ \bigwedge\ \ ^¬【\exists\ \ y\ q(x,y)】】\)。

③、集合X和集合Y莫得交集（对于任意的x只要属于X，必然有对于任意的y只要属于Y，一定满足条件“x≠y”）：

\(\forall\ x【x(X)\ \rightarrow\ \forall\ y【y(Y) \rightarrow\ \ ^¬（x=y）】】\) ⇔ \(\forall\ x【x(X)\ \rightarrow\ \ ^¬【\exists\ y【y(Y) \bigwedge\ x=y】】】\) ⇔

\(\ ^¬【\exists\ x【x(X)\ \bigwedge\ \exists\ y【y(Y) \bigwedge\ x=y】】】\)。

更一般的情况，对于任意的x只要属于X满足p(x)，必然有对于任意的y只要属于Y一定满足条件¬q(x,y)，换一种说法就是，“对于任意的x只要属于X满足p(x)，必然不存在y满足条件q(x,y)”：

\(\forall\ x【p(x)\ \rightarrow\ \ ^¬【\exists\ y\ q(x,y)】】\) ⇔ \(\ ^¬【\exists\ x【p(x)\ \bigwedge\ \exists\ y\ q(x,y)】】\)。

（4）需要注意的地方：

①、必须保证“属于”关系，比如\(x(X)\)必须满足（原因在于最后的SQL语句……）；

②、一般情况下“\(\forall\)”后面都会加上“蕴含式\(\rightarrow\)”，“\(\exists\)”后面则很少会有蕴含式。

其实通过解读蕴含式的含义：“只要p就有q”，不难发现在运用全称量词的时候，我们会运用句式“对于任意的x满足p(x)都有q(x)成立”，这句话有一种“自然而然就绑定了”的意思：“只要x满足p(x)那么就会有q(x)”。

反观存在量词，我们用的最多的就是“总是存在一个x满足p(x)，使得q(x)成立”，这个“使得”二字就没有了“自然而然”的韵味了，就是一种特殊的情况，不能说x满足p(x)后就一定有q(x)，只能是某一个x满足p(x)后恰好也能满足q(x)。

不过也有一种情况时存在量词后面加上蕴含式，比如范数的某个定理（《数值分析》\(P_{163}\ 定理15\)）“如果在一种范数意义下向量序列收敛时，则在任何一种范数意义下该向量序列均收敛”，即“存在一个x满足p(x)，必然有对于任意的x都有q(x)”，这里的q(x)和p(x)是等价的—属于X并且向量序列收敛：

\(\exists\ x【p(x)\ \rightarrow\ \forall\ x\ q(x)】\)。当然这个式子不能表达出推论“存在一个x不满足p(x)，必然有对于任意的x都不满足q(x)”，因为我们没有办法控制命题变换为“\(x(X)\ \bigwedge\ \ ^¬m(x)\)”，其中\(m(x)\)就是向量序列收敛。

③、在（3）.②中，求相交的时候并不是严格意义上的相交，因为在（ⅰ）中包含了（3）.①的情况，在（ⅱ）中包含了（3）.③的情况。但是这并没有影响到我们使用，因为我们一般遇到的相交的问题都是“至少”问题，不会说让我们求“集合X和Y有共同的非空元素，并且两集合不互相包含”，这样很恶心，而解决“至少”的问题一般会用其否命题“全部”问题求非来解决，所以我们就不用考虑严格意义上的相交了。

但是话又说回来，如果真的遇上了就在（3）.②.（ⅰ）和（3）.②.（ⅱ）之间加上合取式：

\(\exists\ x【p(x)\ \bigwedge\ \exists\ y\ q(x,y)】\quad\bigwedge\quad\exists\ x【p(x)\ \bigwedge\ \ ^¬【\exists\ \ y\ q(x,y)】】\)。但是千万注意存在量词只能对析取式进行分配。

④、【注意：】

（ⅰ）“全称量词∀”可以对合取式进行分配，但是不能对析取式进行分配。

这句话从另一角度上来说：\(【\forall\ x\ p(x)】\) ⇔ \(p(a_1)\bigwedge…\bigwedge p(a_n)\)；

（ⅱ）“存在量词∃”可以对析取式进行分配，但是不能对合取式进行分配。

这句话从另一角度上来说：\(【\exists\ x\ p(x)】\) ⇔ \(p(a_1)\bigvee…\bigvee p(a_n)\)；

四、所以说……我到底想要表达什么？

​ 当某一个命题为条件命题(也就是“蕴含式”)的时候，记为p→q。这所表达的意思就是：当p为真并且p→q也为真的情况下(这一前提常常被人们忽略，认为这是理所当然的)，发生了p事件就一定能发生q事件。我们将p和q视为两个集合，不难理解，这时就能得到p⊆q。

​ 所以表示两个集合是父子集合的时候，可以这样来表述：\(\forall\ x【p(x)\in P \rightarrow \exists\ y【q(y)\in Q\ \bigwedge\ p(x)=q(y)】】\)。

我们可以这样来分析一下：

①、\(\forall\ x【Condition】\) —— 对于任意的x都要满足某个条件，这个条件用Condition来代指；

②、\(Condition\)：\(p(x)\in P \rightarrow \exists\ y【q(y)\in Q\ \bigwedge\ p(x)=q(y)】\) —— 这个条件是：只要p(x)属于P集合中，那么总能找到某一个y,使得q(y)属于Q集合,并且有p(x)=q(y)成立；

​ 很好理解吧，但是这里我并不只是bb离散数学，而是要将这玩意儿和SQL的实际情况相结合。在SQL中有一个很巧妙但是让人们感到十分蛋疼的一个机制：没有“全称量词∀”。这时我们就需要运用上面所学到的相关知识，将这些“全称量词∀”转换为“存在量词∃”。怎样表述命题之间的关系、怎样转换为不含“全称量词∀”的命题，这些在（三）中已经有所了解了，那我们来看下面一个实例。

诉求：查询选修了全部课程的学生的姓名和学号。

元组关系运算的表达式：

\(\{new\_s^{(2)}\) |

　　\(\exists\ s\)【 # 总是存在一个s满足条件：

　　　　\(s(S)\ \bigwedge\) # s∈S

　　　　\(\forall\ c【c(C) \rightarrow\) # 对于任意的c满足条件：只要c∈C，那么一定有存在某个sc满足条件：

　　　　　　\(\exists\ sc【sc(SC)\ \bigwedge\ sc.sno = s.sno\ \bigwedge\ sc.cno = c.cno】\) # sc∈SC，并且使得sc.sno = s.sno和sc.cno = c.cno同时成立 —— 意思就是C.CNo集合是SC.CNo集合的子集，并且将这个集合连接起来；

　　　　】

　　】 Λ

　　\(new\_s[1] = s[1]\ \bigwedge\)

　　\(new\_s[2] = s[2]\)

\(\}\)。

​ 但是终究不能用元组关系演算来进行筛选，还得转换为SQL标准语言。用到（三）中的公式：

（1）首先将元组关系演算分解、简化：∃s, s(S) Λ p，即为存在s满足条件：s∈S，并且p；

【注释】：其中的p为“\(\forall\ c【c(C)\ \rightarrow\ \exists\ sc【sc(SC)\ \bigwedge\ sc.sno = s.sno\ \bigwedge\ sc.cno = c.cno】】\)”。

（2）其次将归属关系p(P)尽量去掉，进一步简化，因为归属关系在SQL统一用“SELECT 字段名 FROM 表”来表述；

【注释】：其中p为“\(\forall\ c【c(C)\ \rightarrow\ \exists\ sc【sc.sno = s.sno\ \bigwedge\ sc.cno = c.cno】】\)”。

（3）灵活运用“蕴含式”公式，将能合并的合并，使得最后的形式为：

\(\exists\ p_1【Conditions\ \bigwedge\ \exists\ p_2【Conditions\ \bigwedge\ 【...\exists\ p_n【Conditions】】】】\)。那么根据这一点将p化简就有：

\[\begin{aligned}
p &= \forall\ c【\ ^¬c(C)\ \or\ \exist\ sc【sc.sno = s.sno\ \and\ sc.cno = c.cno】】\\
&= \forall\ c【\exist\ sc【sc.sno = s.sno\ \and\ sc.cno = c.cno】】\\
&= \ ^¬【\exist\ c\ \ ^¬【∃sc【sc.sno = s.sno\ \and\ sc.cno = c.cno】】】\\
\end{aligned}
\]

（4）所以最后的形式为：\(\exists\ s\ \ ^¬【\exists\ c\ \ ^¬【∃sc【sc.sno = s.sno\ \bigwedge\ sc.cno = c.cno】】】\)。

​ 转换为SQL语句：

SELECT SNo, SN
FROM S
WHERE
	NOT EXISTS (
		SELECT *
		FROM C
		WHERE
			NOT EXISTS (
				SELECT *
				FROM SC
				WHERE CNo = C.CNo AND SNo = S.SNo
			)
    )

​ 这里其实有一个很容易弄错的地方：误以为连接SC表和S表的元组变量要单独写一个“\(\exists\ sc【sc(SC)\ \bigwedge\ sc.sno = s.sno】\)”，也就是说将两个表间的连接独立开，各连各的。这个想法非常的幼稚，为什么这样说呢，打一个形象的比方：S表相当于左边的一个岸，C表相当于右边的一个岸，SC表显然就是连接两岸的桥，如果说想要用SC表将C表和S表连起来，那么肯定就需要找到同一个SC表中的元组sc，让它左手牵S表的元组s，同时右手牵着C表的元组c；如果这不是同时牵的话，就很可能导致桥不是同一个桥，即不是同一个sc元组。下面我们是可以通过简单的逻辑证明来表述的。如果我们将这两个连接独立，则会得到：

①、\(p = \exists\ sc【sc.sno = s.sno】\)；

②、按照上述4个步骤简化q表达式

\[\begin{aligned}
q =\qquad &\forall\ c【\ ^¬c(C)\ \or\ \exist\ sc【sc.cno = c.cno】】\\
\overset{去归属关系}{\Longrightarrow} &\forall\ c【\exist\ sc【sc.cno = c.cno】】\\
\overset{转变全称量词}{\Longrightarrow} &\ ^¬【\exist\ c \ ^¬【\exist\ sc【sc.cno = c.cno】】】
\end{aligned}
\]

③、现在的形式为：∃s【p Λ q】,但是并不是“存在量词∃”的迭代形式，还需要进一步合并；

④、由德摩根律得：p Λ q = ¬(¬p ∨ ¬q) = ¬(p → ¬q)；

⑤、将p、q代入得：\(\ ^¬【\exists\ sc\ sc.sno = s.sno\ \rightarrow\ \exists\ c\ \ ^¬【\exists\ sc\ sc.cno = c.cno】】\)；

⑥、由“量词辖域的扩张和收缩”的第三点，前件不受∃c的辖域，所以可以等价为：

\(\ ^¬【\exists\ c\ 【【\exists\ sc\ sc.sno = s.sno】\ \rightarrow\ \ ^¬【\exists\ sc\ sc.cno = c.cno】】】\) ⇔

\(\ ^¬【\exists\ c\ 【\ ^¬【∃sc\ sc.sno = s.sno】\ \bigvee\ \ ^¬【∃sc\ sc.cno = c.cno】】】\)) ⇔

\(\ ^¬【\exists\ c\ \ ^¬【【∃sc\ sc.sno = s.sno】\ \bigwedge\ 【∃sc\ sc.cno = c.cno】】】\)

⑦、很多同学就会将这个等价与“\(\ ^¬【\exists\ c\ \ ^¬【∃sc【sc.sno = s.sno\ \bigwedge\ sc.cno = c.cno】】】\)”结果好像是一模一样，但是这里其实是有一个很大的逻辑错误：由“含量词的合取式、析取式的等价式”的注意事项，我们知道“存在量词∃”只能对析取式进行分配、不能对合取式进行分配。这是因为

“\(【\exists\ x\ p(x)】\ \bigwedge\ 【\exists\ x\ q(x)】\)”和“\(\exists\ x【p(x)\ \bigwedge\ q(x)】\)”之间的关系是“蕴含式”。

我们可以简单的来证明一下：

（1）从左到右：假设前件“\(\exists\ x【p(x)\ \bigwedge\ q(x)】\)”为真，那么存在一个x=c，使得p(c)Λq(c)为真，即存在一个x=c使得p(c)为真，存在一个x=c使得q(c)也为真；故而后件“\(【\exists\ x\ p(x)】\ \bigwedge\ 【\exists\ x\ q(x)】\)”为真；

（2）从右到左：假设后件“\(【\exists\ x\ p(x)】\ \bigwedge\ 【\exists\ x\ q(x)】\)”为真，那么我们只能得到，存在一个x=c使得p(c)为真，存在一个x=b使得q(b)为真，并不能保证b=c，所以由后件得不到前件；

五、总结

（Ⅰ）掌握“蕴含式”，以及什么时候运用；

提示：等价式、德摩根律、收缩与扩张，当表示一个集合是另一个集合的子集时运用“蕴含式”。

（Ⅱ）充分理解“含量词的合取式、析取式的等价式”，从而得出结论：不能将连接操作分开写，必须写在一起，这里的一起是指：保证连接时的元组是同一个。具体表现为：写在靠后的\(WHERE\)语句中，因为要包含较多的\(SELECT\)语句(本质上是表)，使得选择元组是同一个；

提示：“全称量词∀”只可以对合取式进行分配；“存在量词∃”只可以对析取式进行分配。

六、实例

（1）案例_01_以全部课程为准，学生的4种选课情况；

（2）案例_02_以'李力'老师教授的课程为准，学生的5种选课情况；

（3）案例_03_以'数据库'和'JAVA'_教师姓名、编号为准，老师授课的4种选课情况；

（4）案例_04_以全部学生为准，课程被选的4种选课情况(只列举出2种)；

（5）案例_05_关于：至少、至多、恰好；