[Luogu P3469] [POI2008]BLO-Blockade (割点)

题面

传送门：https://www.luogu.org/problemnew/show/P3469

---

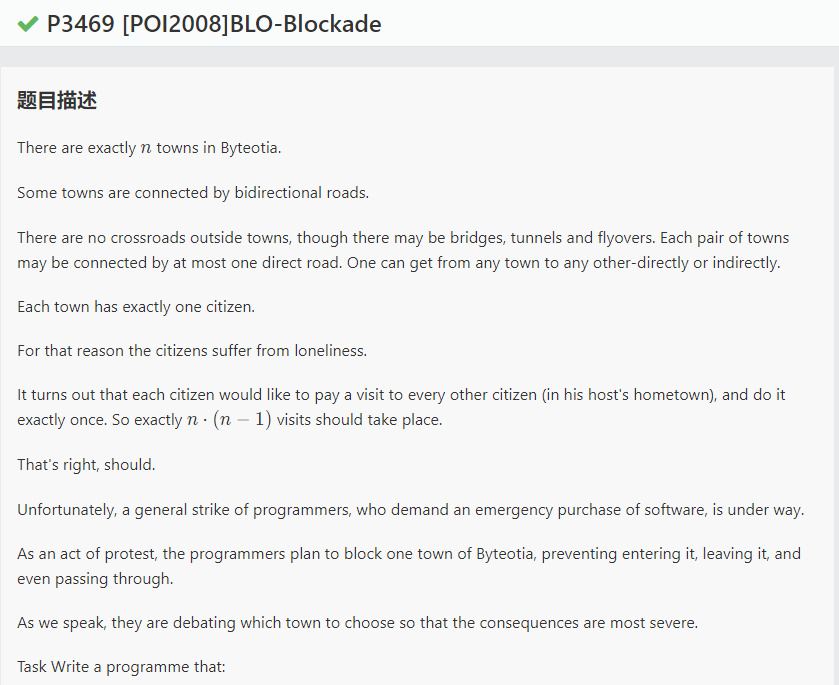
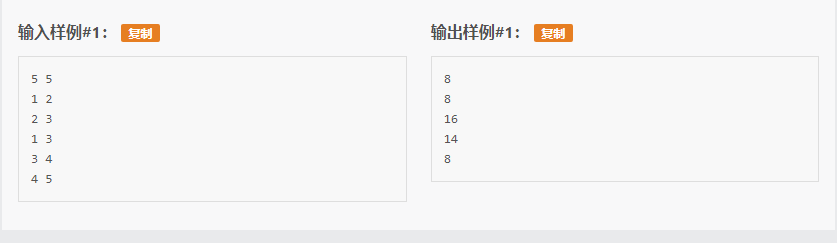
Solution

先跟我大声念：

poi！

然后开始干正事。

首先，我们先把题目中的点分为两类：去除这个点能把图分为几个部分的，去除这个点不影响整个图的连通性的。

如下图：

点上的数字表示这个点的搜索序。

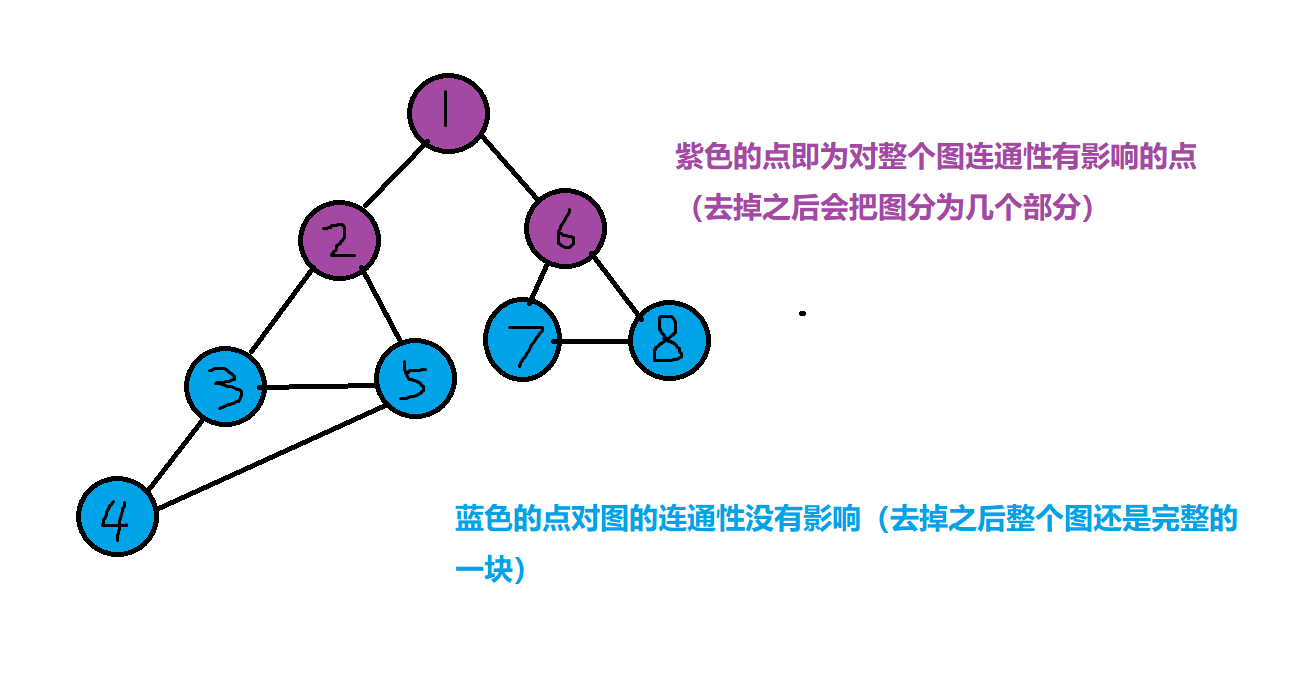
我们称这些对连通性有影响的点为割点。

先假设我们能求出这些点以及其出去后把图分为几块之后那几块分别的大小。

是不是发现了什么？

对于非割点，答案显然是2*(n-1) (因为它不能影响别的点对连通性，能影响的只是别人到它以及它到别人)

对于割点，它把那几块弄得无法联通，即那几块中不同块的两个点肯定就无法联通了，答案也就是每组块的点的数量互相乘出来，再加上2*(n-1)。

接下来就是如何求割点了。

这时候我们又得请出伟大的Tarjan了。

先回忆一下求强连通分块的做法，我们这里求割点的做法与其类似。

但有以下几点不同：

1.我们在求low的时候不用讨论所连向的点是否在栈中了，因为无向图中没有横插边的说法（但是要记录当前的父亲，防止我们的low直接计算回去）

2.当一个点的某一个孩子的low>=此点的dfn时，说明这个点就是割点。因为孩子的low大于当前节点的dfn，说明它没有办法直接从当前节点回到搜索树搜过的节点。如果当前节点删除了，此孩子将会分割开来）

至于怎么求每个孩子的size........

（我想这个应该不用说了吧）

就是搜的时候加上去就好，如果不清楚的话看一下代码就懂了。

时间复杂度O(n)

完全OjbK

---

Code

//Luogu P3469 [POI2008]BLO-Blockade
//June,11th,2018
//玄幻割点
#include<iostream>
#include<cstdio>
#include<vector>
using namespace std;
long long read()
{
    long long x=0,f=1; char c=getchar();
    while(!isdigit(c)){if(c=='-') f=-1;c=getchar();}
    while(isdigit(c)){x=x*10+c-'0';c=getchar();}
    return x*f;
}
const int N=100000+100;
vector <long long> e[N],nd_size[N];
int n,m;
int dfn[N],low[N],IsGD[N],nd_to,size[N];
void Tarjan(int now,int fa)
{
    dfn[now]=low[now]=++nd_to;
    size[now]++;
    int temp=0;
    for(int i=0;i<int(e[now].size());i++)
        if(dfn[e[now][i]]==0)
        {
            Tarjan(e[now][i],now);
            size[now]+=size[e[now][i]];
            low[now]=min(low[now],low[e[now][i]]);
            if(low[e[now][i]]>=dfn[now])
            {
                temp+=size[e[now][i]];
                IsGD[now]=true;
                nd_size[now].push_back(size[e[now][i]]);
            }
        }
        else if(e[now][i]!=fa)
            low[now]=min(low[now],low[e[now][i]]);
    if(IsGD[now]==true and n-temp-1!=0)
        nd_size[now].push_back(n-temp-1);
}
int main()
{
    n=read(),m=read();
    for(int i=1;i<=n;i++)
    {
        e[i].reserve(4);
        nd_size[i].reserve(4);
    }
    for(int i=1;i<=m;i++)
    {
        int s=read(),t=read();
        e[s].push_back(t);
        e[t].push_back(s);
    }

    Tarjan(1,0);

    for(int i=1;i<=n;i++)
    {
        long long ans=2*(n-1);
        if(nd_size[i].size()!=0 and nd_size[i].size()!=1)
        {
            for(int j=0;j<int(nd_size[i].size());j++)
                for(int k=j+1;k<int(nd_size[i].size());k++)
                    ans+=2*nd_size[i][j]*nd_size[i][k];
        }
        printf("%lld\n",ans);
    }
    return 0;
}

正解（C++）