poj3585 Accumulation Degree(树形dp,换根)

题意：

给你一棵n个顶点的树，有n-1条边，每一条边有一个容量z，表示x点到y点最多能通过z容量的水。

你可以任意选择一个点，然后从这个点倒水，然后水会经过一些边流到叶节点从而流出。问你最多你能倒多少容量的水

示例：

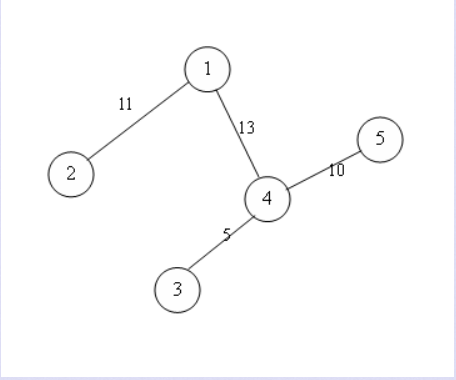
A（1）= 11 + 5 + 8 = 24
详情：1-> 2 11
1-> 4-> 3 5
1-> 4-> 5 8（因为1-> 4的容量为13）
A（2）= 5 + 6 = 11
详细信息：2-> 1-> 4-> 3 5
2-> 1-> 4-> 5 6
A（3）= 5
详细信息：3-> 4-> 5 5
A（4）= 11 + 5 + 10 = 26
详细信息：4-> 1-> 2 11
4-> 3 5
4-> 5 10
A（5）= 10
详细信息：5-> 4-> 1-> 2 10

因为A（4）最大，所以最多能倒26容量的水

题解：

我们可以先随便找一个点当作树根，我这里选择节点1

然后我们可以dfs一遍去获取每一个节点能从它的子节点中的叶节点流出水的量，用数组d来保存

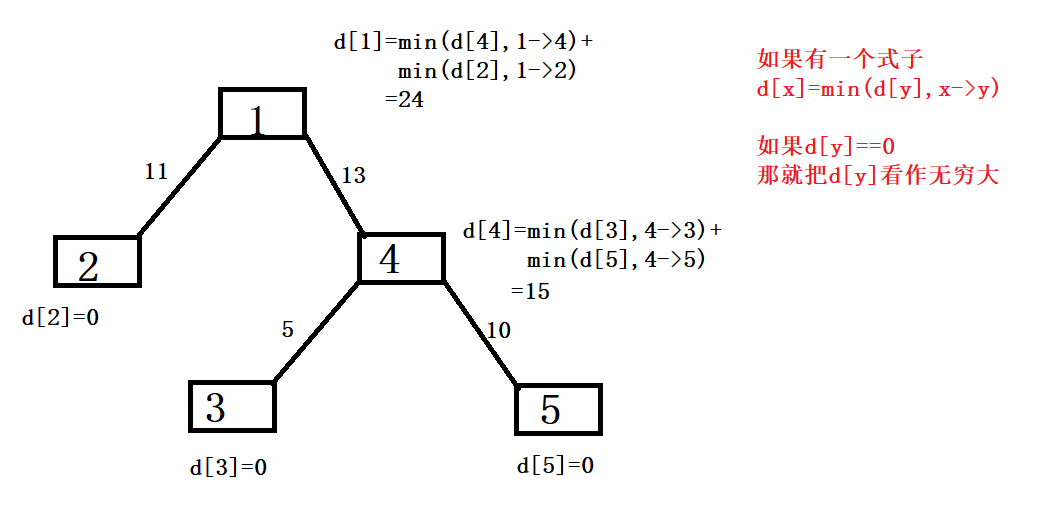
求出来所有节点的d值之后，这个时候1节点的流量就是d[1]，也就是A（1）=d[1]

这个时候我们求A（2）

我们可以先将A（1）减去2节点来的流量

ans=dp[1]-min(1->2,d[2])

然后这个ans和1->2这一条边取最小值，就是不属于2的子节点的其他叶节点能到2节点的流量

这个时候再加上d[2]就可以了

/*
这就是一个树形dp（也就是依据树的边进行dp）
*/
#include<stdio.h>
#include<string.h>
#include<math.h>
#include<algorithm>
#include<iostream>
using namespace std;
#define mem(a) memset(a,0,sizeof(a))
#define mem__(a) memset(a,-1,sizeof(a))
typedef long long ll;
const int maxn=200010;
const int INF=0x3f3f3f3f;
const double blo=(1.0+sqrt(5.0))/2.0;
const double eps=1e-8;
/*
child[x]表示以1为根节点情况下，以x为根的子树上能到达x节点上的最大流
然后你知道dp[x]和child[to]之后就可以求出来dp[to]
因为dp[x]减去从to这个子树上来的流量就是其他节点到x的流量，那么就可以知道其他节点到to节点的流量
 dp[to]=child[to]+min(dp[x]-min(e[i].dis,child[to]),e[i].dis);
 
*/
int n,head[maxn],child[maxn],du[maxn],dp[maxn],num;
struct Edge{
    int next,to,dis;
}e[2*maxn];
void add_edge(int from,int to,int dis){
    e[++num].next=head[from];
    e[num].to=to;
    e[num].dis=dis;
    head[from]=num;
}
int dfs_child(int x,int fa)
{
    int sum=0;
    for(int i=head[x];i!=-1;i=e[i].next)
    {
        int to=e[i].to;
        if(to==fa) continue;
        sum+=min(dfs_child(to,x),e[i].dis);
    }
    child[x]=sum;
    if(du[x]==1) return e[head[x]].dis;
    else return child[x];
}
void dfs(int x,int fa)
{
    for(int i=head[x];i!=-1;i=e[i].next)
    {
        int to=e[i].to;
        if(to==fa) continue;
        /*
        要加这个特判，因为如果我们的1点是一个叶节点（就是我们挑选了一个叶节点为根开始遍历），那么这个叶节点的子节点
        的dp值就需要是加上child[to]，然后再加上父节点的边权，你画个图理解一下
        如果不加这个判断会卡下面这个数据，你按照这个数据画个图
        1
        3
        1 2 1
        2 3 1
        */
        if(du[x]==1) dp[to]=child[to]+e[i].dis;
        else
        dp[to]=child[to]+min(dp[x]-min(e[i].dis,child[to]),e[i].dis);
        dfs(to,x);
    }
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        num=0;
        mem(child);
        mem(dp);
        mem(du);
        mem__(head);
        for(int i=1;i<n;++i)
        {
            int x,y,z;
            scanf("%d%d%d",&x,&y,&z);
            du[x]++;
            du[y]++;
            add_edge(x,y,z);
            add_edge(y,x,z);
        }
        dp[1]=dfs_child(1,-1);
        dfs(1,-1);
        int maxx=0;
        for(int i=1;i<=n;++i)
            maxx=max(maxx,dp[i]);
        printf("%d\n",maxx);
    }
    return 0;
}