布隆过滤器（Bloom Filters）的原理及代码实现（Python + Java）

本文介绍了布隆过滤器的概念及变体，这种描述非常适合代码模拟实现。重点在于标准布隆过滤器和计算布隆过滤器，其他的大都在此基础上优化。文末附上了标准布隆过滤器和计算布隆过滤器的代码实现（Java版和Python版）

本文内容皆来自 《Foundations of Computers Systems Research》一书，自己翻译的，转载请注明出处，不准确的部分请告知，欢迎讨论。

• 布隆过滤器是什么？

  布隆过滤器是一个高效的数据结构，用于集合成员查询，具有非常低的空间复杂度。

   

 

• 标准布隆过滤器（Standard Bloom Filters，SBF）

  基本情况

  布隆过滤器是一个含有 m 个元素的位数组（元素为0或1），在刚开始的时候，它的每一位都被设为0。同时还有 k 个独立的哈希函数 h1, h2,..., hk 。需要将集合中的元素加入到布隆过滤器中，然后就可以支持查询了。说明如下：

  1. 计算h1(x), h2(x),...,hk(x)，其计算结果对应数组的位置，并将其全部置1。一个位置可以被多次置1，但只有一次有效。
  2. 当查询某个元素是否在集合中时，计算这 k 个哈希函数，只有当其计算结果全部为1时，我们就认为该元素在集合内，否则认为不在。
  3. 布隆过滤器存在假阳性的可能，即当所有哈希值都为1时，该元素也可能不在集合内，但该算法认为在里面。
  4. 假阳性出现的概率被哈希函数的数量、位数组大小、以及集合元素等因素决定。

  假阳性率评估

   

  为了评估假阳性率，需要基于一个假设：哈希函数都是完美随机的。约定几个变量：

   

  1. k 哈希函数的数量
  2. n 集合 S 中元素的数量
  3. m 位数组的大小
  4. p 位数组中某一位为0的概率
  5. f 假阳性的概率

  最后得出：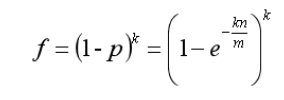

  

   最佳的哈希函数数量

  
  根据数学推理得（过程就算了）：当 p = 1/2, k = ln2 * (m/n)时，f 最小为(1/2)^k
  可以看出，当位数组中有一半零一半一时，结果最好。
  事实上，m 是 n 的倍数，而且 k 常取最接近但小于理论值的整数值。

  部分布隆过滤器（partial bloom filters）

   
   

• 计算布隆过滤器（Counting Bloom Filters，CBF）

  标准的布隆过滤器有一个致命的缺点：不支持删除元素。CBF协议解决的这个问题。

  1. 将标准布隆过滤器中的位数组变成整数数组，即可以用多位表示。
  2. 标准布隆过滤器每个位置可以被多次置1，但只有一次有效，这样，某一个位置被多个元素哈希映射，当要删除其中一个元素时，该元素哈希映射的位置都应该变为零，那么就会破坏其他元素的映射，会出现假阴性。
  3. 由于计算布隆过滤器的数组可以表示更大的整数，那么当某个位置被映射到时，该位置的计数值就自增1，而当某个元素被删除时，就将其映射位置的计数值减1。这样就解决了SBF的问题。
  4. CBF同样存在问题，因为当计数值自增时可能会溢出，当计数值为4比特时，溢出的概率为：1.37 * 10^-15 * m，虽然很低，但对某些应用可能不够。一个简单的解决方法是，当计数值到达最大值时，就不在自增，但这导致假阴性。
   

• 压缩布隆过滤器（Compressed Bloom Filters）

  在网络应用中，布隆过滤器通常被作为信息在各节点间传送，为了节约资源，自然而然就想能不能压缩布隆过滤器后再传送。

  1. 由前面我们知道，要使得布隆过滤器有最小的假阳性概率，数组中包含的0或1的概率应该是一样的，根据香农编码原理（Shannon coding principle），这样的布隆过滤器不能被压缩。虽然这样的布隆过滤器不能被直接压缩，但我们可以用其他方法达到一样的效果。
  2. 要使得布隆过滤器 x 与布隆过滤器 y（ 包含的0或1的概率应该是一样的）具有相同的假阳性概率，那么，x 的大小要大于 y 的，x 的哈希函数的数量不同于 y 的，这样 x 中包含的0和1的数量就不同，x 就可以被压缩。
  3. 问题出来了，压缩布隆过滤器的原因是更节省空间，我们找了个更大的布隆过滤器压缩，那么压缩后的布隆过滤器的空间效率比原布隆过滤器更加优秀吗？是的。
  4. 压缩后，布隆过滤器的本地存储空间会变大，但哈希函数数量会变小（更少的映射操作）、传送的位更少。
   

• D-left 计算布隆过滤器（D-left Counting Bloom Filters）

  上面提到的计算布隆过滤器存在这样的缺点：存储空间是标准布隆过滤器的数倍（取决于计数值的位数）和计数值的不均匀（有些始终为0，有些则可能溢出）。下面看看 D-left Counting Bloom Filters 的特点。D-left Counting Bloom Filters 基于 D-left Hashing。

  D-left Hashing 基本结构

  1. 将一个哈希表分成几个不相交的子表（subtable）
  2. 每个子表里都有数量相同的桶（bucket）
  3. 每个桶里都有一定数量的单元（cell，单元包括特征值和计数值）
  4. 每个单元都是固定的位数组成，用来保存元素的特征值（fingerprint）
  5. 只有一个哈希函数，该哈希函数可以生成和子表数量相同的桶地址和一个特征值

   

  插入操作

  
  假设有 d 个子表，元素为 x，哈希函数为 f

  1. 计算 f(x)，生成桶地址 addr0, addr1, ..., addr(d-1)，特征值 p
  2. 我们检查子表 i 中地址为 addri 的桶中的所有单元（i = 0，1，...，d-1）
  3. 如果某个单元中的特征值和 p 相等，那么元素 x 就在该哈希表中
  4. 若没有找到这样的单元，那么需要找到存储特征值最少的桶（在上面生成的桶地址中找），然后将该特征值 p 随机放入该桶的一个空单元中，该单元的计数值变为1，这考虑了装载平衡

   

  D-left Counting Bloom Filters

  
  由上可知，d-left Hashing 的计数值最大为零，不支持删除操作，为了将它变成可 Counting，可以让它的计数值变成由多位组成。但这样依然会出现问题，如下：

  1. 假设 d-left counting bloom filter 包含 4 个子表，每个子表又包含 4 个桶，初始为空。
  2. 现在有两个元素 x 和 y 需要映射到过滤器中，f(x) = (1, 1, 1, 1，r), f(y) = (1, 2, 3, 4, r)
  3. 已知插如 x 时，第四个子表的第一个桶最空，x 的特征值 r 被插入该桶的某一个单元中，该单元计数值变为1，而插入 y 时，第一个子表的第一个桶最空，y 的特征值 r 被插入该桶的某一个单元中，该单元计计数值变为1
  4. 现在要删除 x，那么就会寻找每个子表的第一个桶中的单元，这时，在第一个子表的第一个桶中找到了特征值 r，接下来就会将该单元的计数值减 1 变为 0，同时，存储的特征值被删除，变为空。
  5. 现在查找 x 是否在表中，结果返回真，而查询 y 是否在表中，结果返回假，导致错误。

  为什么会出现上面的情况？由三个因素促成

  1. x 和 y 有相同的特征值 r
  2. f(x) 和 f(y) 生成的地址有相同的
  3. x 和 y 特征值存储的地方还不一样（存一样就不会出错）

  如何解决？

  说实话，没看懂英文描述的内容。。。。大致是做了排列置换等操作

  性能分析

  比普通的计算布隆过滤器空间少了一半甚至更多，而且效率也有提升（假阳性更低） 

• Spectral Bloom Filters

  Counting Bloom Filters 可以进行元素的删除操作，然而却不能记录一个元素被映射的频率，而且很多应用中元素出现的频率相差很大，也就是说，CBF中每个计数值的位数一样，那么有些计数值很快就会溢出，而另一些则一直都很小。这些问题可以被 Spectral Bloom Filters 解决。

  在SBF中，每一个计数值的位数都是动态改变的。它的构造我没看懂，先留着吧

 

• Dynamic Counting Filters

  Spectral bloom filter 被提出来解决元素频率查询问题，但是，它构造了一个复杂的索引数据结构去解决动态计算器的存储问题。Dynamic counting bloom filter（比SBF好理解多了） 是一个空间时间都很高效的数据结构，支持元素频率查询。相比于SBF，在实际应用中（计数器不是很大，改变不是很频繁时）它有更快的访问时间和更小的内存消耗。

  构成部分

  1. DCBF由两部分组成，第一部分是基础的计算布隆过滤器
  2. 第二部分是一个同样大小的向量，用于记录第一部分中计算器溢出的次数
  3. 第一部分中的计算器位数固定，第二部分中每个溢出计算器位数动态改变

  特点

  1. 当第二部分溢出计算器也面临溢出时，会重新申请一个向量，给要溢出部分增加位数，其他溢出计算器直接拷贝到新的向量中的对应位置，旧的向量会被释放

 

• 学习案例

  Summary Cache
  

      在网络中有极大的资源请求，如果所有的请求都由服务器来处理，网络就会出现拥堵，性能就会下降。所以网络中有大量的中间代理节点。这些代理会把一部分资源放在自己的本地缓存，当用户向服务器请求资源时，该代理先会检查该资源是否在自己的缓存中，如果在就直接发送给用户，否则再向服务器请求。一个代理能够存储的资源是非常有限的，为了进一步减轻服务器的负载，网络中相邻的代理都可以共享自己的缓存。这样，当代理 A 本地缓存没有时，就会向相邻代理广播请求，查询他们是否有该缓存。
      然而，这样依旧有很大问题，假设，这里有 N 个代理，每个代理的命中率为 H，一个代理平均请求 R 次，那么广播中，一个代理收到的查询信息共有 (N-1) * (1-H) * R 条，总共的请求也就是 
  N * (N-1) * (1-H) * R。这是非常低效的。
      再次改进，各个代理之间交换自己缓存的摘要信息。这样，当代理 A 失败后，会先查询各个代理的摘要信息，然后决定是定向向某个代理请求，还是向服务器请求资源。这就大大的减少了网络通信量。为了满足快速查询、更新摘要信息，一个非常好的选择就是计算布隆过滤器（Counting bloom filters）。
  
  

  IP Traceback
  

     网络中存在许多攻击，有时候需要根据一些数据包去还原IP路径，找到攻击者。一个可行的办法是在路由器中存储数据包信息。然而，有些网络中通信量巨大，存储所有的包是不现实的，因此可以存储这些包的摘要信息。这时，选用布隆过滤器可以极大的节省空间，而且具有非常快的查询。

   

• 代码实现

标准布隆过滤器构建、测试代码（Python 面向过程版）

 import math
 import random
 import time

 def hash_function(a, b, c, item, tablelen):
     return (a * item ** 2 + b * item + c) % tablelen  #哈希函数

 def construction_of_SBF(tablelen = 1000, set = []):

     k = int(math.log(2, math.e) * (tablelen / len(set)))
     hash = []
     random.seed(time.time())
     for i in range(k):  #随机生成哈希函数的三个参数
         a = random.randint(1, 1000)
         b = random.randint(1, 1000)
         c = random.randint(1, 1000)
         hash.append((a, b, c))

     bitArray = [0] * tablelen

     for element in set:     #映射集合元素到位数组
         for i in range(k):
             hx = hash_function(hash[i][0], hash[i][1], hash[i][2], element, tablelen)
             bitArray[hx] = 1

     filter = [bitArray, hash]
     return filter

 # 测试
 def test_bloom_filters(bloom_filter = None):
     if bloom_filter == None:
         return False

     testSet = [1, 3, 7, 111, 99, 54, 34, 67, 81, 121, 101, 100, 23, 0, 845, 3339, 44]
     for item in testSet:
         flag = True
         for i in range(len(filter[1])):
             hx = hash_function(filter[1][i][0], filter[1][i][1], filter[1][i][2], item, len(filter[0]))
             if bloom_filter[0][hx] != 1:
                 flag = False
                 break

         if flag is True:
             print("%d is in filter\n" % item)
         else:
             print("%d is not in filter\n" % item)

     return True

 if __name__ == "__main__":
     filter = construction_of_SBF(set = list(range(10)))
     test_bloom_filters(filter)

计算布隆过滤器构建、测试代码（Python 面向过程版）

 import math
 import random
 import time

 """
 结构没有设置好，按下写：
 0. 封装函数
 1. 哈希函数：计算哈希值
 2. 生成哈希随机参数函数
 3. 插入函数：被调用
 4. 删除函数：被调用
 5. 查询函数：测试函数调用
 6. 测试函数：测试插入和删除

 """

 def hash_function(params, item, tlen):
     return (params[0] * item ** 2 + params[1] * item + params[2]) % tlen

 def deletion_counting_bloom_filter(cbfilter = None, item = None):
     if (cbfilter is None) or (item is None):
         return False
     for params in cbfilter[2]:
         cbfilter[0][hash_function(params, item, len(cbfilter[0]))] -= 1
     return True

 def insertion_counting_bloom_filter(item = None, cbfilter = None):
     if (item == None) or (cbfilter == None):
         return False
     for params in cbfilter[2]:
         cbfilter[0][hash_function(params, item, len(cbfilter[0]))] += 1
     return True

 def query_counting_bloom_filter(item = None, cbfilter = None):
     for params in cbfilter[2]:
         if(cbfilter[0][hash_function(params, item, len(cbfilter[0]))]) is 0:
             return False
     return True

 def construction_counting_bloom_filter(filterSet = None, filterArray = None):
     if (filterSet is None) or (filterArray is None):
         return None
     # 最佳的哈希函数数量
     hashNum = int(math.log(2, math.e) * (len(filterArray) / len(filterSet)))
     hashParam = []
     random.seed(time.time())
     # 随机生成哈希参数
     for i in range(hashNum):
         a = random.randint(1, 9999)
         b = random.randint(1, 9999)
         c = random.randint(1, 9999)
         hashParam.append((a, b, c))

     # 将初始集合元素映射到过滤器数组中
     for item in filterSet:
         for params in hashParam:
             filterArray[hash_function(params, item, len(filterArray))] += 1

     # 返回过滤器数组、过滤器集合、过滤器哈希参数
     return (filterArray, filterSet, hashParam)

 def test_counting_bloom_filters(cbfilter = None):
     if cbfilter is None:
         return None
     testSet = cbfilter[1][10:20]

     # 先测试原有元素是否正常映射
     for item in testSet:
         if query_counting_bloom_filter(item, cbfilter) is True:
             print("%d is in filter\n" % item)
         else:
             print("%d is not in filter\n" % item)

     # 删除后再查询
     if deletion_counting_bloom_filter(cbfilter, testSet[0]) is True:
         print("delete successfully!\n")
     else :
         print("delete fails\n")

     if query_counting_bloom_filter(testSet[0], cbfilter) is True:
         print("%d is in filter\n" % testSet[0])
     else :
         print("%d is not in filter\n" % testSet[0])

     # 插入后再测试
     if insertion_counting_bloom_filter(testSet[0], cbfilter) is True:
         print("insert %d successfully\n" % testSet[0])
     else:
         print("insert %d fails\n")

     if query_counting_bloom_filter(testSet[0], cbfilter) is True:
         print("%d is in filter\n" % testSet[0])
     else :
         print("%d is not in filter\n" % testSet[0])

 # 封装后的函数
 def counting_bloom_filters(filterSet = None, filterArray = None):
     if (filterSet is None) or (filterArray is None):
         return False
     # 构造：初始集合元素的映射、哈希函数参数生成
     cbfilter = construction_counting_bloom_filter(filterSet, filterArray)

     # 测试：测试插入、删除、查询
     test_counting_bloom_filters(cbfilter)

 if __name__ == "__main__":
     filterSet = list(range(100))
     filterArray = [0] * 10000
     counting_bloom_filters(filterSet, filterArray)

标准布隆过滤器构建、测试代码（Java 面向对象版）

 // package BloomFilters;

 import java.util.Arrays;
 import java.util.Random;
 import java.io.*;
 import java.math.BigInteger;
 import java.nio.*;
 import java.nio.charset.StandardCharsets;
 import java.nio.file.Path;
 import java.util.*;

 /**
  * 实现标准布隆过滤器的类
  */
 public class SBFilters {
     // 实例字段
     private boolean[] bitArray; //位数组
     private int[][] hashParams; //随机的哈希函数参数

     // 方法字段
     public SBFilters(int tLen, int[] iSet)
     {
         this.bitArray = new boolean[tLen];
         Arrays.fill(this.bitArray, Boolean.FALSE);
         this.construction_filter(iSet);
     }

     private boolean construction_filter(int[] iSet)
     {
         if(iSet == null || iSet.length == 0)
         {
             return false;
         }
         var hashNum = (int)(Math.log(2) * (this.bitArray.length / iSet.length));
         this.construction_hashParams(hashNum);
         for(var item: iSet)
         {
             for(var params: this.hashParams)
             {
                 this.bitArray[hash_function(params, item)] = true;
             }
         }
         return true;
     }

     private boolean construction_hashParams(int hashNum)
     {
         this.hashParams = new int[hashNum][3];
         var time = System.currentTimeMillis();
         var rd = new Random(time);
         for(int i = 0; i < hashNum; i++)
         {
             this.hashParams[i][0] = rd.nextInt(9999) + 1;
             this.hashParams[i][1] = rd.nextInt(9999) + 1;
             this.hashParams[i][2] = rd.nextInt(9999) + 1;
         }
         return true;
     }

     private int hash_function(int[] params, int item)
     {
         return (int)((params[0] * Math.pow(item, 2.0) +
             params[1] * item + params[2]) % bitArray.length);
     }

     public boolean query_filter(int item)
     {
         for(var params: this.hashParams)
         {
             if(this.bitArray[hash_function(params, item)] == false)
             {
                 return false;
             }
         }
         return true;
     }

 }

 // package BloomFilters;

 /**
  * 用来测试实现的布隆过滤器是否正常工作
  */
 public class FiltersTest
 {
     public static void main(final String[] args)
     {
         test_counting_bloom_filters();
     }

     private static void test_counting_bloom_filters()
     {
         var iSet = new int[10000];
         for(int i = 0; i < 10000; iSet[i] = i++);
         SBFilters sbFilter = new SBFilters(999999, iSet);

         for(var item: new int[]{1, 3, 5, 78, 99, 100, 101, 9999, 10000, 3534})
         {
             var isIn = sbFilter.query_filter(item);
             if(isIn == false)
             {
                 System.out.printf("%d is not in the filter\n", item);
             }
             else
             {
                 System.out.printf("%d is in the filter\n", item);
             }
         }
     }

 }