数理统计5：指数分布的参数估计，Gamma分布，Gamma分布与其他分布的联系

今天的主角是指数分布，由此导出\(\Gamma\)分布，同样，读者应尝试一边阅读，一边独立推导出本文的结论。由于本系列为我独自完成的，缺少审阅，如果有任何错误，欢迎在评论区中指出，谢谢！

目录

• Part 1：指数分布的参数估计
• Part 2：独立同分布指数分布之和与$\Gamma$分布
• Part 3：$\Gamma$分布与其他分布

Part 1：指数分布的参数估计

指数分布是单参数分布族，总体\(X\sim E(\lambda)\)有时也记作\(\mathrm{Exp}(\lambda)\)，此时的总体密度函数为

\[f(x)=\lambda e^{-\lambda x}I_{x>0}.
\]

现寻找其充分统计量，样本联合密度函数为

\[\begin{aligned}
f(\boldsymbol{x})&=\lambda^n\exp\left\{-\lambda\sum_{j=1}^n x_j \right\}I_{x_1>0}\cdots I_{x_n>0}\\
&=\lambda^ne^{-n\lambda \bar x}I_{x_{(1)}>0},
\end{aligned}
\]

由因子分解定理，取

\[g(\bar x,\lambda)=\lambda^ne^{-n\lambda \bar x},\quad h(\boldsymbol{x})=I_{x_{(1)}>0},
\]

可以得到\(\bar X\)是\(\lambda\)的充分统计量。但是指数分布的参数并非均值，而是均值的倒数，所以对\(\bar X\)也有

\[\mathbb{E}(\bar X)=\mathbb{E}(X)=\frac{1}{\lambda}.
\]

注意，千万不要想当然地认为期望和一般的函数之间是可交换的，即一般来说\(\mathbb{E}[f(X)]\ne f[\mathbb{E}(X)]\)，所以你不能认为\(\bar X^{-1}\)就是\(\lambda\)的无偏估计量。

每到此时，我就想举对数正态分布的例子：\(X\sim N(0,\sigma^2)\)，求\(e^{X}\)的期望。显然有

\[\begin{aligned}
\mathbb{E}(e^{X})&=\int_{-\infty}^\infty e^x\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left\{-\frac{x^2}{2\sigma^2} \right\}\mathrm{d}x\\
&=\int_{-\infty}^\infty \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left\{-\frac{x^2-2\sigma^2x}{2\sigma^2} \right\}\mathrm{d}x\\
&=e^{-\frac{\sigma^2}{2}}\int_{-\infty}^\infty \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left\{-\frac{(x-\sigma^2)^2}{2\sigma^2} \right\}\mathrm{d}x\\
&=e^{-\frac{\sigma^2}{2}}.
\end{aligned}
\]

最后一个等号处，积分是\(N(\sigma^2,\sigma^2)\)的密度函数全积分为1。这说明

\[\mathbb{E}(e^{X})=e^{-\frac{\sigma^2}{2}}\ne 1=e^{\mathbb{E}(X)}.
\]

同样，也能告诉我们股票的波动率越大，期望收益也越大。

但是，用\(\bar X^{-1}\)总是有一定道理的，至少在量级上保持了跟待估参数的一致性。如果我们要进行无偏调整，则需要求出\(\bar X\)的具体密度。不妨设\(T=\sum_{j=1}^n X_j\)，则\(T=n\bar X\)，如果我们能求出\(T\)的分布，也一样能得出\(\bar X^{-1}\)的期望。

Part 2：独立同分布指数分布之和与\(\Gamma\)分布

为求\(T\)的分布，引入一个Jacobi行列式为1的线性变换：

\[\left\{\begin{array}l
Y_{1} = X_{1}, \\
Y_{2}=X_{2},\\
\vdots \\
Y_{n-1}=X_{n-1}, \\
Y_{n}=X_{1}+\cdots+ X_{n}.
\end{array}\right.
\]

则\((Y_{1},\cdots,Y_{n})\)的联合密度函数为

\[\begin{aligned}
f_{Y}(\boldsymbol{y})&=f_X(y_{1},\cdots,y_{n-1},y_n-y_{n-1}-\cdots-y_1)\\
&=\lambda^n\exp\left\{-\lambda\left[\sum_{j=1}^{n-1}y_j+\left(y_n-\sum_{j=1}^{n-1}y_j \right) \right] \right\}I_{y_1>0}\cdots I_{y_{n-1}>0}I_{y_n>\sum_{j=1}^{n-1}y_j}\\
&=\lambda^n e^{-\lambda y_n}I_{y_1>0}\cdots I_{y_{n-1}>0}I_{y_n>\sum_{j=1}^{n-1}y_j}.
\end{aligned}
\]

接下来要依次对\(y_1,\cdots,y_{n-1}\)作积分，为方便计，记

\[\mathcal B_k=y_n-\sum_{j=k}^{n-1}y_j,\quad k=1,2,\cdots,n-1,\\
\mathcal B_{k+1}-\mathcal B_{k}=y_k.
\]

现在，\(y_1\)的积分范围是\((0,y_n-y_{n-1}-\cdots-y_2)=(0,\mathcal B_2)\)，即

\[f_{Y_2,\cdots,Y_n}(y_2,\cdots,y_n)=\lambda^ne^{-\lambda y_n}\mathcal B_2I_{y_2>0}\cdots I_{y_{n-1}>0}I_{\mathcal B_2>0}.
\]

再对\(y_2\)积分，其积分范围是\((0,\mathcal B_3)\)，即

\[\begin{aligned}
&\quad f_{Y_3,\cdots,Y_n}(y_3,\cdots,y_n)\\
&=\lambda ^ne^{-\lambda y_n}\int_{0}^{\mathcal B_3}\mathcal B_2\mathrm{d}y_2\\
&=\lambda^ne^{-\lambda y_n}\int_0^{\mathcal B_3}(\mathcal B_3-y_2)\mathrm{d}y_2\\
&=\lambda^n e^{-\lambda y_n}\cdot\frac{\mathcal B_3^2}{2}I_{y_3>0}\cdots I_{y_{n-1}>0}I_{\mathcal B_3>0}.
\end{aligned}
\]

继续下去的步骤就很机械了，对\(y_3\)积分时积分范围是\((0,\mathcal B_4)\)，所以

\[\begin{aligned}
&\quad f_{Y_4,\cdots,Y_n}(y_4,\cdots,y_n)\\
&=\frac{1}{2}\lambda^n e^{-\lambda y_n}\int_0^{\mathcal B_4}[\mathcal B_4-y_3]^2\mathrm{d}y_3\\
&=\frac{1}{2}\lambda^n e^{-\lambda y_n}\int_0^{\mathcal B_4}[\mathcal B_4-y_3]^2\mathrm{d}(\mathcal B_4-y_3)\\
&=\frac{1}{2\cdot 3}\lambda^n e^{-\lambda y_n}\mathcal B_4^3I_{y_4>0}\cdots I_{y_{n-1}>0}I_{\mathcal B_4>0}.
\end{aligned}
\]

将这个过程一直进行下去，容易得到

\[f_{Y_{n-1},Y_n}(y_{n-1},y_n)=\frac{1}{(n-2)!}\lambda^ne^{-\lambda y_n}\mathcal B_{n-1}^{n-2}I_{y_{n-1}>0}I_{y_n>y_{n-1}},
\]

进行最后一次积分就能得到\(T\)的密度函数为

\[f_T(x)=\frac{1}{(n-1)!}\lambda^ne^{-\lambda x}x^{n-1}.
\]

这里有一个稍微有点耍赖的技巧。如果你不想一个个积分，而又记住了指数分布和的密度函数形式，则可以用数学归纳法验证指数分布和的密度函数恰有如此的形式。

读者可以自行用数学归纳法计算一遍，这个计算量是比较小的。

同样，我们以后会经常跟这个密度函数打交道。因为阶乘只适用于整数，将其解析延拓到\(\mathbb{R}^+\)上有\((n-1)!=\Gamma(n)\)，注意到其核为\(e^{-\lambda x}x^{n-1}\)，对于任意\(n>0,\lambda >0\)，有

\[\int_0^{\infty}e^{-\lambda x}x^{n-1}\mathrm{d}x=\int_0^{\infty}\frac{1}{\lambda^n}e^{-\lambda x}(\lambda x)^{n-1}\mathrm{d}(\lambda x)=\frac{\Gamma(n)}{\lambda ^n},
\]

所以其正则化因子为\(\frac{\lambda^n}{\Gamma(n)}\)。现在我们可以正式给出\(\Gamma\)分布的定义：称\(X\sim\Gamma(n,\lambda)\)，如果\(X\)具有如下的密度函数：

\[p(x)=\frac{\lambda^n}{\Gamma(n)}x^{n-1}e^{-\lambda x}.
\]

当\(n\)为整数时，\(\Gamma(n)=(n-1)!\)。同时，我们得到一个重要结论：若\(X_1,\cdots,X_n\stackrel{\mathrm{i.i.d.}}\sim E(\lambda)\)，则

\[T=\sum_{j=1}^n X_j\sim \Gamma(n,\lambda).
\]

Tlst <- c()
for (i in 1:100000){
  Tlst[i] <- sum(rexp(5, 3))  # T为5个E(3)样本之和
}

plot(density(Tlst), main = "T的样本密度", col = "blue", xlim = c(0, 6))
xlst <- seq(0, 6, 0.00001)
ylst <- dgamma(xlst, 5, 3)
lines(xlst, ylst, col = "red")

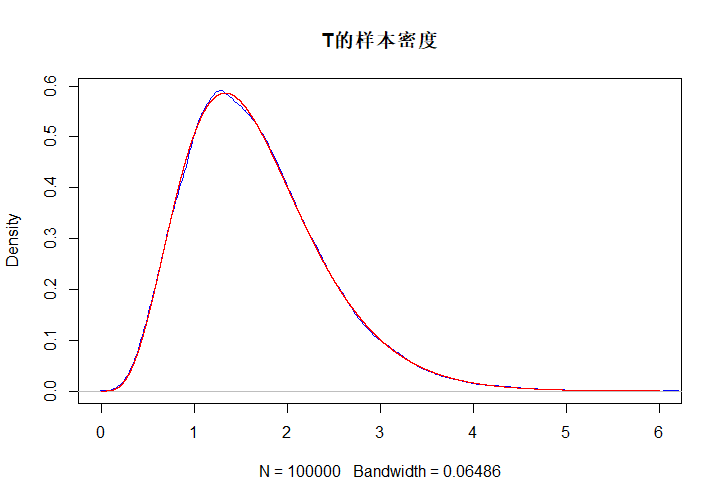
由于\(\Gamma\)分布核函数的特点，其期望和方差也是容易求出的。现设\(X\sim \Gamma(n)\)，则

\[\mathbb{E}(X)=\int_0^{\infty}\frac{\lambda^n}{\Gamma(n)}x^ne^{-\lambda x}\mathrm{d}x=\frac{\Gamma(n+1)}{\lambda\Gamma(n)}\int_0^{\infty}\frac{\lambda^{n+1}}{\Gamma(n+1)}x^{n+1-1}e^{-\lambda x}\mathrm{d}x=\frac{n}{\lambda}.
\]

这说明\(n\)越大\(X\)的期望越大，\(\lambda\)越大\(X\)的期望越小，如果将其视为独立指数分布的和也能得到这个结论。

\[\mathbb{E}(X^2)=\frac{\Gamma(n+2)}{\lambda^2\Gamma(n)}=\frac{n(n+1)}{\lambda^2},\\
\mathbb{D}(X)=\mathbb{E}(X^2)-[\mathbb{E}(X)]^2=\frac{n}{\lambda^2}.
\]

现在回到正题，计算指数分布均值倒数\(\bar X^{-1}\)的期望，先计算\(T^{-1}\)的期望，容易计算得到

\[\mathbb{E}(T^{-1})=\int_0^{\infty}\frac{\lambda ^n}{\Gamma(n)}x^{n-2}e^{-\lambda x}\mathrm{d}x=\frac{\lambda\Gamma(n-1)}{\Gamma(n)}=\frac{\lambda}{n-1},
\]

因此自然有

\[\mathbb{E}\left(\frac{1}{\bar X} \right)=\mathbb{E}\left(\frac{n}{\bar X} \right)=\frac{\lambda n}{n-1}.
\]

因此，\(\bar X^{-1}\)只是\(\lambda\)的渐进无偏估计，可以对它经过无偏处理得到无偏估计：

\[\hat\lambda(\boldsymbol{X})=\frac{n-1}{n\bar X}.
\]

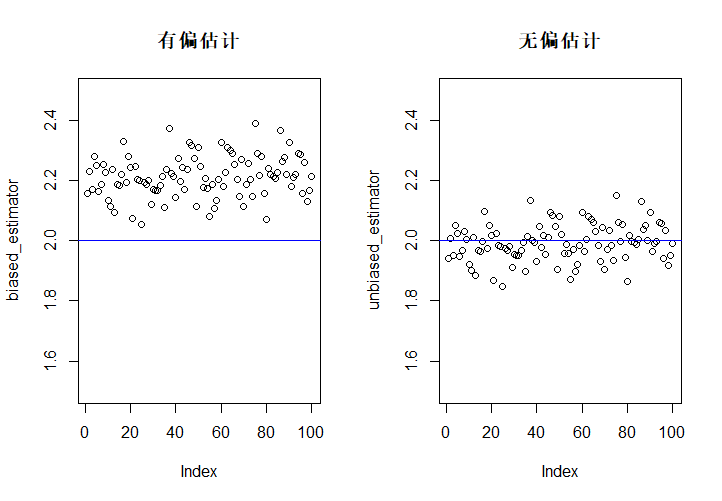
下面进行\(\hat \lambda\)的有偏估计、无偏估计的模拟计算，从指数分布\(E(2)\)中抽样。为了体现出区别，图中的每一个点都是100个估计量的平均值。

rm(list = ls())
unbiased_estimator <- c()
biased_estimator <- c()
for (j in 1:100){
  meanlst <- c()
  for (i in 1:100){
    samples <- rexp(10, 2)  # 每次产生10个样本计算均值
    meanlst[i] <- 1/mean(samples)
  }
  biased_estimator[j] <- mean(meanlst)
  unbiased_estimator[j] <- 9/10*biased_estimator[j]
}

split.screen(c(1, 2))
screen(1)
plot(biased_estimator, main = "有偏估计", ylim = c(1.5, 2.5))
abline(h = 2, col = "blue")

screen(2)
plot(unbiased_estimator, main = "无偏估计", ylim = c(1.5, 2.5))
abline(h = 2, col = "blue")

Part 3：\(\Gamma\)分布与其他分布

\(\Gamma\)分布与许多分布具有紧密的联系（中心极限定理这种与正态分布的联系就不说了）。与指数分布的联系是显然的：\(\Gamma(1,\lambda)\)就是\(E(\lambda)\)，这点从上面的推导可以得出。

需要注意一点：指数分布的参数是其尺度参数。什么意思呢？对于\(X\sim E(\lambda)\)，它的分布函数是\(F(x)=1-e^{-\lambda x}\)，对其作伸缩变换\(aX\)，有

\[F_{aX}(x)=\mathbb{P}(aX<x)=F\left(\frac{x}{a} \right)=1- e^{-\frac{\lambda x}{a}},
\]

对比\(F(x)\)的形式，发现\(aX\sim E(\lambda /a)\)，这就代表伸缩变换不改变指数分布的性质，所以说指数分布的参数是其尺度参数。既然\(\Gamma\)分布是指数分布的直接推广，则\(\Gamma\)分布也具有这样的性质：若\(X\sim \Gamma(n,\lambda)\)，则

\[aX\sim \Gamma\left(n,\frac{\lambda }{a} \right).
\]

这样的变换不改变数量参数\(n\)，这也是指数分布中得到的直接推广结论。

还记得正态分布的衍生分布——\(\chi^2(n)\)分布吗？之前，因为卡方分布的密度函数过于复杂，不好记忆，所以我们跳过了，但了解过\(\Gamma\)分布的密度函数后再回看卡方分布，就会有一种熟悉感。

对于\(X\sim \chi^2(n)\)，其密度函数为

\[p(x)=\frac{1}{2^{n/2}\Gamma(n/2)}x^{\frac{n}{2}-1}e^{-\frac{x}{2}},
\]

可以看到，它的核刚好是\(e^{-x}\)的某次方，乘以\(x\)的某次方形式，前面的正则化系数由核决定，因此，\(\chi^2(n)\)分布本质上也是\(\Gamma\)分布的一种特例，即

\[X\sim \Gamma\left(\frac{n}{2},\frac{1}{2} \right).
\]

这样，再记忆\(\chi^2(n)\)分布的密度函数就会显得容易一些了。另外，如果\(2n\)是整数，也可以通过\(\Gamma\)分布的伸缩变换将其变成卡方分布：

\[X\sim \Gamma(n,\lambda)\Rightarrow 2\lambda X\sim \Gamma\left(n,\frac{1}{2} \right)=\chi^2(2n),\\
X\sim E(\lambda)\Rightarrow 2\lambda X\sim \chi^2(2).
\]

最后，由于我们接下来要进入离散分布的参数估计，在这里也给出一个\(\Gamma\)分布与泊松分布的联系，这个联系在随机过程中会发挥一定的作用，其证明在数理统计中倒不是特别重要。

若\(N\)定义为满足下列条件的\(n\)值：\(X_1,X_2,\cdots\stackrel{\mathrm{i.i.d.}}\sim E(\lambda)\)，

\[\sum_{j=1}^n X_j\le 1<\sum_{j=1}^{n+1}X_j
\]

则\(N\sim P(\lambda)\)。

下面给出这个定理的证明，其中的思想可以学习。

设\(\sum_{j=1}^k X_j\)的密度函数为\(p_k(x)\)，则由于\(\sum _{j=1}^k X_j\sim \Gamma(k,\lambda)\)，所以

\[p_k(x)=\frac{\lambda^k}{\Gamma(n)}x^{k-1}e^{-\lambda x}.
\]

由全概率公式（连续形式），

\[\begin{aligned}
&\quad \mathbb{P}(N=k)\\
&=\mathbb{P}\left(\sum_{j=1}^kX_i\le 1,\sum_{j=1}^{k+1}X_i>1 \right)\\
&=\int_0^1\mathbb{P}\left(\sum_{j=1}^{k+1} X_j>1\bigg|\sum_{j=1}^k X_i=x \right)p_k(x)\mathrm{d}x\\
&=\int_0^1\mathbb{P}(X_{k+1}>1-x)p_k(x)\mathbb{d}x\\
&=\int_0^1e^{-\lambda {(1-x)}}\frac{\lambda^k}{(k-1)!}x^{k-1}e^{-\lambda x}\mathrm{d}x\\
&=\frac{\lambda^k e^{-\lambda}}{(k-1)!}\int_0^1 x^{k-1}\mathrm{d}x\\
&=\frac{\lambda^k}{k!}e^{-\lambda}.
\end{aligned}
\]

这是泊松分布的分布列，故\(N\sim P(\lambda)\)。

---

在上面两篇文章中，将连续分布的点估计进行了详细的讨论，并引出了次序统计量的分布，介绍了\(\Gamma\)分布与\(\beta\)分布。接下来，我们将转向离散型分布的参数点估计，看看离散形式下因子分解定理应当如何使用。