洛谷 CF1012C Hills（动态规划）

题目大意：

　　有几座山，如果一座山左右两边的山比它矮，那么可以在这个山上建房子，你有一台挖掘机，每天可以挖一座山一米，问你需要花多少代价可以分别盖1、2、3……座房子。（给出山的数量，以及每座山的高度）。

题目分析：

　　性质1：不会有两座相邻的山都建房子。性质 2：一座山盖房子就不会被挖，被挖就不会盖房子（两条废话）

　　每一座山有两种情况：建房子或者不建，可以用一维来保存（[ 0 ]/[ 1 ]）。

　　1到第 i 座山的代价和只与 i 前面的两座山有关：如果这座山（ i ）不建，那么他前面那座山( i-1 )可建可不建，它的代价就是前面山代价的最小值。如果这座山(i)建房，那么它前面的那座山（i - 1）一定不建，它的代价就与前两座山有关系。以此类推，就可以遍历全部求最值。

　　我们定义一个数组dp[ i ] [ j ] [0/1 ]用来表示前 i 座山中建了 j 个房子的代价 ，最后一维表示当前第 i 座山是否建房子。

　　如果这座山选择不盖房子，那么它的代价取决于前一座山的情况。

　　

　　如图：

　　

dp[i][j][0]=min(dp[i-1][j][0],dp[i-1][j][1]+cost(i-1,i));//如果前一座山盖房子，那么这座山有可能挖

cost(i，j)函数表示 i 盖房子需要挖 j 挖多少代价。

int cost(int i,int j){
    if(a[j]>=a[i]){
        return a[j]-a[i]+1;
    }else{
        return 0;
    }
}

如果这座山盖房子：

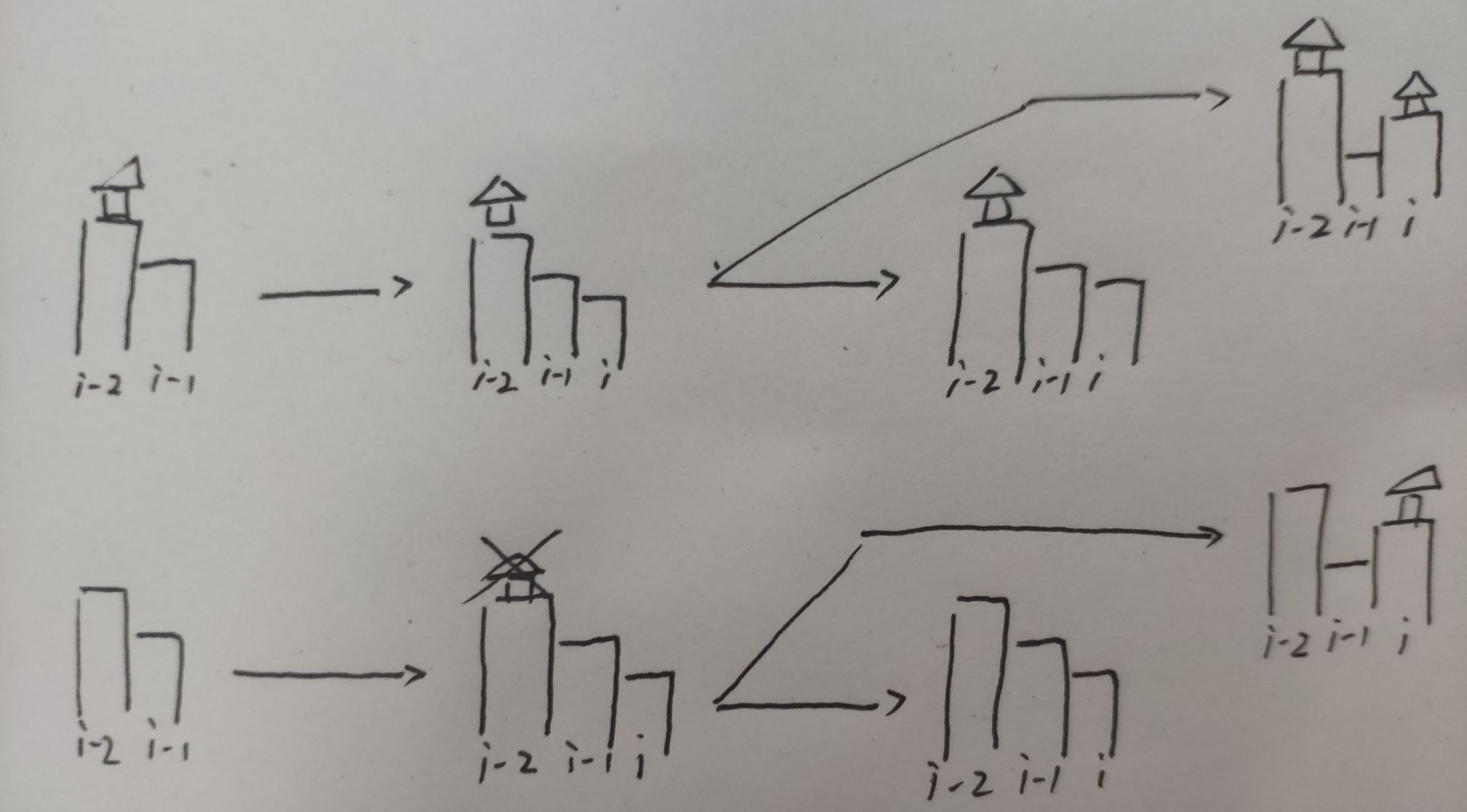
如图，这座山的代价与前面两座山都有关。

如果 i 选择盖房子，那么 i - 1 肯定盖不了，而 i - 2盖不盖房子会产生影响。

如果 i - 2 不盖房子，那就没什么可以担心的，直接挖 i - 1 到比 i 矮就可以了。

如果 i - 2 盖房子，那就要比较到底把 i - 1 挖到比谁矮。

dp[i][j][1]=min(dp[i-2][j-1][0]+cost(i,i-1),dp[i-2][j-1][1]+max(cost(i,i-1),cost(i-2,i-1)));

最后要输出的结果，是盖 1，2，3，……栋房子的最小代价。

首先我们需要知道最多盖几栋房子:

　　设想：一共n座山，相邻山不能同时盖房子，所以要么盖1、3、5、7……要么盖2、4、6、8……

　　最多盖（ n + 1 ）/2栋房子（自己推一下，记住整形运算自动向下取整）

这样结果就出来了，输出相应的 min(dp[ i ][ j ][ 0 ],dp[ i ][ j ][ 1 ])即可。

全代码：

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn=5010;
int dp[maxn][maxn][2],a[maxn];
int cost(int i,int j){
    if(a[j]>=a[i]){
        return a[j]-a[i]+1;
    }else{
        return 0;
    }
}
int n,cnt;
int main(){
        scanf("%d",&n);
        for(int i=1;i<=n;i++){
            a[i]=0;
            for(int j=1;j<=n;j++){
                dp[i][j][0]=dp[i][j][1]=0x3fffffff;
            }
        }
        for(int i=1;i<=n;i++){
            scanf("%d",&a[i]);
        }
        dp[1][1][1]=0;
        dp[2][1][1]=cost(2,1);
        dp[2][1][0]=cost(1,2);
        for(int i=3;i<=n;i++){
            for(int j=1;j<=i;j++){
                dp[i][j][0]=min(dp[i-1][j][0],dp[i-1][j][1]+cost(i-1,i));
                dp[i][j][1]=min(dp[i-2][j-1][0]+cost(i,i-1),dp[i-2][j-1][1]+max(cost(i,i-1),cost(i-2,i-1)));

                if(2*j>=i)break;
            }
        }
        int cnt=(n+1)/2;
        for(int j=1;j<=cnt;j++){
            printf("%d ",min(dp[n][j][1],dp[n][j][0]));
        }
        printf("\n");

}