贪心思想之区间贪心 关联洛谷P1803

力扣上也有一道类似的题 几乎是一样 输出不同 → 力扣leetcode 435. 无重叠区间

区间贪心是比较经典的 就拿洛谷P1803来举例

题目大意

n个比赛 [开始时间，结束时间] 问一个人最多能参加几个（不能同时参加两个且必须有始有终）

题解

首先考虑最简单的情况，如果区间L1被区间L2包含（图a），那么显然选择L1是最好的，也符合局部贪心思想。
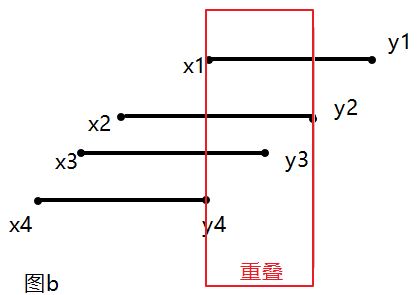
然后把所有区间按左端点（此例子就是开始时间）从大到小排序，如果把重叠的区间去除了，必然得到的是y1>y2>...>yn（图b）
所以选择的时候，以y1为第一个选择的，去除重叠部分后，下一个只能选择y4，因此总是选择端点最大的区间进行比较可以是左端点从大到小排序，也可以是从右端点开始

Show me the code

#include <bits/stdc++.h> //万能头文件
using namespace std;
const int maxn = 1000000;
struct inteval{
    int s, e; //开始s 结束e
}I[maxn];

bool cmp(inteval a, inteval b){
    if(a.s != b.s) return a.s > b.s; // 先按开始时间从大到小排序
    else return a.e < b.e; // 开始时间相同时按结束时间从小到大排序
}

int main(){
    int n;
    cin >> n;
    for (int i = 0; i < n; i++)
        cin >> I[i].s >> I[i].e ;
    sort(I, I + n, cmp); // 区间排序
    // ans 记录不相交区间 也就是能同时得到的区间
    // lastS 记录上一个选中区间的开始端点
    int ans = 1, lastS = I[0].s;
    for (int i = 1; i < n; i++){
        if(I[i].e <= lastS){ // 如果该区间的右端点（结束时间）在lastS左边
            lastS = I[i].s; // 以I[i] 作为新选中的区间
            ans ++; // 不想交数 ++
        }
    }
    cout << ans;
    return 0;
}