分贝单位的本质（下半篇），dBm、dBFS、dBV的妙处你想象不到

上半篇讲到了声音分贝的概念，

对于声音的单位：dB SPL和dB SIL，有兴趣了解并推算的朋友，可以点击以下链接（PC端效果更佳）

http://www.sengpielaudio.com/calculator-soundlevel.htm

下面我们进入正题。

功率和电压的dB的区别

在上半篇里说过了，关于dB最初的单位是用来描述功率（单位瓦特）的。那么当初功率的相对值为什么要用dB描述呢？再一次列一下公式：

\(L_{dB} = 10 \times \log_{10}\frac{P1}{P0}\)

注意P1和P0的单位都是瓦。在上半篇说，dB可以形容声音。那么在电子工程中，dB既然可以形容功率了，那么dB也应该可以形容电压。当dB用来形容电压时的功率是这样的：

\(L_{dB} = 10 \times \log_{10}(\frac{U1}{U0})^{2}\)

注意U1和U0都是电压，单位都是伏特。哎呀我擦，怎么就莫名其妙就多了个平方呢？

这个时候初中物理老师又出来了，ta告诉了我们：

\(P = \frac{{U}^{2}}{R}\)

把这个公式代到上述的那个公式中：

\(L_{dB} = 10 \times \log_{10}\frac{P1}{P0}\)

可得：

\(L_{dB} = 10 \times \log_{10}\frac{\frac{{U1}^{2}}{R}}{\frac{{U2}^{2}}{R}} = 10 \times \log_{10}(\frac{U1}{U0})^{2}\)

这还没完，初高中数学老师出来了，ta说：

\(L_{dB} = 10 \times \log_{10}(\frac{U1}{U0})^{2} = 20 \times \log_{10}\frac{U1}{U0}\)

所以当P1/P0是2的时候，也就是P1比P0的功率大一倍的时候，算得约等于是3dB，此时P1比P0大3dB。

而当U1/U0是2的时候，也就是U1比U0的电压大一倍的时候，算得约等于是6dB，此时U1比U0大6dB。

哎呀我擦，dB你这小伙子你还有两副嘴脸……

dB在电子工程中的好处都有啥

为啥贝尔大佬这么喜欢用log10，这是有好处的，比如在电子中最常出现的功率放大器，如下：

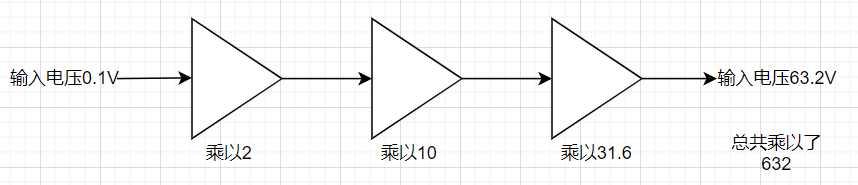
上面的这张图，从一开始的输入电压到最后的输出电压，放大的倍数是632倍。这里使用了乘法，如果放大器太多了，那么我们需要拿出计算器出来慢慢乘，有点不方便。

这个时候初高中数学老师又跳出来了！ta说了，log的运算法则是这样的：

\(20\log_{10}({M1}\times{M2}) = 20\log_{10}{M1} + 20\log_{10}{M2}\)

以上的M1和M2都是放大倍数，如果两个放大倍数相乘的话，可以转换成对数形式的相加。

等一下，这玩意怎么有点熟悉？：

\(20\log_{10}{M1}\)

这玩意不就是电压的dB表示形式吗？：

\(20\log_{10}{M1} = 20 \times \log_{10}\frac{U1}{U0}\)

那么上图中的放大器的表示形式可以变成：

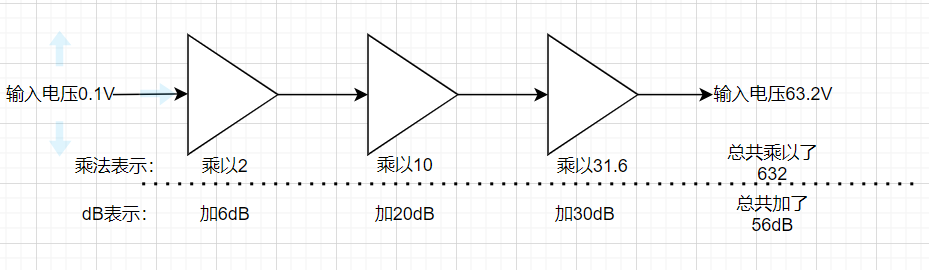
可以看到通过dB这个单位，我们把难搞的乘法变成了简单的加法。（想象不到吧表情）

可不可以使用绝对值？

上面说的那些都是相对值，如果我想用dB来表示一个绝对值的量，行不行？

当然可以，我们再把功率的dB公式拉出来一下：

\(L_{dB} = 10 \times \log_{10}\frac{P1}{P0}\)

我们发现只要P0设置成一个固定的值，然后把当前要计算的功率代入到P1，最终的得到的L就是一个绝对值啊。

包括dBm或者dBV，以及其他dB后面加个单位的的表示方法都是这个思路。除了dBFS稍微有点特殊，下文会讲到。

dBm全称为：decibel relative to one milliwatt，所以他的公式即为：

\(L_{dBm} = 10 \times \log_{10}\frac{P1}{1mW}\)

其中1mW即为1毫瓦，如果P1是1W(1瓦)的话，那么代入可得到30dBm。

那么同理，dBV全称为：decibel relative to one volt，所以他的公式即为：

\(L_{dBV} = 20 \times \log_{10}\frac{U1}{1V}\)

如果U1为2伏特的话，那么代入可得到6dBV。

dB的好处还有啥

首先我们先上两张图观察一下：

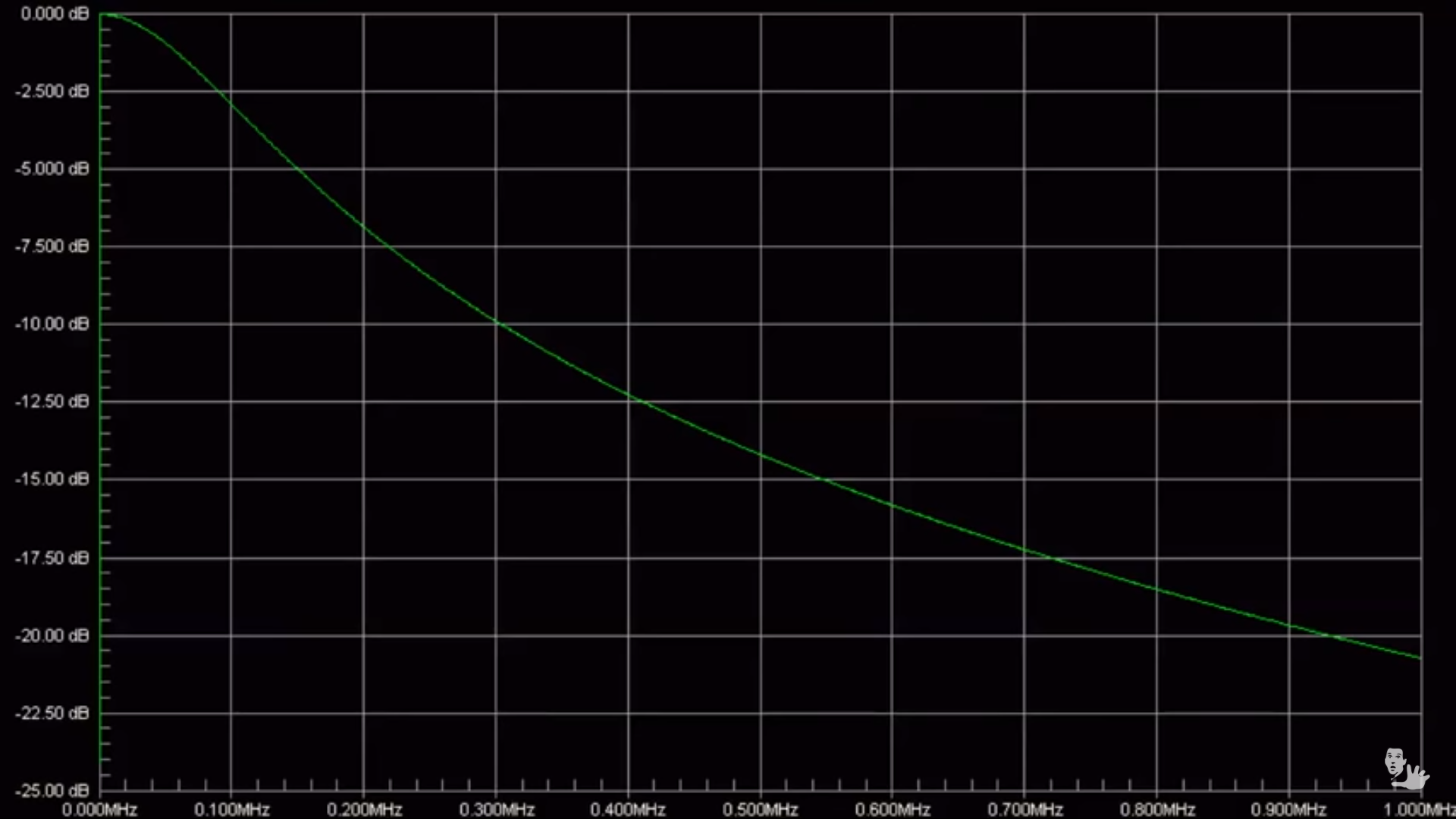
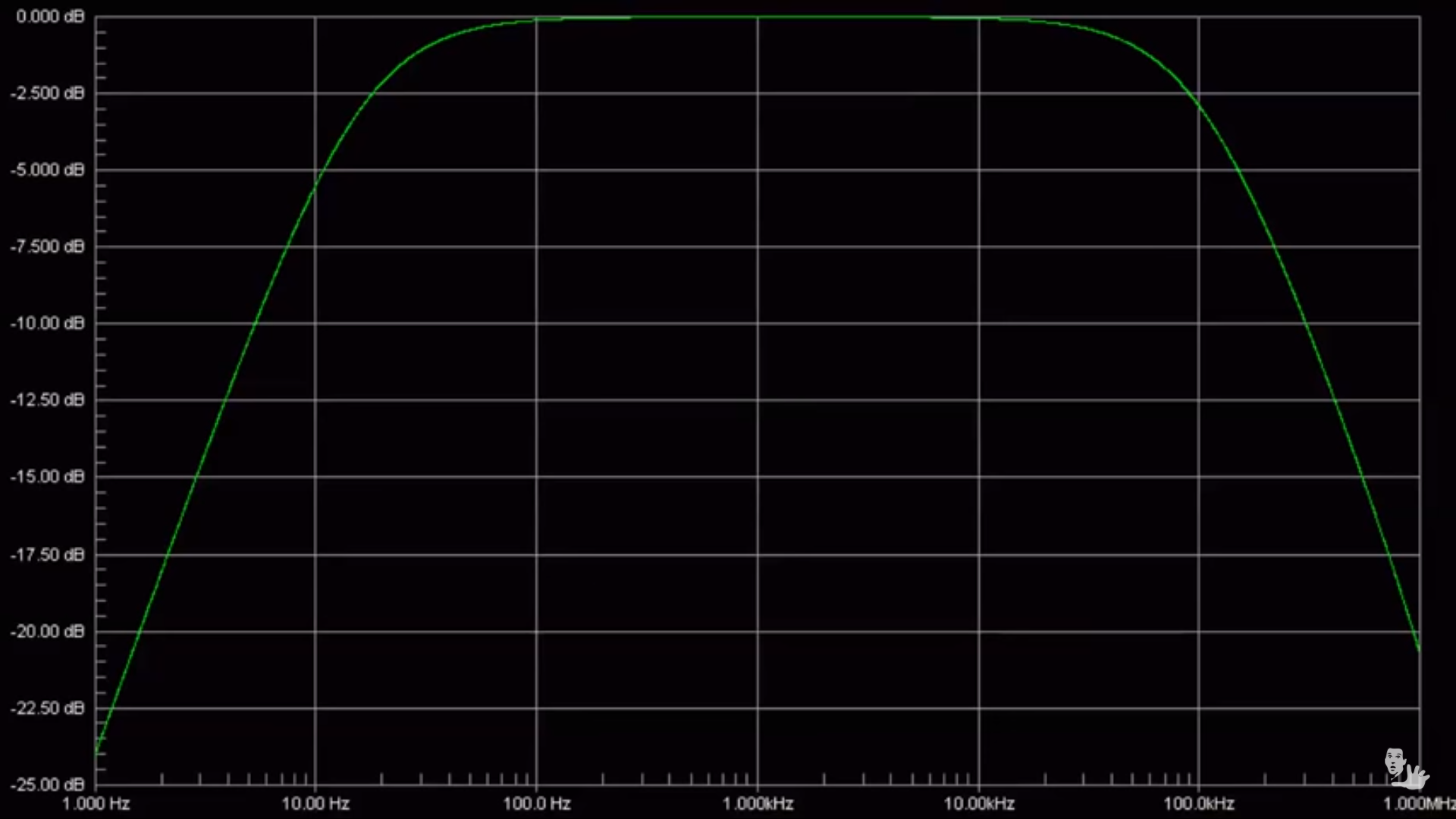
那么请耐心听我唠叨一下。这两张图描述的是同一个东西，只是使用了不同的单位。

其中纵坐标的单位是一样的，都是刚才说的dBV，比如0dBV就是1V，比如-6dBV就是0.5V。纵坐标代表了幅度，越往上幅度越大，没毛病。

横坐标就不一样了：

在前面这张图中0Hz到1MHz是线性递增的，因为这个区间范围太大了，所以无法看到0Hz到100Hz之间的具体信息，而只看到一条几乎贴近纵坐标的、陡峭上升的绿色斜线。

后面的这张图的横坐标”有点奇怪“，横坐标分别为1Hz、10Hz、100Hz、1kHz、10kHz、100kHz、1MHz，这是以10倍数递增的关系，这样的优点很明显，我们可以看到各频率范围的信号幅度。可以看到10Hz~100kHz的范围内的信号的幅度比较大，其他频率范围的幅度比较低。

这种10倍数递增的横坐标为什么能这么标，它的本质是什么？它的本质就是dB呀~

为了说明问题，那么在这里我们发明一个新的单位dBHz：

\(L_{dBHz} = 10 \times \log_{10}\frac{F1}{1Hz}\)

F1是频率，它的单位是Hz。那么分别把奇怪的横坐标：1Hz、10Hz、100Hz、1kHz、10kHz、100kHz、1MHz代入到上面这个公式可以得到：

0dBHz、10dBHz、20dBHz、30dBHz、40dBHz、50dBHz、60dBHz。可以看到这个横坐标在dBHz的角度看是“线性”增长的，妙啊，没毛病！

dBFS又妙在哪里

dBFS的全称是Decibels relative to full scale。dBFS和dBm之间有固定的转化关系：

\(X_{dBFS} = Y_{dBm} - MAXOUTPUT_{dBm}\)

但是不同设备的MAXOUTPUT即最大输出功率不一样，比如如果一个器件的最大输出功率是20dBm（也即100mW），那么：

\(X_{dBFS} = Y_{dBm} -20\)

所以在这个器件中，当我们想把dBm设置成最大的20dBm的时候，需要把dBFS设置成0。当想把dBm设置成5dBm的时候，需要把dBFS设置成-15。

所以dBFS的最大值就是0。为啥需要dBFS这个设定这么奇怪的单位？这是因为在数字域中我们需要设置信号的幅度。

小伙子，本老同志又要上公式了，你不能闪！

在16bit的信号中，幅度（AMP）和dBFS之间的关系如下：

\(L_{dBFS} = 10 \times \log_{10}(\frac{AMP}{INT16MAX})^{2}\)

也即：

\(L_{dBFS} = 20 \times \log_{10}\frac{AMP}{INT16MAX}\)

正因为这条公式的定义，才会有dBFS最大值为0的设定。因为AMP幅度最大是INT16MAX，计算出公式得到dBFS为0。

注：INT16MAX为16位有符号数的最大值，即为32767

一般在代码中会根据设置的dBFS的值然后计算得出当前的AMP幅度。

至于公式中为什么会有这个平方：

\((\frac{AMP}{INT16MAX})^{{\color{Red} 2}}\)

我是这么理解的，因为dBFS表示的依然是和dBm类似的功率的值，也即是最终以瓦特为单位。而器件中的电阻是固定的，幅度基本和电压一个单位，所以根据：

\(P = \frac{{U}^{2}}{R}\)

计算，最终幅度的确需要加一个平方。

因为本人水平有限，难免会有些纰漏或者没讲清楚的地方。可以加我公众号binfun或者留言讨论，谢谢！

感谢阅读！

巨人的肩膀：

https://www.youtube.com/watch?v=mLMfUi2yVu8