hdu3713 Double Maze

Problem Description

Unlike single maze, double maze requires a common sequence of commands to solve both mazes. See the figure below for a quick understanding.

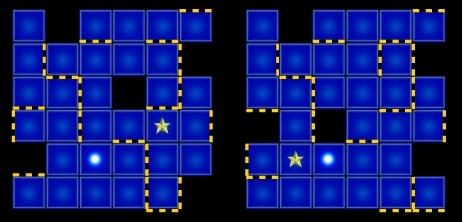
A maze is made up of 6*6 cells. A cell can be either a hole or a square. Moreover, a cell may be surrounded by barriers. There is ONLY one start cell (with a ball) and ONLY one end cell (with a star) in a single maze.These two cells are both squares. It is possible that the start cell and the end cell are the same one. The goal of a single maze is to move the ball from the start cell to the end cell. There are four commands in total,'L', 'D', 'R' and 'U' corresponding to moving the ball left, down, right and up one cell, respectively. The barriers may make the commands take no effect, i.e., the ball does NOT move if there is a barrier on the way.
When the ball gets to a hole or outside of the maze, it fails. A double maze is made up of two single mazes. The commands control two balls simultaneously, and the movements of two balls are according to the rules described above independently. Both balls will continue to move simultaneously if at least one of the balls has not got to the end cell.
So, a ball may move out of the end cell since the other ball has not been to the target. A double maze passes when both balls get to their end cells, or fails if either of the two mazes fails. The goal of double maze is to get the shortest sequence of commands to pass. If there are multiple solutions, get the lexical minimum one.
To simplify the input, a cell is encoded to an integer as follows. The lowest 4 bits signal the existence of the barriers around a cell. The fifth bit indicates whether a cell is a hole or not. The sixth and seventh bits are set for the start cell and end cell. Details are listed in the following table with bits counted from lowest bit. For a barrier, both of the two adjacent cells will have the corresponding barrier bit set. Note that the first two mazes in the sample input is the encoding of two mazes in the figure above, make sure you understand the encoding right.

 

Input

The first line of input gives the total number of mazes, T (1 < T ≤ 20). Then follow T mazes. Each maze is a 6*6 matrix, representing the encoding of the original maze. There is a blank line between mazes.

 

Output

For every two consecutive mazes, you should treat them as a double maze and output the answer. So there are actually T - 1 answers. For each double maze, output the shortest sequence of commands to pass. If there are multiple solutions, output the lexicographically minimum one. If there is no way to pass, output -1 instead.

 

Sample Input

3
16 0 18 16 18 24
20 19 24 16 28 1
18 28 17 0 22 17
25 20 17 18 88 20
2 16 48 28 17 16
24 16 16 20 23 1

16 0 18 16 18 24
20 19 24 20 29 1
18 28 17 16 22 17
8 20 1 18 24 20
19 80 48 24 16 0
24 16 16 16 22 19

18 16 18 16 18 80
24 18 24 16 24 18
18 24 0 0 18 24
24 18 0 0 24 18
18 24 18 16 18 24
56 18 24 18 24 18

 

Sample Output

RRLULLLRRDLU
RURDRLLLURDULURRRRRDDU

 

Author

GAO, Yuan

 

Source

2010 Asia Chengdu Regional Contest

 

Recommend

zhengfeng

题意：给出两个迷宫，每个迷宫各有起点和终点，有的格子能走有的不行，格子与格子之间还可能有护栏。同时控制两个迷宫每次朝同一个方向移动，问最快使得两个迷宫同时到达终点的步数，有多个最优解输出字典序最小的一个。

思路：把两个图合成一个图，建边，用bfs，总共也就6的4次方个点。以dlru的顺序查找，找到的保证字典序最小。用一个数组记录其前驱点，找到答案后倒着输出就好。

#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;

#define two(x) (1<<x)
#define inf 200000000
int  T;
char c[4]={'D','L','R','U'};
int d[2][37][4],st[2],en[2],f[37][37];
bool can[2][37];
int fa1[37][37],fa2[37][37],dir[37][37],ans[2000];

void init(int cur)
{
	memset(d[cur],0,sizeof(d[cur]));
	memset(can[cur],1,sizeof(can[cur]));
	int x;
	for (int i=1;i<=6;++i)
		for (int j=1;j<=6;++j)
		{
			int t=(i-1)*6+j;
			scanf("%d",&x);
			if (x & two(1)) d[cur][t][0]=t;
			else if (i<6) d[cur][t][0]=t+6;
			if (x & two(0)) d[cur][t][1]=t;
			else if (j>1) d[cur][t][1]=t-1;
			if (x & two(2)) d[cur][t][2]=t;
			else if (j<6) d[cur][t][2]=t+1;
			if (x & two(3)) d[cur][t][3]=t;
			else if (i>1) d[cur][t][3]=t-6;
			if ((x & two(4))==0) can[cur][t]=false;
			if (x & two(5)) st[cur]=t;
			if (x & two(6)) en[cur]=t;
		}
}

void bfs()
{
	queue<int> q1,q2;
	bool p[37][37];
	memset(p,1,sizeof(p));
	q1.push(st[0]);
	q2.push(st[1]);
	p[st[0]][st[1]]=false;
	while (!q1.empty())
	{
		int x=q1.front(),y=q2.front();
		q1.pop();q2.pop();
		for (int i=0;i<=3;++i)
		{
			int tx=d[0][x][i],ty=d[1][y][i];
			if (tx && ty && can[0][tx] && can[1][ty])
				if (p[tx][ty])
				{
					q1.push(tx);
					q2.push(ty);
					p[tx][ty]=false;
					fa1[tx][ty]=x;
					fa2[tx][ty]=y;
					dir[tx][ty]=i;
				}
		}
	}
}

void solve()
{
	memset(dir,-1,sizeof(dir));
	dir[st[0]][st[1]]=5;
	bfs();
	int x=en[0],y=en[1];
	if (dir[x][y]==-1)
	{
		printf("-1\n");
		return;
	}
	int tot=0,tx,ty;
	while (!(x==st[0] && y==st[1]))
	{
		ans[++tot]=dir[x][y];
		tx=fa1[x][y];
		ty=fa2[x][y];
		x=tx;y=ty;
	}
	for (int i=tot;i>0;--i)
		printf("%c",c[ans[i]]);
	printf("\n");
}

int main()
{
	scanf("%d",&T);
	init(1);
	for (int i=2;i<=T;++i)
	{
		init(1 & i);
		solve();
	}
	return 0;
}