Kosaraju算法详解

• Kosaraju算法是干什么的？

Kosaraju算法可以计算出一个有向图的强连通分量

• 什么是强连通分量？

在一个有向图中如果两个结点（结点v与结点w）在同一个环中（等价于v可通过有向路径到达w，w也可以到达v）它们两

个就是强连通的，所有互为强连通的点组成了一个集合，在一幅有向图中这种集合的数量就是这幅图的强连通分量的数量

• 怎么算？？

第一步：计算出有向图 (G) 的反向图 (G反) 的逆后序排列（代码中有介绍）

第二步：在有向图 (G) 中进行标准的深度优先搜索，按照刚才计算出的逆后序排列顺序而非标准顺序，每次搜索访问的所有点即在同一强连通分量中

 class Kosaraju {
     private Digraph G;
     private Digraph reverseG; //反向图
     private Stack<Integer> reversePost; //逆后续排列保存在这
     private boolean[] marked;
     private int[] id; //第v个点在几个强连通分量中
     private int count; //强连通分量的数量
     public Kosaraju(Digraph G) {
         int temp;
         this.G = G;
         reverseG = G.reverse();
         marked      = new boolean[G.V()];
         id          = new int[G.V()];
         reversePost = new Stack<Integer>();

         makeReverPost(); //算出逆后续排列

         for (int i = 0; i < marked.length; i++) { //重置标记
             marked[i] = false;
         }

         for (int i = 0; i < G.V(); i++) { //算出强连通分量
             temp = reversePost.pop();
             if (!marked[temp]) {
                 count++;
                 dfs(temp);
             }
         }
     }
     /*
      * 下面两个函数是为了算出 逆后序排列
      */
     private void makeReverPost() {
         for (int i = 0; i < G.V(); i++) { //V()返回的是图G的节点数
             if (!marked[i])
                 redfs(i);
         }
     }

     private void redfs(int v) {
         marked[v] = true;
         for (Integer w: reverseG.adj(v)) { //adj(v)返回的是v指向的结点的集合
             if (!marked[w])
                 redfs(w);
         }
         reversePost.push(v); //在这里把v加入栈,完了到时候再弹出来,弹出来的就是逆后续排列
     }
     /*
      * 标准的深度优先搜索
      */
     private void dfs(int v) {
         marked[v] = true;
         id[v] = count;
         for (Integer w: G.adj(v)) {
             if (!marked[w])
                 dfs(w);
         }
     }

     public int count() { return count;}
 }

• 为什么这样就可以算出强连通分量的数量？（稍微有些费解）

比如有这样一个图，它有五个强连通分量

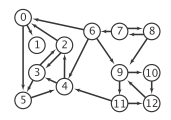
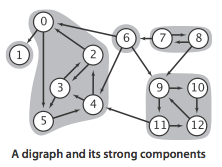
我们需要证明在26行的dfs(temp)中找到的①全是点temp的强连通点，②且是它全部的强连通点

证明时不要忘了定义：v可通过有向路径到达w，w也可以到达v，则它俩强连通

先证明②：

用反证法，就假如对一个点（点w）深度优先搜索时有一个它的强连通点（点v）没找到。

如果没找到，那就说明 点v 已经在找其他点时标记过了，

但 点v 如果已经被标记过了，因为有一条 v  -> w 的有向路径，那 点w 肯定也被找过了，

那就不会对 点w 深度优先搜索了。

假设不成立     (*^ω^*)

再证明①：

对一个点（点w）深度优先搜索时找到了一个点（点v），说明有一条 w -> v 的有向路径，再证明有一条 v -> w 的路径就行了，

　　　　　证明有一条 v -> w 的路径，就相当于证明图G的反向图（G反）有一条 w -> v 的有向路径，

　　　　　因为 点w 和 点v 满足那个 逆后序排列，而逆后序排列是在redfs(node)结束时将node加入栈，再从栈中弹出，

　　　　　那说明反向图的深度优先搜索中redfs(v)肯定在redfs(w)前就结束了，

　　　　　那就是两种情况：

　　　　　■ redfs(v)已经完了redfs(w)才开始

　　　　　■ redfs(v)是在 redfs(w)开始之后结束之前 结束的，也就是redfs(v)是在redfs(w)内部结束的

　　　　   第一种情况不可能，因为 G反 有一条 v -> w 的路径（因为G有一条 w -> v 的路径），

　　　　　满足第二中情况即在 G反 中有一条 w -> v 的路径。

　　　　　终于证完了。。。。。。

完整代码：

 package practice;

 import java.util.ArrayList;
 import java.util.Stack;

 public class TestMain {
     public static void main(String[] args) {
         Digraph a = new Digraph(13);
         a.addEdge(0, 1);a.addEdge(0, 5);a.addEdge(2, 3);a.addEdge(2, 0);a.addEdge(3, 2);
         a.addEdge(3, 5);a.addEdge(4, 3);a.addEdge(4, 2);a.addEdge(5, 4);a.addEdge(6, 0);
         a.addEdge(6, 4);a.addEdge(6, 9);a.addEdge(7, 6);a.addEdge(7, 8);a.addEdge(8, 7);
         a.addEdge(8, 9);a.addEdge(9, 10);a.addEdge(9, 11);a.addEdge(10, 12);a.addEdge(11, 4);
         a.addEdge(11, 12);a.addEdge(12, 9);

         Kosaraju b = new Kosaraju(a);
         System.out.println(b.count());
     }
 }

 class Kosaraju {
     private Digraph G;
     private Digraph reverseG; //反向图
     private Stack<Integer> reversePost; //逆后续排列保存在这
     private boolean[] marked;
     private int[] id; //第v个点在几个强连通分量中
     private int count; //强连通分量的数量
     public Kosaraju(Digraph G) {
         int temp;
         this.G = G;
         reverseG = G.reverse();
         marked      = new boolean[G.V()];
         id          = new int[G.V()];
         reversePost = new Stack<Integer>();

         makeReverPost(); //算出逆后续排列

         for (int i = 0; i < marked.length; i++) { //重置标记
             marked[i] = false;
         }

         for (int i = 0; i < G.V(); i++) { //算出强连通分量
             temp = reversePost.pop();
             if (!marked[temp]) {
                 count++;
                 dfs(temp);
             }
         }
     }
     /*
      * 下面两个函数是为了算出 逆后序排列
      */
     private void makeReverPost() {
         for (int i = 0; i < G.V(); i++) { //V()返回的是图G的节点数
             if (!marked[i])
                 redfs(i);
         }
     }

     private void redfs(int v) {
         marked[v] = true;
         for (Integer w: reverseG.adj(v)) { //adj(v)返回的是v指向的结点的集合
             if (!marked[w])
                 redfs(w);
         }
         reversePost.push(v); //在这里把v加入栈,完了到时候再弹出来,弹出来的就是逆后续排列
     }
     /*
      * 标准的深度优先搜索
      */
     private void dfs(int v) {
         marked[v] = true;
         id[v] = count;
         for (Integer w: G.adj(v)) {
             if (!marked[w])
                 dfs(w);
         }
     }

     public int count() { return count;}
 }
 /*
  * 图
  */
 class Digraph {
     private ArrayList<Integer>[] node;
     private int v;
     public Digraph(int v) {
         node = (ArrayList<Integer>[]) new ArrayList[v];
         for (int i = 0; i < v; i++)
             node[i] = new ArrayList<Integer>();
         this.v = v;
     }

     public void addEdge(int v, int w) { node[v].add(w);}

     public Iterable<Integer> adj(int v) { return node[v];}

     public Digraph reverse() {
         Digraph result = new Digraph(v);
         for (int i = 0; i < v; i++) {
             for (Integer w : adj(i))
                 result.addEdge(w, i);
         }
         return result;
     }

     public int V() { return v;}

 }