[Bayesian] “我是bayesian我怕谁”系列 - Continuous Latent Variables

打开prml and mlapp发现这部分目录编排有点小不同，但神奇的是章节序号竟然都为“十二”。

prml：pca --> ppca --> fa

mlapp：fa --> pca --> ppca

这背后又有怎样的隐情？不可告人的秘密又会隐藏多久？

基于先来后到原则，走prml路线。

首先，这部分内容，尤其是pca，都是老掉牙且稳定的技术，既然是统计机器学习，这次的目的就是借概率图来缕一遍思路，以及模型间的内在联系。

我们要建立的是一套完整的知识体系，而非“拿来一用，用完就扔”的态度。

有菜鸡问了，为何你总是强调“体系”？

因为我是马刺队球迷。

首先，我希望大家重视prml的第12章开章这段话：

"本章中，我们⾸先介绍标准的、⾮概率的PCA⽅法，然后我们会说明，当求解线性⾼斯潜在变量模型的⼀种特别形式的最⼤似然解时， PCA如何⾃然地产⽣。这种概率形式的表⽰⽅法会带来很多好处，例如在参数估计时可以使⽤EM算法，对混合PCA模型的推广以及主成分的数量可以从数据中⾃动确定的贝叶斯公式。最后，我们简短地讨论潜在变量概念的几个推广，使得潜在变量的概念不局限于线性⾼斯假设。这种推广包括⾮⾼斯潜在变量，它引出了独⽴成分分析（ independent conponent analysis）的框架。这种推广还包括潜在变量与观测变量的关系是⾮线性关系的模型。"

因为大部分人都只关心以下这张图，也就是通过“映射”的角度来理解PCA。

然后，因为理解不全面，或者暂且只关心pca，对后面的部分就出现了理解断层。因为体系，波波维奇劝你要“站得高，看得远”。

---

PCA:

有关pca的内容，网络资源有太多，以下个人链接能增加一点感性认识和相关内容；至于理性认识，除了动手亲自推倒公式，哪怕是抄一遍，也是极好的。

• [Scikit-learn] 4.4 Dimensionality reduction - PCA
• [Scikit-learn] 1.2 Dimensionality reduction - Linear and Quadratic Discriminant Analysis

因为pca+gmm常常是一个组合，先降维，去掉可能useless的信息，再进行gmm聚类。如此，至少能节省后期聚类时的计算资源。

其他没什么想说的，这个组合实践时确实效果蛮好，PCA也算是重要的预处理工具，数据预处理的地位你懂得，特征工程之百试不爽。

PPCA:

冒出一个“屁＋PCA”，恩，本来就挺好用，还要加个“P”？ —— 初次见面的初次感受。

PCA也可以被视为概率潜在变量模型的最⼤似然解。如何理解？

From: http://www.miketipping.com/papers/met-mppca.pdf【链接中x是隐变量】

第一步：

先验：

似然：【原理见证明1，t = Wx+mu】

后验：

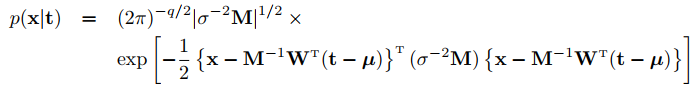
最后，期望就是最优解。贝叶斯三部曲，没啥可说的，但这里有个Ｍ，如果假设σ²  = 0, 再带入结果，这不就是PCA麽。

第二步：

解的形式有了，但解中的变量是多少，比如W应该是多少呢？

通过mle获取，也就是获得Ｗ的估值。

(1)

联合分布，再积分掉x得t的边缘分布：

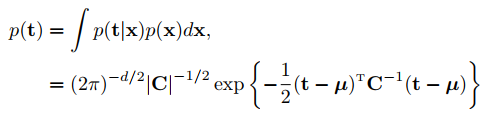
(2)

然后便获取了"t的似然"形式，如下：

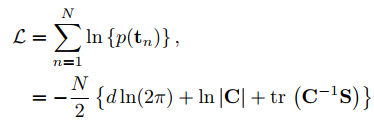
求导解似然方程就不再赘述here，过程详见链接。

答案中就包含了W的估值。读后感就是：一切皆是套路。

证明1

假设z是标准高斯，那么线性组合的每个x也是高斯。

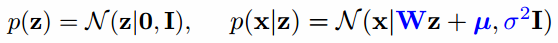
Figure, 证明１

这个证明看似很无聊，让我们思维大胆地扩展一下：

线性组合类似于没激活神经元的神经网络（NN）；因为有了激活函数，nn才能解决非线性问题。

但这里对应的貌似不是激活函数，而是概率。概率能否达到非线性的效果？为什么？

与传统的PCA相⽐，会带来一个本人感兴趣的优势就是，可以利用em高效求解。

好比用几何和代数解决同一个问题：用em总比“求解特征向量特征值”要划算的多，而且结果等价。当然还有其他优势，例如处理missing data。

此时，两个问题可能在菜鸡小脑中回荡：

• 不要问我mle方法中怎么涉及到了特征值计算，自己写一下Ｗ的估值瞧瞧。
• 感觉似乎都搞完了啊，但怎么又涉及到了em？

读到这里，你如果有同样的疑惑，恭喜。好处便是，你不会感觉这系列文章的思维读来怪异，因为你我的脑回路可能是相通的。

因为mle在高维计算时没啥优势，所以考虑em。

这里看似是放弃了由mle得到的精确值，转而选择em带来的估计值，建议你想想，能提高内力心法。

因为FA就是ppca的方差扩展版本，所以，em的方法在fa中聊一次就好，节能。

FA:

cs229

既然是ppca的扩展，那么，咱就看看扩展ppca会发生什么？

首先，凭什么ppca的“先验”是标准高斯？改一改会如何？

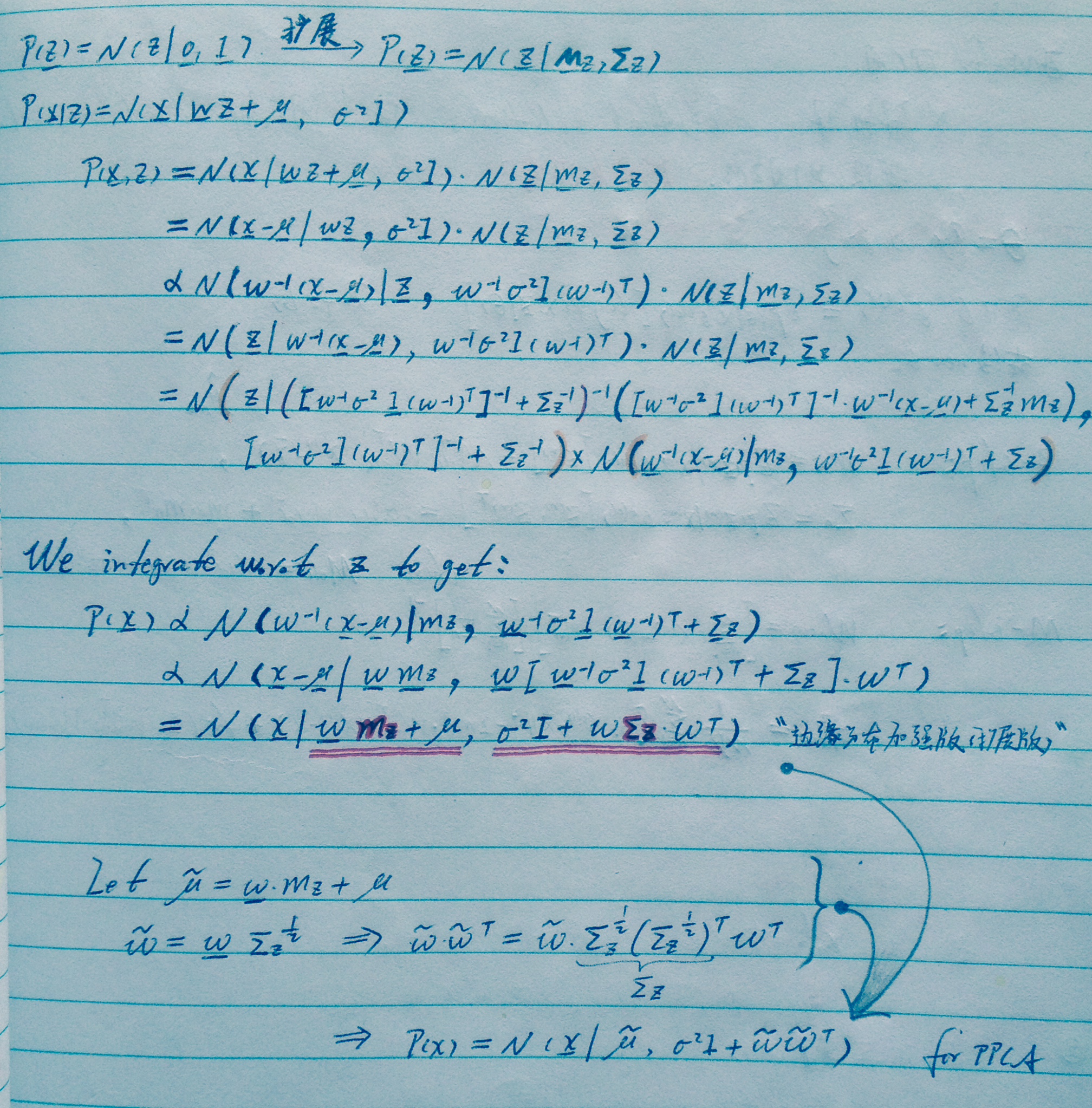
结论：x的边缘分布可以变为原来熟悉的样子。

按照fa的思路，凭什么x的边缘分布的方差是标准化的东东，改改会如何？

 

结论：还是这个熟悉的形式。

可见，“龙生龙，凤生凤，老鼠的儿子会打洞”，高斯的衍生还是那么“高斯”。

但问题是：边缘分布有点复杂，所以用em。

链接中用的Λ表示Ｗ，其他符号一致。

E step:

既然是em，E步骤计算：p(z⁽ⁱ⁾ | x⁽ⁱ⁾ ; µ, Λ, Ψ)

这里技巧在于，z和x都是高斯，一并构成了一个联合变量p(z, x)，这个东西通过p(z) * p(x|z)就可以求得。

那么P(z|x)就可以通过以下公式直接求得：

调整一下思维：

p(z), p(x|z), p(x)都有，本可以通过贝叶斯公式计算，但几个这么复杂的高斯除来除去，是个什么鬼？感觉也不好计算。

所以，先人给出了以上公式，通过联合概率就直接写出结果了。

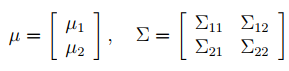
注意，联合概率是个高维高斯，且有两部分，一部分也可能包含多个维度。

Ｍ step:

思路就是通过log{P(x)}对各个参数求导。具体步骤，详见cs229链接，有超详细步骤，不再赘述。

先写到这里，本文只记录学习思路，帮助你建立知识体系，不会也不可能取代任何教材。

这一领域的东西，要充分领会，只能亲自动手算上一算。有时，你可能卡在一处无法进一步理解，该文可能会起到一点点“雪中送炭”的作用，这就足够了。

最后，再看：

prml：pca --> ppca --> fa

mlapp：fa --> pca --> ppca

如写小说，一个循序渐进，一个倒叙法。