Fibonacci Check-up
Fibonacci Check-up |
| Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) |
| Total Submission(s): 42 Accepted Submission(s): 27 |
|
Problem Description
Every ALPC has his own alpc-number just like alpc12, alpc55, alpc62 etc.
As more and more fresh man join us. How to number them? And how to avoid their alpc-number conflicted? Of course, we can number them one by one, but that’s too bored! So ALPCs use another method called Fibonacci Check-up in spite of collision. First you should multiply all digit of your studying number to get a number n (maybe huge). |
|
Input
First line is the testcase T.
Following T lines, each line is two integers n, m ( 0<= n <= 10^9, 1 <= m <= 30000 ) |
|
Output
Output the alpc-number.
|
|
Sample Input
2 |
|
Sample Output
1 |
|
Source
2009 Multi-University Training Contest 5 - Host by NUDT
|
|
Recommend
gaojie
|
/*
题意:给出你公式,让你求( 求和C(k,n)F(k) )%m 初步思路:没思路,先打表
得到:
0
1
3
8
21
55
144
377
987
2584
6765
17711
46368
121393
317811
832040
2178309
5702887
14930352
39088169
102334155
能得出来,G(0)=0;
G(1)=1;
G(n)=3*G(n-1)-G(n-2);
然后用矩阵快速幂求出结果 最重要的构造矩阵还没学线性代数的我只能试着推出来:
|G(n) G(n-1)| | 3 1 |
| 0 0 |*| -1 0 | #总结:板没调好,WA了两发 */
#include<bits/stdc++.h>
using namespace std;
int n,mod;
int t;
/********************************矩阵模板**********************************/
class Matrix {
public:
int a[][];
int n; void init(int x) {
memset(a,,sizeof(a));
if(x){
a[][]=;
a[][]=;
a[][]=-;
a[][]=;
}else{
a[][]=;
a[][]=;
a[][]=;
a[][]=;
}
n=;
} Matrix operator +(Matrix b) {
Matrix c;
c.n = n;
for (int i = ; i < n; i++)
for (int j = ; j < n; j++)
c.a[i][j] = (a[i][j] + b.a[i][j]) % mod;
return c;
} Matrix operator +(int x) {
Matrix c = *this;
for (int i = ; i < n; i++)
c.a[i][i] += x;
return c;
} Matrix operator *(Matrix b)
{
Matrix p;
p.n = b.n;
memset(p.a,,sizeof p.a);
for (int i = ; i < n; i++)
for (int j = ; j < n; j++)
for (int k = ; k < n; k++)
p.a[i][j] = (p.a[i][j] + (a[i][k]*b.a[k][j])%mod) % mod;
return p;
} Matrix power_1(int t) {
Matrix ans,p = *this;
ans = p;
while (t) {
if (t & )
ans=ans*p;
p = p*p;
t >>= ;
}
return ans;
} Matrix power_2(Matrix a,Matrix b,int x){
while(x){
if(x&){
b=a*b;
}
a=a*a;
x>>=;
}
return b;
}
};
/********************************矩阵模板**********************************/
Matrix unit,init;
int main(){
// freopen("in.txt","r",stdin);
scanf("%d",&t);
while(t--){
scanf("%d%d",&n,&mod);
unit.init();//存放G(n)的矩阵
init.init();//子矩阵
if(n==){
printf("0\n");
continue;
}else if(n==){
printf("%d\n",%mod);
continue;
}
init=init.power_1(n-);
unit=unit*init;
// cout<<mod<<endl;
// for(int i=0;i<2;i++){
// for(int j=0;j<2;j++){
// cout<<init.a[i][j]<<" ";
// }
// cout<<endl;
// } printf("%d\n",(unit.a[][]+mod)%mod);
}
return ;
}
/*
附上打表小程序
*/
#include<bits/stdc++.h>
using namespace std;
long long Sums(long long n,long long k) //函数定义
{
long long sum = ,N=,K=,M=;
if(k > && k<=n)
{
for(long long i = ;i<=n;i++)
{
N = N * i;
} for(long long j = ;j <= k;j++)
{
K = K * j;
} for(long long h = ;h <= n-k;h++)
{
M = M * h;
}
sum=N/(K*M);
return sum;
}
else
return ;
}
int main(){
//freopen("in.txt","r",stdin);
long long f[];
f[]=;
f[]=;
for(long long i=;i<=;i++)
f[i]=f[i-]+f[i-];
for(long long n=;n<=;n++){
long long cur=;
for(long long k=;k<=n;k++){
long long cnk=Sums(n,k);
//cout<<"C("<<k<<","<<n<<")="<<cnk<<endl;
cur+=cnk*f[k];
}
cout<<cur<<endl;
}
return ;
}
Fibonacci Check-up的更多相关文章
- 可变长度的Fibonacci数列
原题目: Write a recursive program that extends the range of the Fibonacci sequence. The Fibonacci sequ ...
- Applying Eigenvalues to the Fibonacci Problem
http://scottsievert.github.io/blog/2015/01/31/the-mysterious-eigenvalue/ The Fibonacci problem is a ...
- hdu 5167 Fibonacci 打表
Fibonacci Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others) Proble ...
- 【Fibonacci】BestCoder #28B Fibonacci
Fibonacci Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)Total S ...
- hdu 5167 Fibonacci(预处理)
Problem Description Following is the recursive definition of Fibonacci sequence: Fi=⎧⎩⎨01Fi−1+Fi−2i ...
- [Algorithm] Fibonacci Sequence - Anatomy of recursion and space complexity analysis
For Fibonacci Sequence, the space complexity should be the O(logN), which is the height of tree. Che ...
- fibonacci数列的性质和实现方法
fibonacci数列的性质和实现方法 1.gcd(fib(n),fib(m))=fib(gcd(n,m)) 证明:可以通过反证法先证fibonacci数列的任意相邻两项一定互素,然后可证n>m ...
- LeetCode 842. Split Array into Fibonacci Sequence
原题链接在这里:https://leetcode.com/problems/split-array-into-fibonacci-sequence/ 题目: Given a string S of d ...
- LeetCode 873. Length of Longest Fibonacci Subsequence
原题链接在这里:https://leetcode.com/problems/length-of-longest-fibonacci-subsequence/ 题目: A sequence X_1, X ...
- 算法与数据结构(九) 查找表的顺序查找、折半查找、插值查找以及Fibonacci查找
今天这篇博客就聊聊几种常见的查找算法,当然本篇博客只是涉及了部分查找算法,接下来的几篇博客中都将会介绍关于查找的相关内容.本篇博客主要介绍查找表的顺序查找.折半查找.插值查找以及Fibonacci查找 ...
随机推荐
- xml跟sql查找
xml小白笔记 ....... <sql id="wDishesColumns"> a.id AS "id", a.pid AS "pid ...
- http://codeforces.com/problemset/problem/545/D
D. Queue time limit per test 1 second memory limit per test 256 megabytes input standard input outpu ...
- Linux视频主要概述
Linux当中称之为视频的主要为俩个方面(主要以kernel为主): 1.源代码video目录指的是主显示输出,也就是帧缓冲(Frame Buffer)驱动部分,表示对基本图形层的显示支持; 2.源代 ...
- Java历程-初学篇 Day02变量,数据类型和运算符
一,数据类型 1,基础数据类型 整型 byte short int long 浮点型 float double 字符型 char 布尔类型 boolean 2,引用类型 String 字符串型 二,变 ...
- 用shell脚本新建shell文件并自动生成头说明信息
目标: 新建文件后,直接给文件写入下图信息 代码实现: [root@localhost test]# vi AutoHead.sh #!/bin/bash#此程序的功能是新建shell文件并自动生成头 ...
- Nunit测试工具使用实例
前言: 本文主要是介绍了Nunit的基本使用,其中参详了很多已有的文章,由于最近要使用其进行测试,所以对网上的文章做了下整理,同时加入了一些自己的实践. NUnit的属性 TestFixture 它标 ...
- ASP.NET没有魔法——ASP.NET MVC 与数据库之MySQL
之前介绍了My Blog如何使用ADO.NET来访问SQL Server获取数据.本章将介绍如何使用My SQL来完成数据管理. 在使用My SQL之前需确保开发环境中安装了My SQL数据库和Con ...
- web自动化测试从入门到持续集成(selenium webdriver)
在很多刚学习自动化的可能会认为我只需要会运用selenium,我只需要在一个编辑器中实用selenium +java编写了一些脚本那么就会自动化了,是真的吗?答案肯定是假的.自动化肯定是需要做到真的完 ...
- PHP 支付
蚂蚁金服开放平台 2.下载PHP的SDK&demo 3.申请应用 OR 使用沙箱环境 4.生成应用私钥&应用公钥 5.配置config.php 蚂蚁金服开放平台",对,没错, ...
- wpf GifBitmapDecoder 解析 gif 格式
在网上有很多图片都是gif,那么如何在 wpf 解析 gif? 本文告诉大家如何使用 GifBitmapDecoder 把gif分开为一张一张,获得他的信息. 如果需要把一个 gif 分开,使用的代码 ...

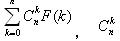 , is the combination number. The answer mod m (the total number of alpc team members) is just your alpc-number.
, is the combination number. The answer mod m (the total number of alpc team members) is just your alpc-number.