逻辑回归，附tensorflow实现

本文旨在通过二元分类问题、多元分类问题介绍逻辑回归算法，并实现一个简单的数字分类程序

在生活中，我们经常会碰到这样的问题：

根据苹果表皮颜色判断是青苹果还是红苹果

根据体温判断是否发烧

这种答案只有两种可能的问题(y {0,1})，被称为二元分类问题

有一组数据：

(x,y) {(1,0), (2,0), (3,0), (4,0), (5,0),

(6,1), (7,1), (8,1), (9,1), (10,1) }

这组数据在二维平面表现如下：

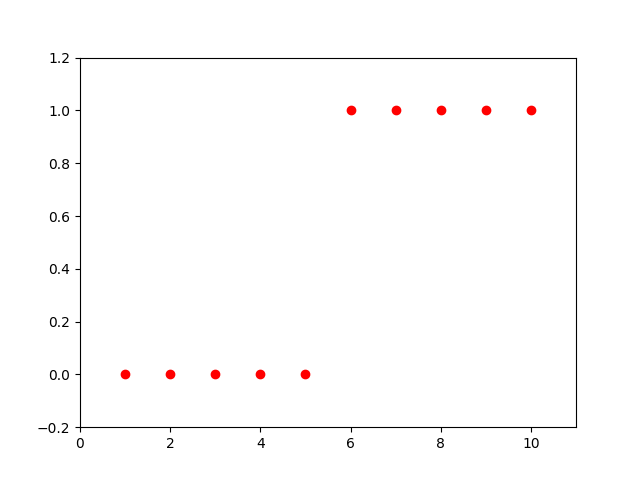
现在要根据x的值把这些点分成2类

我们先按照线性回归的思路来拟合出一条直线，如下图

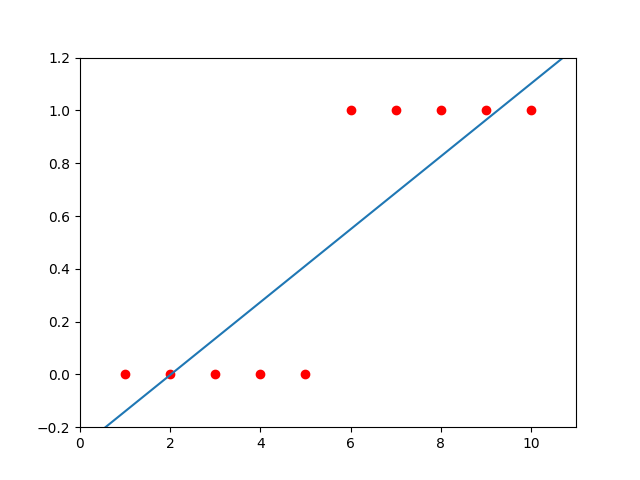
由于是二元分类问题，我们判断当h(x)>0.5时，y=1；当h(x)<0.5时，y=0；画出来差不多是这么个样子

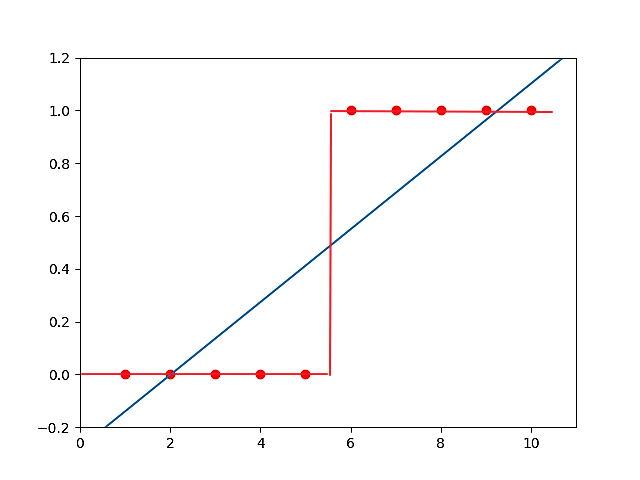
到现在为止看起来线性回归干得不错，但是当我们在数据中加一个噪声点(15,1)的时候：

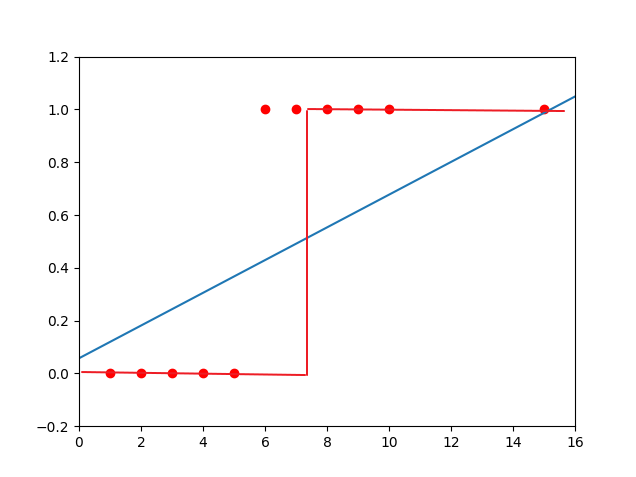
可以看到，(6,1)(7,1)两个点都没有被正确的拟合

为了解决此问题，引入sigmoid函数

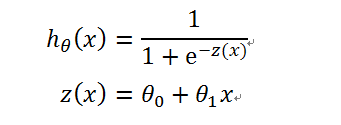
函数图是一个漂亮的S形

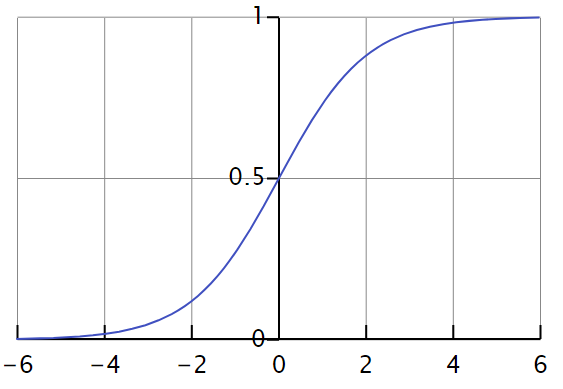图片来自wiki

可以看出，当z(x)>0的时候，h(x)>0.5，由此判断y=1；反之则判断y=0

不过在实际使用中，更多的把h(x)看做是y=1的概率，1-h(x)看做是y=0的概率

例如h(x)=0.5，意味着y=1的概率为50%

由此把二元分类问题转化成了概率问题

那么怎么判断我们预测的是否准确，换句话说该怎样定义cost function呢

引入交叉熵

交叉熵产生于信息论里面的信息压缩编码技术，但是它后来演变成为从博弈论到机器学习等其他领域里的重要技术手段；公式如下

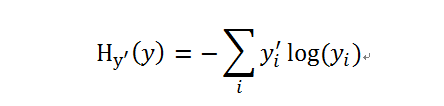
其中 y是预测的值， 是实际的值；比较粗糙的理解是，交叉熵是用来衡量我们的预测用于描述真相的有效性；更详细的证明在此不进一步展开

PS：一般在二元分类问题中都介绍最大似然法；在分类问题中交叉熵本质上与最大似然法相同，故在此只介绍交叉熵

在此稍微说明一下交叉熵为何有效

先让我们看一下-log(x)在0-1区间的函数图像：

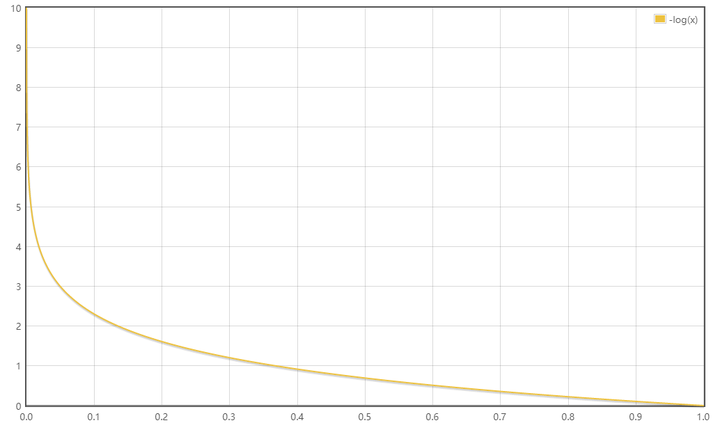
假设 =1，y=0.6，转换成向量表达为 =[0,1]， =[0.4,0.6]

此时

假设 =1，y=0.99，转换成向量表达为 =[0,1]， =[0.01,0.99]

此时

假设 =1，y=0.01，转换成向量表达为 =[0,1]， =[0.99,0.01]

此时

可以看出，当我们预测得越准确时，cost function的值就越小；当预测错误时，cost function就会很大

所以问题就又来到了之前讨论过的的最小化cost function上

在上面的二元分类问题中，问题的答案只有是和否(y {0,1})；但是很多问题的答案并不那么简单，比如说：

手写一个数字，识别改数字的值(y {0,1,2,3,4,5,6,7,8,9} )

根据一个汽车的标识，识别汽车的生产厂商(y { 奔驰，宝马，奥迪等等 })

这类问题被称为多元分类问题

很明显，sigmoid函数并不能满足多元分类问题的需要

在此引入softmax函数，函数如下

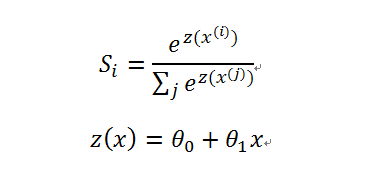
关于softmax的运作机制，可以参考下图

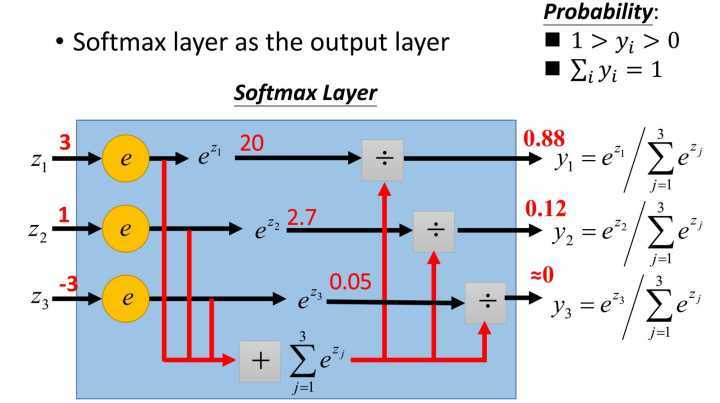图片来自《一天搞懂深度学习》

cost function还是使用前文提到的交叉熵即可

那么一个简单的数字识别算法实现如下：

关于这段代码的详细实现思路，推荐阅读：MNIST机器学习入门 - TensorFlow 官方文档中文版 - 极客学院Wiki

import tensorflow as tf

# Import MINST data
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

# Parameters
learning_rate = 0.01
training_epochs = 10
batch_size = 100
display_step = 1

# tf Graph Input
x = tf.placeholder(tf.float32, [None, 784])  # mnist data image of shape 28*28=784
y = tf.placeholder(tf.float32, [None, 10])  # 0-9 digits recognition => 10 classes

# Set model weights
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))

# Construct model
pred = tf.nn.softmax(tf.matmul(x, W) + b)  # Softmax

# Minimize error using cross entropy
cost = tf.negative(tf.reduce_sum(y * tf.log(pred)))
# Gradient Descent
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)

# Initializing the variables
init = tf.global_variables_initializer()
# Launch the graph
with tf.Session() as sess:
    sess.run(init)

    # Training cycle
    for epoch in range(training_epochs):
        avg_cost = 0.
        total_batch = int(mnist.train.num_examples / batch_size)
        # Loop over all batches
        for i in range(total_batch):
            batch_xs, batch_ys = mnist.train.next_batch(batch_size)
            # Fit training using batch data
            _, c = sess.run([optimizer, cost], feed_dict={x: batch_xs,
                                                          y: batch_ys})
            # Compute average loss
            avg_cost += c / total_batch
        # Display logs per epoch step
        if (epoch + 1) % display_step == 0:
            print("Epoch:", '%04d' % (epoch + 1), "cost=", "{:.9f}".format(avg_cost))

    print("Optimization Finished!")

    # Test model
    correct_prediction = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))
    # Calculate accuracy for 3000 examples
    accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
    print("Accuracy:", accuracy.eval({x: mnist.test.images, y: mnist.test.labels}))