数值计算方法实验之newton多项式插值 (Python 代码)

一、实验目的

在己知f(x),x∈[a,b]的表达式，但函数值不便计算或不知f(x),x∈[a,b]而又需要给出其在[a,b]上的值时,按插值原则f(x_i)=y_i (i=0,1,……, n)求出简单函数P(x)(常是多项式)，使其在插值基点x_i处成立(x_i)= y_i(i=0,1,……,n),而在[a,b]上的其它点处成立f(x)≈P(x).

二、实验原理

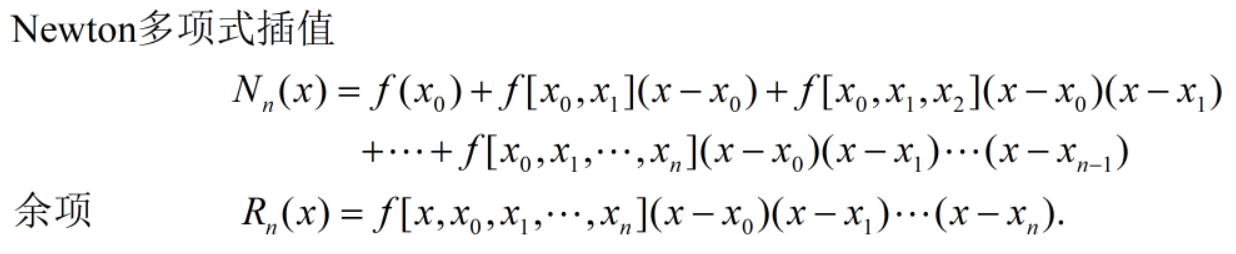
三、实验内容

求f(x)=x⁴在[0,2]上按5个等距节点确定的Lagrange插值多项式

四、实验程序

import matplotlib.pyplot as plt
from pylab import mpl
import math

x = [0, 0.5, 1, 1.5, 2]
y = [0, 0.0625, 1, 5.0625, 16]

"""计算四次差商的值"""
def four_order_difference_quotient(x, y):
    # i记录计算差商的次数，这里循4次，计算4次差商。
    i = 0
    quotient = [0, 0, 0, 0, 0]
    while i < 4:
        j = 4
        while j > i:
            if i == 0:
                quotient[j]=((y[j]-y[j-1])/(x[j]-x[j-1]))
            else:
                quotient[j] = (quotient[j]-quotient[j-1])/(x[j]-x[j-1-i])
            j -= 1
        i += 1
    return quotient;

def function(data):
    return  parameters[0] + parameters[1]*(data-0) + parameters[2]*(data-0)*(data-0.5) + parameters[3]*(data-0)*(data-0.5)*(data-1) + parameters[4]*(data-0)*(data-0.5)*(data-1)*(data-1.5)

"""计算插值多项式的值"""
def calculate_data(x,parameters):
    returnData=[];
    for data in x:
        returnData.append(function(data))
    return returnData

"""画函数的图像
newData为曲线拟合后的曲线
"""

def draw(newData):
    plt.scatter(x,y,label="离散数据",color="blue")
    plt.plot(datax,newData,label="牛顿插值拟合数据",color="orange")
    plt.scatter(1.75,1.75**4, label="准确值",color="red")
    plt.title("牛顿插值法拟合数据")
    mpl.rcParams['font.sans-serif'] = ['SimHei']
    mpl.rcParams['axes.unicode_minus'] = False
    plt.legend(loc="upper left")
    plt.show()

parameters=four_order_difference_quotient(x,y)
datax=[0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1, 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2]
datay=calculate_data(datax,parameters)
draw(datay)
print("牛顿插值多项式为：N(x) = %f(x-0) + %f(x-0)(x-0.5) + %f(x-0)(x-0.5)(x-1) + %f(x-0)(x-0.5)(x-1)(x-1.5)"%(parameters[1], parameters[2], parameters[3],parameters[4]))

五、运算结果

(1) 图像

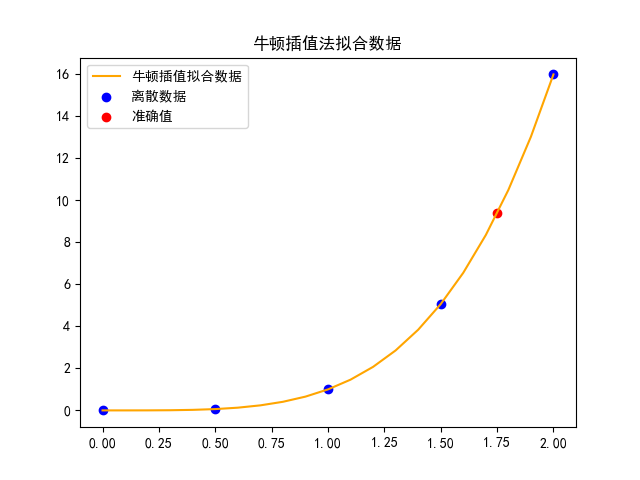
（2）运算结果

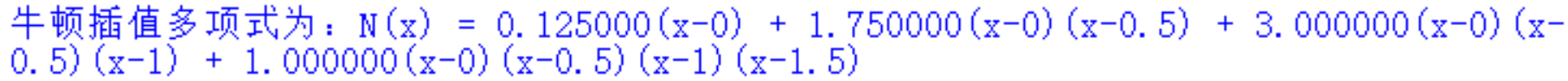
六、心得体会

通过本次实验，我对数值分析有了更深一个层次的认识 ，将数学理论和计算机 软件结合会得到意想不到的结果 比如插值法，在先学习了拉格朗日插值法后，对其理解透彻，了解了其中的原理和思想，再学习之后的牛顿插值以及三次样条插值等等，都很容易的融会贯通，很容易的就理解了其中所想，其中心思想并没有多大的变化，但是使用的方式却是不同的每个不同的思考方式带来的都是不同的算法。

在不断学习的过程中，知识在不断的获取，能力在不断的提升。同时在老师的指导下，我的知识更上一个台阶，总而言之，本次实验演示我受益匪浅。