线性代数的28法则：作为程序员掌握这些API就够用了……

1. 向量 & 矩阵
- 1.1. 问： np.ndarray 与 np.matrix 的区别
- 1.2. 向量空间
2. 算术运算
- 2.1. 为什么线性代数定义的乘积运算不按照加法的规则（按位相乘）进行？
- 2.2. 数组广播（broadcasting）
3. 矩阵乘积
- 3.1. 矩阵与向量的乘积
4. 点积乘法
5. 特殊矩阵
- 5.1. 转置矩阵
  - 5.1.1. 共轭转置
6. 用矩阵表示各种关系
7. 行列式
- 7.1. 行列式的性质
- 7.2. 行列式的计算
8. 逆矩阵 & 秩
9. 线性方程组
10. 特征值 & 特征向量

《程序员的数学3：线性代数》

1. 向量 & 矩阵

向量（数组）的元素类型可以通过dtype属性获得。上面例子中的参数序列的元素都是整数，因此所创建的数组的元素类型也是整数，并且是32bit的长整型。可以通过dtype参数在创建时指定元素类型:

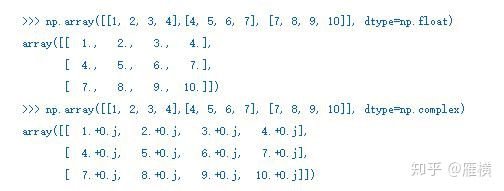
对，向量与 np.ndarray 不是同一个东西——向量就是一维数组。在几何意义上，向量表示的是多维空间中的有向线段，数组的每个数据代表了一个维度的参数。

而 ndarray 可以是多维数组，更像是Matrix。

1.1. 问： `np.ndarray` 与 `np.matrix` 的区别

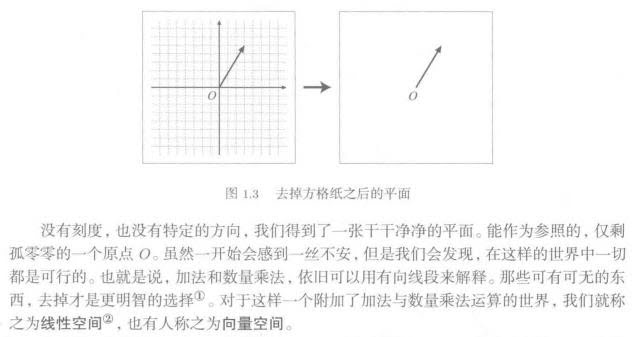
1.2. 向量空间

把上图中的刻度去掉，就是向量空间。

2. 算术运算

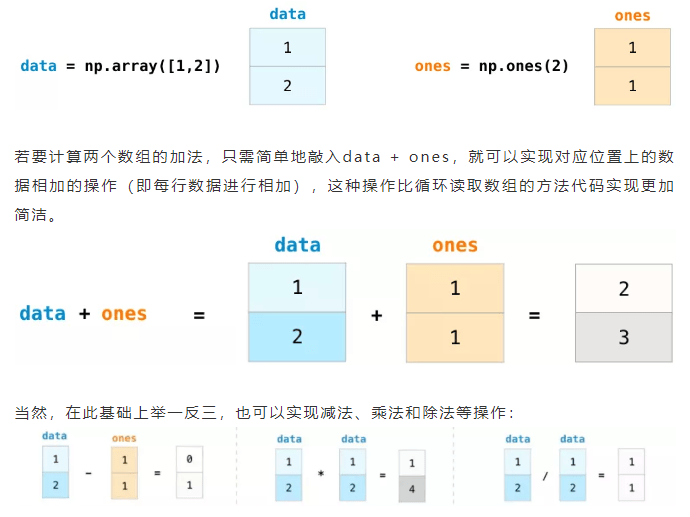
注意：numpy.ndarray的乘积运算，并不等同于线性代数中两个向量的乘积运算。

2.1. 为什么线性代数定义的乘积运算不按照加法的规则（按位相乘）进行？

线性代数的乘法运算（矩阵乘积），几何意义表示坐标系变换。

2.2. 数组广播（broadcasting）

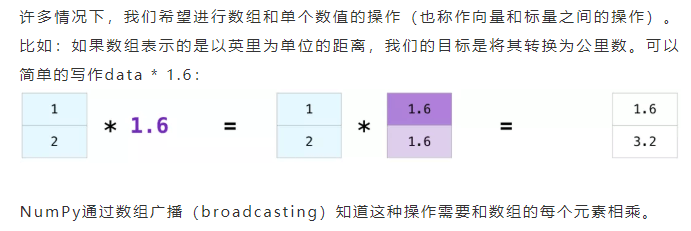
对于不同大小的矩阵，只有两个矩阵的维度同为1时（例如矩阵只有一列或一行），我们才能进行这些算术运算，在这种情况下，NumPy使用广播规则（broadcast）进行操作处理：

3. 矩阵乘积

3.1. 矩阵与向量的乘积

两种情形：

矩阵 * 列向量 = 新向量（列）

在这个过程中，向量代表的是一个有向线段，而矩阵则表示一个转换坐标系（或者称之为“线性的函数映射”），通过乘法运算后，向量被映射成了另一个坐标系中的样子。

所以，看懂了矩阵乘积，就能明白矩阵的本质——“矩阵就是映射”。

3.1.1. 除了坐标转换，矩阵乘积还有什么用？

3.1.2. 矩阵 * 矩阵

矩阵之间相乘，其本质就是映射的合成。

其实上述公式可以做如下转换：

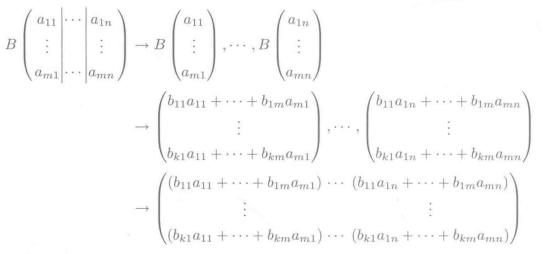
这是啥？其本质就是：

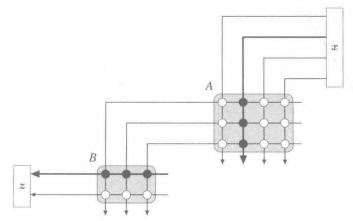
读懂这个本质，就能知道，矩阵乘法符合结合律：

C(BA) = (CB)A

但不符合交换律：

为什么矩阵乘法不符合交换律？

考虑A是一个旋转的坐标变换，而B则代表横向拉伸。那么先旋转后拉伸与先拉伸后旋转，结果当然不同。

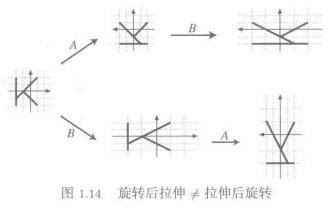
3.1.3. 一些特例

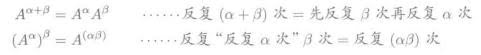
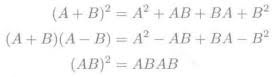
4. 点积乘法

5. 特殊矩阵

零矩阵

零矩阵表示的映射是所有点都映射到原点的映射。
单位矩阵

“什么都没变”的映射。
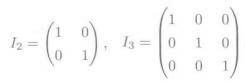
对角矩阵

对角矩阵表示的映射是“沿着坐标轴伸缩”，其中对角元素就是各轴伸缩的倍率。
分块矩阵
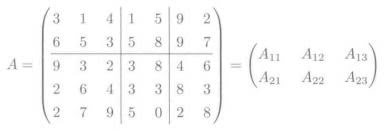
正交矩阵
对称矩阵

5.1. 转置矩阵

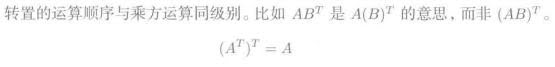
5.1.1. 共轭转置

6. 用矩阵表示各种关系

《程序员的数学3》p53_1.2.10

6.1. 高阶差分

6.2. 高阶微分

6.3. 消除常数项

7. 行列式

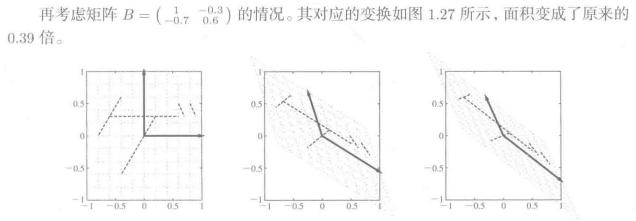
行列式求得的是一个数，几何意义为（面积、体积...）的扩大率。

行列式只针对方阵而言，非方阵矩阵不存在行列式。

7.1. 行列式的性质

常数乘法不变性

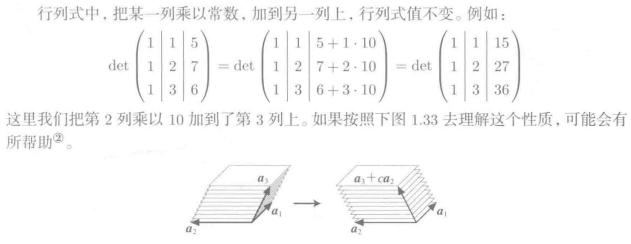
转置矩阵的行列式

多重线性

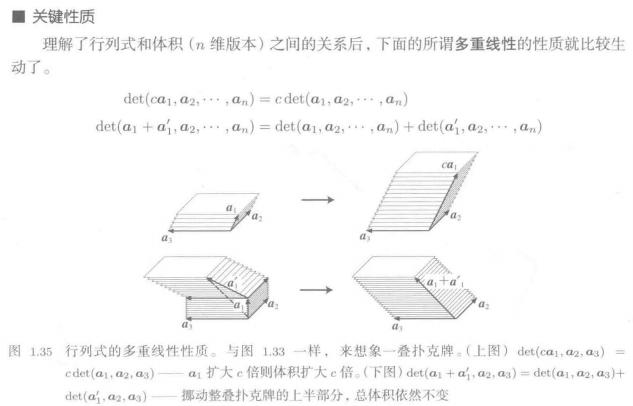
注意：多重性质都是针对1列定义的：

交替性

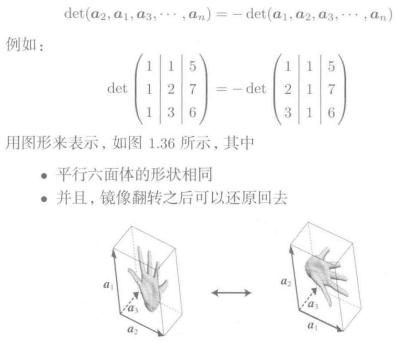
7.2. 行列式的计算

from numpy import linalg

n = linalg.det(A)

8. 逆矩阵 & 秩

如果 y = Ax + b 为 顺问题 ，那么，通过 y 求得 x 的问题就是 逆问题 。

逆矩阵就是把矩阵A映射的向量还原回去的映射。简单的说，就是“逆映射”。

正则矩阵：存在逆矩阵的方阵（可逆矩阵，非奇异矩阵）
奇异矩阵：反之~

8.1. 逆矩阵的性质

8.2. 对角矩阵的逆矩阵

8.3. 求解逆矩阵（numpy）

from numpy import linalg

invA = linalg.inv(A)

8.4. 秩

秩，体现的是不相关的维度数。

8.4.1. “秩”是图像经过矩阵变换之后的空间维度

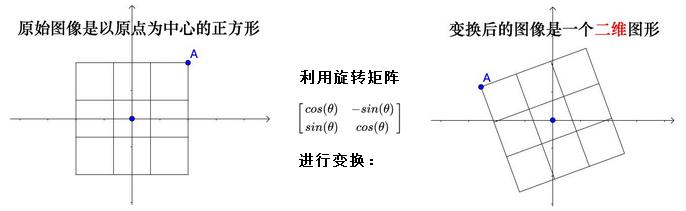
如果经过矩阵 A 变换后的结果是一个平面，空间没有被压缩扁平化，那么该转换可逆，称为非奇异矩阵
非奇异矩阵的秩与列数相等，称之为满秩（Full Rank）矩阵
对于满秩矩阵来说, 变换后唯一落在原点的就是零向量本身

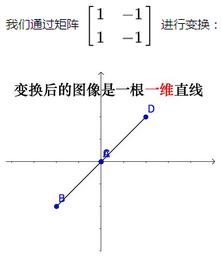
当变换的结果是一条直线，该矩阵是一维的，rank(A) = 1 ，此时矩阵不可逆, 称为奇异矩阵
非满秩矩阵，会将空间压缩到更低的一维直线上，也就是由嫩绿色直线上一系列的向量在变换后成为零向量

当变换的结果是压缩到原点，则该矩阵是零维的，称 rank(A) = 0

8.4.2. “秩”是列空间的维度

“秩”就是矩阵所代表空间的不相关的维度数量。而不相关的的维度才构成空间，所以，“秩”代表空间的维度。

8.4.3. 话说回来，为啥叫做“秩”

知乎: 非叫“秩”不可，有秩才有解

举个例子就很容易理解，大家排队买票。如果大家互相不认识，那就会一个排一个，非常有秩序。然而，如果突然来了一个与队伍前面的人认识的人，这个人又不自觉，非要插队。那后面的人肯定要有意见了，说你要是这样我前面还有认识的人呢，你插我也插，这样整个队伍就乱掉了，谁也买不成。

通过这个例子，可得以下结论：彼此不认识，那就不相关，就有秩序，问题就好解决；反之，彼此相关，就没有秩序，问题就不好解决。

所以，数学家们定义，矩阵中的最大的不相关的向量的个数，就叫秩，可以理解为有秩序的程度。

从社会学的角度在考虑一下，政府机关是讲人际关系的地方，可谓是关系错综复杂，通常都是近亲繁殖。显然，这些部门，用矩阵来说，就不满秩，秩非常小。可以想象这些地方的工作肯定是搞不好的，因为没有秩序。所以想找个好单位，满秩可以作为一项评价指标哦~

8.4.4. 求解秩（numpy）

from numpy import linalg

n = linalg.matrix_rank(A)

8.5. 维数定理

向量空间的维数等于对应矩阵的秩
两个有限维子空间的和的维数定理： dim(U1+U2) = dimU1 + dimU2 - dim(U1 ∩ U2)
两个有限集合元素个数的容斥原理： card(U1∪U2) = cardU1 + cardU2 - card(U1 ∩ U2)

9. 线性方程组

10. 特征值 & 特征向量