FFT,NTT入门

目录

• -1.前置知识
  • 复数
  • 单位根
  • 单位根反演
• 0.卷积
• 1.FFT

-1.前置知识

复数

  复数单位\(i\)：定义为\(i^2=-1\)。\(i\)可以直接参与运算。

  复数：形如\(z=a+bi\)的数被称为复数，其中\(a\)称为实部，\(b\)称为虚部。可以发现，当\(b=0\)的时候，\(z\)就是实数。

  复平面：建立直角坐标系。对于复数\(z=a+bi\)，其在复数平面上的坐标就是\((a,b)\)；即横轴表示实部，纵轴表示虚部。另外，一个复数同样可以被表示为复平面上的一个从原点出发的向量。

  复数的运算：设\(x=a+bi,y=c+di\)，定义如下：

    \(x+y=a+bi+c+di=(a+c)+(b+d)i\)；

    \(x-y=(a+bi)-(c+di)=(a-c)+(b-d)i\)；

    \(xy=(a+bi)(c+di)=ac+(bc+ad)i+bdi^2=(ac-bd)+(bc+ad)i\)

  复数的三角函数形式：前面说到，复数在复平面上即是一个向量。因此我们可以定义复数\(z=a+bi\)的模长为\(|z|=\sqrt{a^2+b^2}\)，即向量对应的模长；定义复数\(z=a+bi\)的幅角为向量到实轴正方向的角度为辐角。



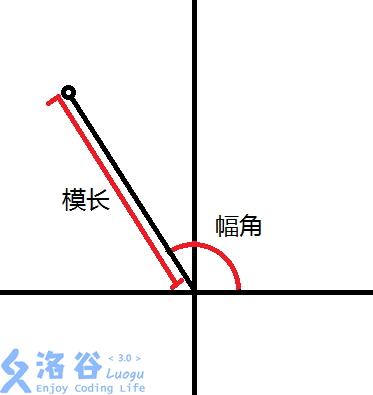
  反过来，我们可以通过模长\(|z|\)与幅角\(\theta\)来唯一确定一个复数，即\(z=|z|(\cos\theta+i\sin\theta)\)。

  因此，对于复数\(x=|x|(\cos\theta_x+i\sin\theta_x),y=|y|(\cos\theta_y+i\sin\theta_y)\)，复数的乘法也等价于：

  \(xy=|x||y|((\cos\theta_x\cos\theta_y-\sin\theta_x\sin\theta_y)+i(\sin\theta_x\cos\theta_y+\sin\theta_y\cos\theta_x))=|x||y|(\cos(\theta_x+\theta_y)+i\sin(\theta_x+\theta_y))\)

  即模长相乘，辐角相加。

单位根

  单位根被定义为：方程\(x^n=1\)在复数域内的所有解。

  莽了？不用担心，我们先聊一聊单位圆。



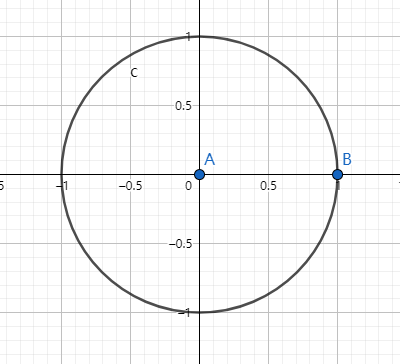
  可以发现，单位圆实际上就是所有的起点在原点且模长为\(1\)的向量的终点集合。

  另一方面，根据复数运算性质，我们发现，所有解的模长一定是\(1\)。

  再想一想，解的辐角应该是：\(\frac{2\pi\times 0}{n},\frac{2\pi\times 1}{n},...,\frac{2\pi\times (n-1)}n\)，只有这些向量自乘\(n\)次之后，才会落到实轴正半轴上来。

  因此，我们得到了结果：\(n\)次单位根有\(n\)个，记为\(\omega_n^{0\sim(n-1)}\)，其中\(\omega_n^k\)为一个模长为\(1\)，辐角为\(\frac{2\pi\times k}{n}\)的复数。

  下图展示了\(n=3\)时的单位根（们）：



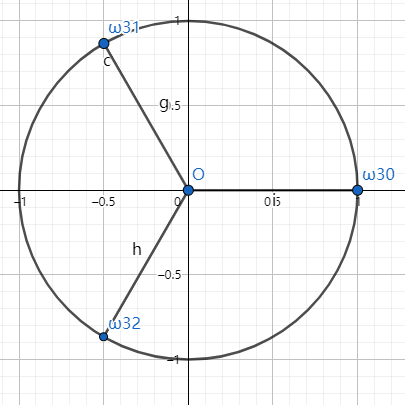
  接下来，有一些关于单位根的重要性质，大家可以按照切蛋糕来理解。

    1.\(\omega_n^k=(\omega_n^1)^k\)，证明略；

    2.\(\omega_n^j\times\omega_n^k=\omega_n^{j+k}\)，可用上式证明；

    3.\(\omega_{2n}^{2k}=\omega_n^k\)。比如，你一次在蛋糕上切\(\frac18\)，那么你切\(4\)块就可以得到半块蛋糕；一次切\(\frac14\)，那么你就需要\(2\)块。

    4.折半引理：当\(n\)为偶数的时候，\(\omega_{n}^{(k+\frac n2)}=-\omega_n^k\)。其中\(\omega_n^{(k+\frac n2)}=\omega_n^k\times\omega_n^{\frac n2}\)，也就是将\(\omega_n^k\)再转半圈之后得到的向量。此时它们模长相等，方向相反，它们就是相反数。

单位根反演

  定理：

\[\frac1n\sum_{k=0}^{n-1}\omega_n^{ak}=[n|a]
\]

  证明：

  当\(n|a\)的时候：

    设\(a=nt\)，原式中所有\(\omega_n^{ak}=\omega_n^{ntk}=\omega_n^0=1\)，因此原式\(=\frac1n\sum_{k=0}^{n-1}1=1\)。

  当\(n\not|a\)的时候：

    等比数列求和：

\[\begin{aligned}
\frac1n\sum_{k=0}^{n-1}\omega_n^{ak}&=\frac1n\sum_{k=0}^{n-1}(\omega_n^a)^k\\
&=\frac1n\times \frac{1-\omega_n^{an}}{1-\omega_n^a}\\
&=\frac1n\times \frac{1-1}{1-\omega_n^1}\\
&=0
\end{aligned}\]

  于是就证完了。

0.卷积

  卷积是定义在函数上的运算。

  对于函数\(f(n)\)和\(g(n)\)，其卷积\((f*g)(n)\)就是：

\[(f*g)(n)=\int_{-\infty}^{\infty}f(\tau)g(n-\tau)\text d\tau
\]

  我知道你觉得它很没用，所以这里还有离散的表达：

\[(f*g)(n)=\sum_{\tau=-\infty}^{\infty}f(\tau)g(n-\tau)
\]

  你说计算机处理不了实数？好吧，这里还有最后一个，定义在有限序列\(f\)和\(g\)上的卷积：

\[(f*g)(n)=\sum_{i=0}^nf(i)g(n-i)
\]

  是不是很熟悉？这就是我们常见的多项式乘法！

  因此，算法竞赛中常常用卷积优化算法 FFT 来进行多项式乘法运算。

1.FFT