无损卡尔曼滤波UKF(3)-预测-生成Sigma点

无损卡尔曼滤波UKF（3）-预测-生成Sigma点

1 选择创建Sigma点

A 根据

已知上一个时间戳迭代出来的

后验状态 \(x_{k|k}\) 和后验协方差矩阵 \(P_{k|k}\)

他们代表当前状态的分布。

Sigma点的数量取决于状态向量的维度

\(n_{\sigma} = 2\cdot n_x + 1\)

如果以两个维度的状态向量为例。就可以生成五个sigma点。

\(X_{k|k} = [P1,P2,P3,P4,P5]\)

矩阵的每一列都代表一个Sigma点。

\(X_{k|k} = [x_{k|k},x_{k|k}+\sqrt[2]{(\lambda+n_x)P_{k|k}},x_{k|k}-\sqrt[2]{(\lambda+n_x)P_{k|k}} ]\)

关于Lambda,是一个设计的参数，一般情况下，按下面的设置，效果还不错

\(\lambda = 3 - n_x\)

求矩阵的平方根 => 找到矩阵A

\(A = \sqrt[2]{P_{k|k}} <= A^T A = P_{k|k}\)

第一个点就是状态向量的均值。

如果Lambda值大,Sigma点会距离均值点远一些。

生成Sigma点的代码（1）

/*
    根据上述公式，完成生成Sigma点的函数
*/
void UKF::GenerateSigmaPoints(MatrixXd* Xsig_out) {

  // 设置状态向量的维度
  int n_x = 5;

  // 定义传播参数
  double lambda = 3 - n_x;

  // 给定一个样例状态
  VectorXd x = VectorXd(n_x);
  x <<   5.7441,
         1.3800,
         2.2049,
         0.5015,
         0.3528;

  // 给定一个样例状态的协方差矩阵
  MatrixXd P = MatrixXd(n_x, n_x);
  P <<     0.0043,   -0.0013,    0.0030,   -0.0022,   -0.0020,
          -0.0013,    0.0077,    0.0011,    0.0071,    0.0060,
           0.0030,    0.0011,    0.0054,    0.0007,    0.0008,
          -0.0022,    0.0071,    0.0007,    0.0098,    0.0100,
          -0.0020,    0.0060,    0.0008,    0.0100,    0.0123;

  // 创建Sigma点的矩阵、一列代表一个Sigma点、
  MatrixXd Xsig = MatrixXd(n_x, 2 * n_x + 1);

  // 计算矩阵P的平方根
  MatrixXd A = P.llt().matrixL();

  // 设置Sigma矩阵的第一列，一列代表一个Sigma点
  Xsig.col(0) = x;

  // 设置Sigma矩阵剩下的点
  for (int i = 0; i < n_x; ++i) {
    Xsig.col(i+1)     = x + sqrt(lambda+n_x) * A.col(i);
    Xsig.col(i+1+n_x) = x - sqrt(lambda+n_x) * A.col(i);
  }

  // 打印结果
  std::cout << "Xsig = " << std::endl << Xsig << std::endl;

  // 返回结果
  *Xsig_out = Xsig;
}

B 扩充后创建Sigma点

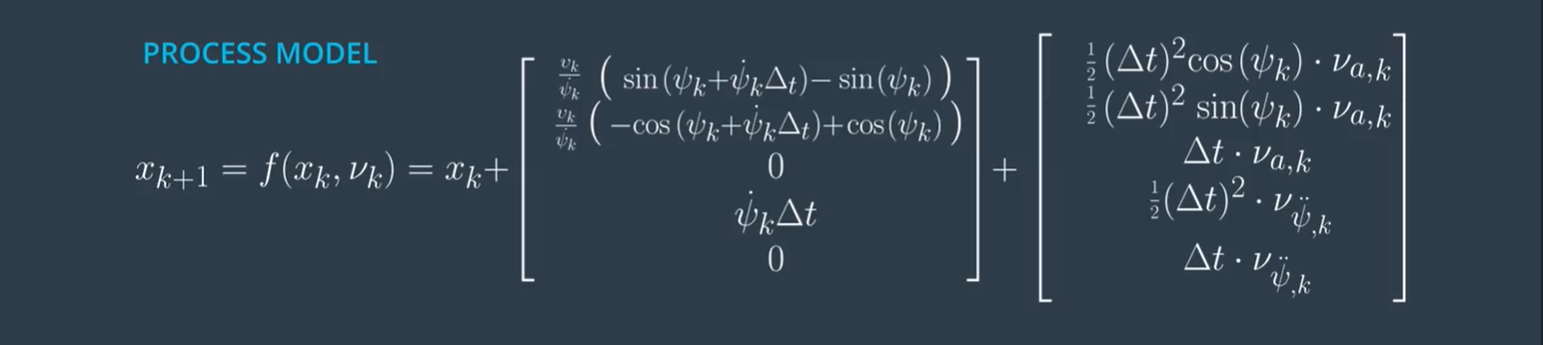
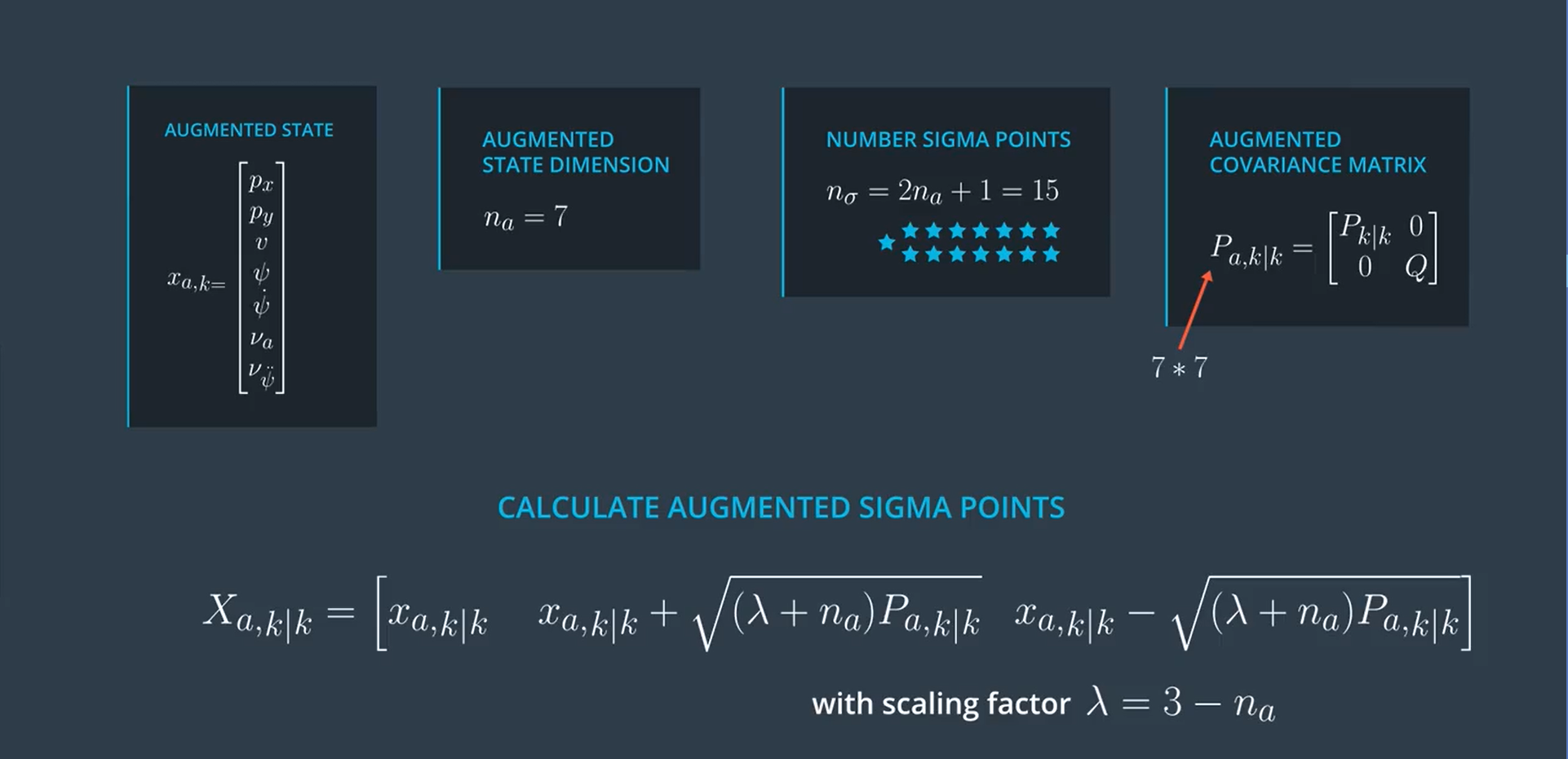
考虑到噪声的影响？？

1. 扩充状态的平均值中添加了两个噪声值。
2. 纵向加速度项和角加速度项。均值为0 ，一定方差的正态分布。
3. 他们的平均值为零，因此在平均状态的Sigma点，将他们的值设置为零。
4. 用零填充扩充的协方差矩阵。
5. 然后，使用topLeftcorner函数设置扩充的协方差矩阵的左上块。
6. 方差放入增强矩阵的右下块。 该2x2块对应于矩阵QQ。

除了这次创建了更多的sigma点，其余部分与以前完全相同。

void UKF::AugmentedSigmaPoints(MatrixXd* Xsig_out) {

  // 维数
  int n_x = 5;

  // 扩展后维数为7
  int n_aug = 7;

  // Process noise standard deviation longitudinal acceleration in m/s^2
  double std_a = 0.2;

  // Process noise standard deviation yaw acceleration in rad/s^2
  double std_yawdd = 0.2;

  // 定义传播参数
  double lambda = 3 - n_aug;

  VectorXd x = VectorXd(n_x);
  x <<   5.7441,
         1.3800,
         2.2049,
         0.5015,
         0.3528;

  MatrixXd P = MatrixXd(n_x, n_x);
  P <<     0.0043,   -0.0013,    0.0030,   -0.0022,   -0.0020,
          -0.0013,    0.0077,    0.0011,    0.0071,    0.0060,
           0.0030,    0.0011,    0.0054,    0.0007,    0.0008,
          -0.0022,    0.0071,    0.0007,    0.0098,    0.0100,
          -0.0020,    0.0060,    0.0008,    0.0100,    0.0123;

  // 创建扩充后的平均值向量
  VectorXd x_aug = VectorXd(7);

  // 创建扩充后的状态协方差矩阵
  MatrixXd P_aug = MatrixXd(7, 7);

  // 创建扩充后的Sigma矩阵

  MatrixXd Xsig_aug = MatrixXd(n_aug, 2 * n_aug + 1);

  // 设置扩充后的平均值向量的参数值
  x_aug.head(5) = x;
  x_aug(5) = 0;
  x_aug(6) = 0;

  // 设置扩充后的状态协方差矩阵
  P_aug.fill(0.0);
  P_aug.topLeftCorner(5,5) = P;
  P_aug(5,5) = std_a*std_a;
  P_aug(6,6) = std_yawdd*std_yawdd;

  // 求P的平方根
  MatrixXd L = P_aug.llt().matrixL();

  // 设置Sigma矩阵其他位置的值
  Xsig_aug.col(0)  = x_aug;
  for (int i = 0; i< n_aug; ++i) {
    Xsig_aug.col(i+1)       = x_aug + sqrt(lambda+n_aug) * L.col(i);
    Xsig_aug.col(i+1+n_aug) = x_aug - sqrt(lambda+n_aug) * L.col(i);
  }

  std::cout << "Xsig_aug = " << std::endl << Xsig_aug << std::endl;

  *Xsig_out = Xsig_aug;
}