P2114 [NOI2014]起床困难综合症【二进制运算+优化】

起床困难综合症【二进制运算+优化】

题目描述

21世纪，许多人得了一种奇怪的病：起床困难综合症，其临床表现为：起床难，起床后精神不佳。作为一名青春阳光好少年，atm一直坚持与起床困难综合症作斗争。通过研究相关文献，他找到了该病的发病原因： 在深邃的太平洋海底中，出现了一条名为drd的巨龙，它掌握着睡眠之精髓，能随意延长大家的睡眠时间。 正是由于drd的活动，起床困难综合症愈演愈烈， 以惊人的速度在世界上传播。为了彻底消灭这种病，atm决定前往海底，消灭这条恶龙。历经千辛万苦，atm终于来到了drd所在的地方，准备与其展开艰苦卓绝的战斗。drd有着十分特殊的技能，他的防御战线能够使用一定的运算来改变他受到的伤害。具体说来，drd的防御战线由n扇防御门组成。每扇防御门包括一个运算op和一个参数t，其中运算一定是OR,XOR,AND中的一种，参数则一定为非负整数。如果还未通过防御门时攻击力为x，则其通过这扇防御门后攻击力将变为x op t。最终drd受到的伤害为对方初始攻击力x依次经过所有n扇防御门后转变得到的攻击力。

由于atm水平有限，他的初始攻击力只能为0到m之间的一个整数（即他的初始攻击力只能在 0, 1, … , m中任选，但在通过防御门之后的攻击力不受m的限制）。为了节省体力，他希望通过选择合适的初始攻击力使得他的攻击能让drd受到最大的伤害，请你帮他计算一下，他的一次攻击最多能使drd受到多少伤害。

输入格式

输入文件的第 1 行包含 2 个整数，依次为n, m，表示 drd 有n扇防御门，atm 的初始攻击力为0到m之间的整数。

接下来n行，依次表示每一扇防御门。每行包括一个字符串op和一个非负整数t，两者由一个空格隔开，且op在前，t在后，op表示该防御门所对应的操作，t表示对应的参数。

输出格式

输出一行一个整数，表示atm的一次攻击最多使drd受到多少伤害。

输入

3 10

AND 5

OR 6

XOR 7

输出

1

说明/提示

atm可以选择的初始攻击力为 0,1, … ,10。

假设初始攻击力为 4，最终攻击力经过了如下计算

4 AND 5 = 4

4 OR 6 = 6

6 XOR 7 = 1

类似的，我们可以计算出初始攻击力为 1,3,5,7,9 时最终攻击力为 0，初始攻击力为 0,2,4,6,8,10 时最终攻击力为 1，因此atm的一次攻击最多使drd受到的伤害值为1。

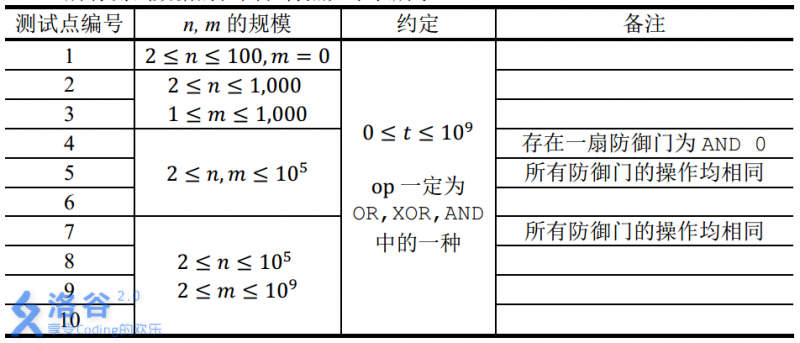
【数据规模与约定】

分析

开始自己用暴力写的，就是纯纯的枚举，当然结果肯定\(T\)了，所以看到标签为dp，但是自己又没有什么好的思路，就看了看书上的分析，这才眼前一亮。

输入当然不用说，但是最好是用结构体或者\(map\)来存，方便使用。由于题目中给出了\(m\)的范围，是\(10^9\)，也就差不多是二进制里的30位，所以我们就可以枚举位数，仔细想一想，要想让结果最大，是不是每一位都是\(1\)才最好呢，所以根据这个我们可以一位一位的扫，每一位都进行要求的\(n\)次运算，一共只需要扫\(30\)次，效率是不是很高呢。然后比较，如果这个二进制串表示的值超过了\(m\)，那么肯定是不能取的，所以只有小于的时候才可以。当这一位是\(1\)的时候，且值不超过\(m\)，显然取这一位是最优的。如果超过了或者没可能为\(1\)，那么就只能是\(0\)了。最后把\(ans\)加起来就好了。总结来说就是一个效率的加快，从依次枚举到只需要把每一位都枚举出来，直接成倍提高效率。

代码

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e5+10;
struct Node{
    char s[4];
    int v;
}a[maxn];
int n,m;
int cale(int bit,int now){//对第bit位进行n次运算，算出这一位的结果为1或0
    for(int i=1;i<=n;++i){
        int x=a[i].v >> bit & 1;//把当前位左边和右边全部置空，以便于只对当先bit位运算
        if(a[i].s[0] == 'A')now &= x;
        else if(a[i].s[0] == 'O') now |= x;
        else now ^= x;
    }
    return now;
}
int main(){
    int ans = 0;
    cin>>n>>m;
    for(int i=1;i<=n;++i){
        cin>>a[i].s>>a[i].v;
    }
    int res1,res0;
    int val = 0;
    for(int bit=29;bit>=0;--bit){//枚举第几位
        res0 = cale(bit,0);//0经过n次运算后的结果
        res1 = cale(bit,1);//1经过n次运算后的结果
        if(val+(1<<bit) <=m && res0 < res1){//当前位取1不超过m且当前位运算后有1的情况
            val += 1<<bit;//记录整个二进制数的大小，不能超过m
            ans+=res1<<bit;
        }
        else ans += res0<<bit;//超过m或者都为0
    }
    cout<<ans<<endl;
}