算法：模拟退火（基于c++程序）

一　什么是模拟退火算法？

• 所谓退火,其实是金属冶炼的一个名词.比如加工一把刀,我们通常是把材料加工到很高的一个温度,加以锤炼.之后慢慢的将温度降下来,如果我们降温的控制比较好的话,那么金属里面的原子就更加偏向于形成能量比较低的状态,如果一个粒子能量很低,他的稳定性会更强,不易受到损坏.刀会更锋利,韧性更足.
• 当一个函数问题比较复杂的时候,无法通过直接微分求出.因为受到退火的启发,我们就可以通过这个算法求出一个复杂函数的极值问题.

二 模拟退火算法原理(策略)

比如先看第一种情况(粉色),X(n)变化到X(n+1)时,可以是温度(能量)下降的,这个是百分百是允许的,因为我的目的是让他下降的(好像是废话哎…).但这就带来了一个问题,X(n+1)可能会陷入一个局部最优解,不能正确的找到全局最优.

因此,我们必须允许一定的概率产生第二种情况(红色)来跳出局部最优解.这个概率与温度(能量)有很大的关系,温度越高,往上蹦的概率也越大,蹦得高度也越大,这样它有可能跳出局部最优解,从而陷入更深的坑里面去(因此就可能是全局最优啦).因此蹦进小坑可能会出来,但进入大坑再出来的可能性就很小,通过这样迭代,就可以找到全局最优解.

因此,初始温度越高,退火过程越慢,越容易得到全局最优,当然这样花费的时间越长,这也是必须付出的代价.

三 公式

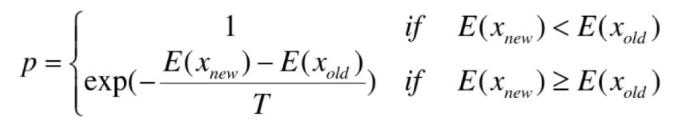
这下来看看公式,当从 X(n) 变化到 X(n+1) 时,能量 E 如果是下降的,让它产生这个概率为1.当从 X(n) 变化到 X(n+1) 时,能量 E 如果是 上升的,这个概率是 exp(-(E(new)-E(old))/T) .因此温度越大 ,概率越高.温度越低,往上蹦的概率越低.

模拟退火一般有两个循环过程来组成:

在外循环里面，每一次迭代温度都会改变。

T(n)= λT(n-1) ,其中 λ 是一个小于1的数,一 般取值在0.8-0.99之间,使得对每一温度,都有足够的次数去尝试.收敛速度比较慢.

在内循环里面,以一定规则在当前状态附近产生新的状态 x(n) 产生 x’(n) ，计算 f(x(n)) 和 f(x’(n)) . 得到

Δf=f(x’(n))-f(x(n)) .

如果 Δf<0 , 说明 x’(n) 好于 x(n) ,因此 x(n+1)=x’(n) . 如果 Δf>0, 计算 p , 产生一个随机数 α ,若 p>α .则接受 x’(n) 为 下一个状态值 , x(n+1)=x’(n) . 否则拒绝 x’(n) . x(n+1)=x(n) .

根据内循环终止准则，检查是否达到热平衡。按照公式调整温度，根据外循环终止准则检查退火算法是否收敛。 外循环终止的准则也可以设置为固定的迭代次数，达到该次数以后系统即停止计算。

四 代码(旅行商问题)

//模拟退火
#include<iostream>
#include<string.h>
#include<time.h>
#include<math.h>
#define T_start 100000 //初始温度
#define T_end (1e-9)
#define q 0.95 //退火系数
#define L 1000 //每个温度时的迭代次数
#define N 52//数组的行数
int city_l[N];//用于存放一个解
double city_p[N][2] = { { 565,575 },{ 25,185 },{ 345,750 },{ 945,685 },{ 845,655 },//每个城市的坐标
{ 880,660 },{ 25,230 },{ 525,1000 },{ 580,1175 },{ 650,1130 },{ 1605,620 },
{ 1220,580 },{ 1465,200 },{ 1530,5 },{ 845,680 },{ 725,370 },{ 145,665 },
{ 415,635 },{ 510,875 },{ 560,365 },{ 300,465 },{ 520,585 },{ 480,415 },
{ 835,625 },{ 975,580 },{ 1215,245 },{ 1320,315 },{ 1250,400 },{ 660,180 },
{ 410,250 },{ 420,555 },{ 575,665 },{ 1150,1160 },{ 700,580 },{ 685,595 },
{ 685,610 },{ 770,610 },{ 795,645 },{ 720,635 },{ 760,650 },{ 475,960 },
{ 95,260 },{ 875,920 },{ 700,500 },{ 555,815 },{ 830,485 },{ 1170,65 },
{ 830,610 },{ 605,625 },{ 595,360 },{ 1340,725 },{ 1740,245 } };
//计算两座城市距离
double distance(double* city1, double* city2) {
	double x1 = *city1;
	double y1 = *(city1 + 1);
	double x2 = *city2;
	double y2 = *(city2 + 1);
	double dis = sqrt((x1 - x2)*(x1 - x2) + (y1 - y2)*(y1 - y2));
	return dis;
}
//计算从第一个到最后一个的路径长度
double path_len(int* arr) {
	double path = 0;
	int index = *arr;//定位至第一个城市
	for (int i = 0; i < N - 1; i++) {
		int index1 = *(arr + i); int index2 = *(arr + i + 1);
		double dis = distance(city_p[index1 - 1], city_p[index2 - 1]);
		path += dis;
	}
	int last_index = *(arr + N - 1);//最后一个城市序号
	int first_index = *arr;//第一个城市序号
	double last_dis = distance(city_p[last_index - 1], city_p[first_index - 1]);
	path += last_dis;
	return path;
} //初始化函数
void init() {
	for (int i = 0; i < N; i++)
		city_l[i] = i + 1;//初始化一个解
}
//产生一个新解，采用随机交叉两个位置的方式产生新的解
void create_new() {
	double r1 = ((double)rand()) /(double)(RAND_MAX + 1.0);
	double r2 = ((double)rand()) / (double)(RAND_MAX + 1.0);
	int pos1 = (int)(N*r1);
	int pos2 = (int)(N*r2);
	int temp = city_l[pos1];
	city_l[pos1] = city_l[pos2];
	city_l[pos2] = temp;
}
int main() {
	srand((unsigned)time(NULL));//初始化随机数种子
	time_t start, finish;//计算算法持续时间
	start = clock();
	double T = T_start;
	int count = 0;//记录降温次数
	init();//随便初始化一个值
	int city_l_copy[N];//用于保存原始解
	double f1, f2, df;
	double r;
	while (T > T_end) {//温度低于结束温度时，退火结束
		for (int i = 0; i < L; i++) //迭代L次
		{
			//复制数组
			memcpy(city_l_copy, city_l, N * sizeof(int));
			create_new();//产生新解
			f1 = path_len(city_l_copy);
			f2 = path_len(city_l);
			df = f2 - f1;
			/*
			如果df<0,那么结果取最小的就是city_1,不做任何。
			如果df>=0,那么
			*/

		 if (df <= 0) {
				r = ((double)rand()) / (RAND_MAX);
				if (exp(-df / T) >=r) {//保留原解
					memcpy(city_l, city_l_copy, N * sizeof(int));
				}
			}
		}
		T *= q;//降温0
		count++;
	}
	finish = clock();
	double duration = ((double)(finish - start)) / CLOCKS_PER_SEC;//持续时间
	double len = path_len(city_l);
	printf("初始温度 T=%d,降温系数 q=%.2f，每个温度迭代%d 次\n", T_start, q, L, count);
	printf("最优路径长度为：%lf\n程序耗时： %lf\n最优路径为：\n", len, duration);
	for (int i = 0; i < N - 1; i++) {
		printf("%d->", city_l[i]);
	}
	printf("%d\n", city_l[N - 1]);
	return 0;
}

。

五 应用

本算法多应用在神经网络的研究中,其他类似的算法包括蚁群算法,遗传算法等将在以后博客里再讲述.