如何用Python实现常见机器学习算法-2

二、逻辑回归

1、代价函数

可以将上式综合起来为：

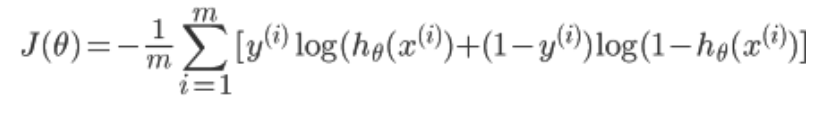
其中：

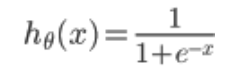
为什么不用线性回归的代价函数表示呢？因为线性回归的代价函数可能是非凸的，对于分类问题，使用梯度下降很难得到最小值，上面的代价函数是凸函数的图像如下，即y=1时：

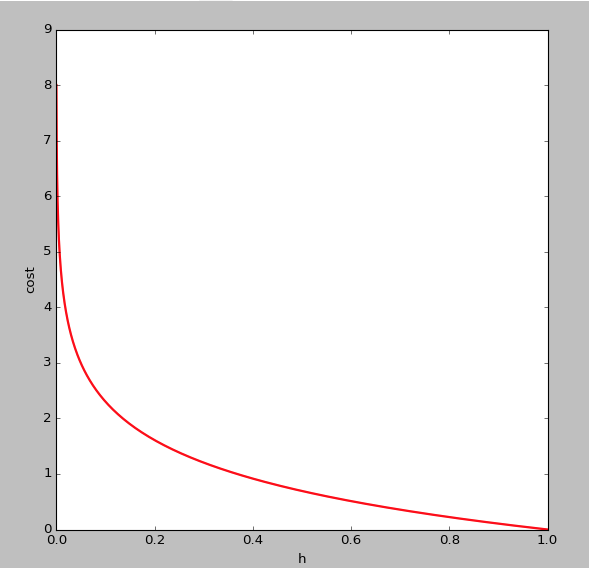
可以看出，当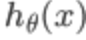趋于1，y=1，与预测值一致，此时付出的代价cost趋于0，若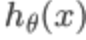趋于0，y=1，此时的代价cost值非常大，我们最终的目的是最小化代价值，同理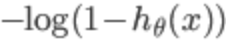的图像如下（y=0）：

2、梯度

同样对代价函数求偏导：

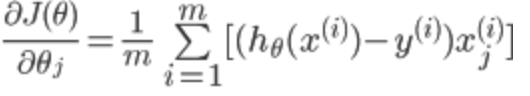
可以看出与线性回归的偏导数一致。

推导过程：

3、正则化

正则化的目的为了防止过拟合。在代价函数中加上一项

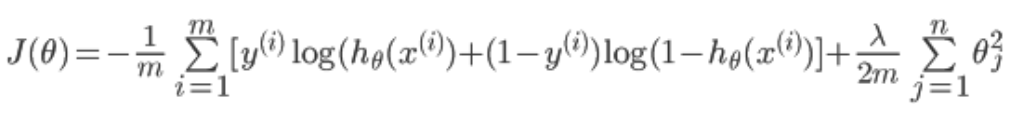
注意j是从1开始的，因为theta(0)为一个常数项，X中最前面一列会加上一列1，所以乘积还是theta(0)，与feature没有关系，没有必要正则化。

正则化后的代价：

 # 代价函数
 def costFunction(initial_theta,X,y,inital_lambda):
     m = len(y)
     J = 0

     h = sigmoid(np.dot(X,initial_theta))    # 计算h(z)
     theta1 = initial_theta.copy()           # 因为正则化j=1从1开始，不包含0，所以复制一份，前theta(0)值为0
     theta1[0] = 0   

     temp = np.dot(np.transpose(theta1),theta1)
     J = (-np.dot(np.transpose(y),np.log(h))-np.dot(np.transpose(1-y),np.log(1-h))+temp*inital_lambda/2)/m   # 正则化的代价方程
     return J

正则化后的代价的梯度

 # 计算梯度
 def gradient(initial_theta,X,y,inital_lambda):
     m = len(y)
     grad = np.zeros((initial_theta.shape[0]))

     h = sigmoid(np.dot(X,initial_theta))# 计算h(z)
     theta1 = initial_theta.copy()
     theta1[0] = 0

     grad = np.dot(np.transpose(X),h-y)/m+inital_lambda/m*theta1 #正则化的梯度
     return grad  

4、S型函数（即）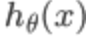

代码实现

 # S型函数
 def sigmoid(z):
     h = np.zeros((len(z),1))    # 初始化，与z的长度一置

     h = 1.0/(1.0+np.exp(-z))
     return h 

5、映射为多项式

因为数据的feature可能很少，导致偏差大，所以创造出一些组合feature

eg:映射为2次方的形式为：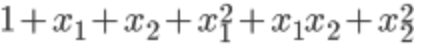

代码实现：

 # 映射为多项式
 def mapFeature(X1,X2):
     degree = 3;                     # 映射的最高次方
     out = np.ones((X1.shape[0],1))  # 映射后的结果数组（取代X）
     '''
     这里以degree=2为例，映射为1,x1,x2,x1^2,x1,x2,x2^2
     '''
     for i in np.arange(1,degree+1):
         for j in range(i+1):
             temp = X1**(i-j)*(X2**j)    #矩阵直接乘相当于matlab中的点乘.*
             out = np.hstack((out, temp.reshape(-1,1)))
     return out

6、使用scipy的优化方法

梯度下降使用scipy中optimize中的fmin_bfgs函数

调用scipy中的优化算法fmin_bfgs(拟牛顿法Broyden-Fletcher-Goldfarb-Shanno costFunction是自己实现的一个求代价的函数)，

initial_theta表示初始化的值，

fprime指定costFunction的梯度

args是其余参数，以元组的形式传入，最后会将最小化costFunction的theta返回

result = optimize.fmin_bfgs(costFunction, initial_theta, fprime=gradient, args=(X,y,initial_lambda)) 

7、运行结果

data1决策边界和准确度

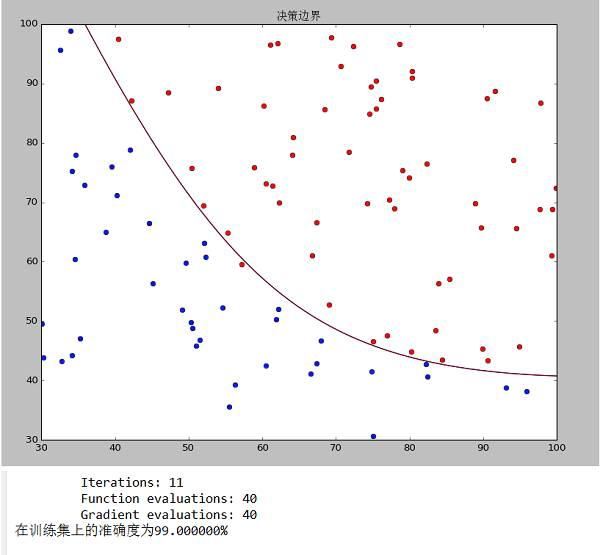
data2决策边界和准确度

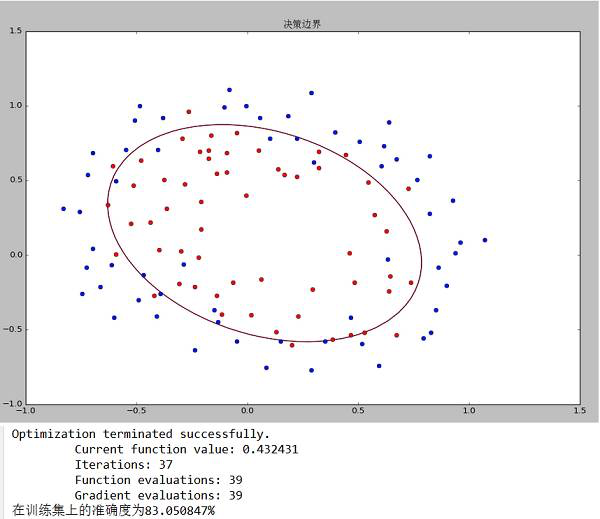
8、使用scikit-learn库中的逻辑回归模型实现

 from sklearn.linear_model import LogisticRegression
 from sklearn.preprocessing import StandardScaler
 from sklearn.cross_validation import train_test_split
 import numpy as np

 def logisticRegression():
     data = loadtxtAndcsv_data("data1.txt", ",", np.float64)
     X = data[:,0:-1]
     y = data[:,-1]

     # 划分为训练集和测试集
     x_train,x_test,y_train,y_test = train_test_split(X,y,test_size=0.2)

     # 归一化
     scaler = StandardScaler()
     scaler.fit(x_train)
     x_train = scaler.fit_transform(x_train)
     x_test = scaler.fit_transform(x_test)

     #逻辑回归
     model = LogisticRegression()
     model.fit(x_train,y_train)

     # 预测
     predict = model.predict(x_test)
     right = sum(predict == y_test)

     predict = np.hstack((predict.reshape(-1,1),y_test.reshape(-1,1)))   # 将预测值和真实值放在一块，好观察
     print predict
     print ('测试集准确率：%f%%'%(right*100.0/predict.shape[0]))          #计算在测试集上的准确度

 # 加载txt和csv文件
 def loadtxtAndcsv_data(fileName,split,dataType):
     return np.loadtxt(fileName,delimiter=split,dtype=dataType)

 # 加载npy文件
 def loadnpy_data(fileName):
     return np.load(fileName)

 if __name__ == "__main__":
     logisticRegression()

逻辑回归_手写数字识别_OneVsAll

 1、随机显示100个数字

我们没有使用scikit-learn中的数据集，像素是20*20px，彩色图如下：

灰度图为：

代码实现：

 # 显示100个数字
 def display_data(imgData):
     sum = 0
     '''
     显示100个数（若是一个一个绘制将会非常慢，可以将要画的数字整理好，放到一个矩阵中，显示这个矩阵即可）
     - 初始化一个二维数组
     - 将每行的数据调整成图像的矩阵，放进二维数组
     - 显示即可
     '''
     pad = 1
     display_array = -np.ones((pad+10*(20+pad),pad+10*(20+pad)))
     for i in range(10):
         for j in range(10):
             display_array[pad+i*(20+pad):pad+i*(20+pad)+20,pad+j*(20+pad):pad+j*(20+pad)+20] = (imgData[sum,:].reshape(20,20,order="F"))    # order=F指定以列优先，在matlab中是这样的，python中需要指定，默认以行
             sum += 1

     plt.imshow(display_array,cmap='gray')   #显示灰度图像
     plt.axis('off')
     plt.show()

2、OneVsAll

如何利用逻辑回归解决多分类的问题，OneVsAll就是把当前某一类看成一类，其他所有类别看作一类，这样就成了二分类问题。如下图，把途中的数据分成三类，先把红色的看成一类，把其他的看作另一类，进行逻辑回归，然后把蓝色的看成一类，其他的看成另一类，以此类推。。。

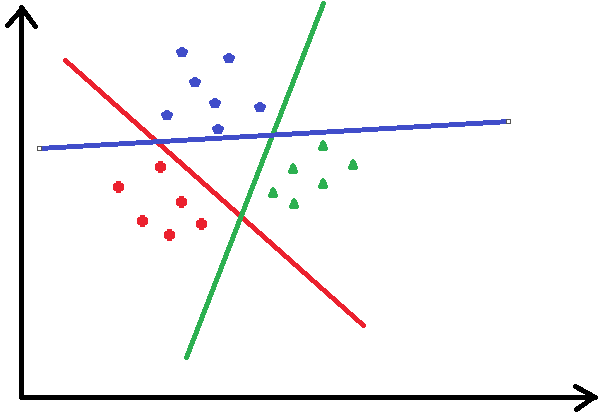
可以看出大于2类的情况下，有多少类就要进行多少次的逻辑回归分类

3、手写数字识别

共有0-9，10个数字，需要10次分类

由于数据集y给出的是0，1，2，。。。9的数字，而进行逻辑回归需要0/1的label标记，所以需要对y处理。

说一下数据集，前500个是0，500-1000是1，...，所以如下图，处理后的y，前500行的第一列是1，其余都是0，500-1000行第二列是1，其余都是0。。。

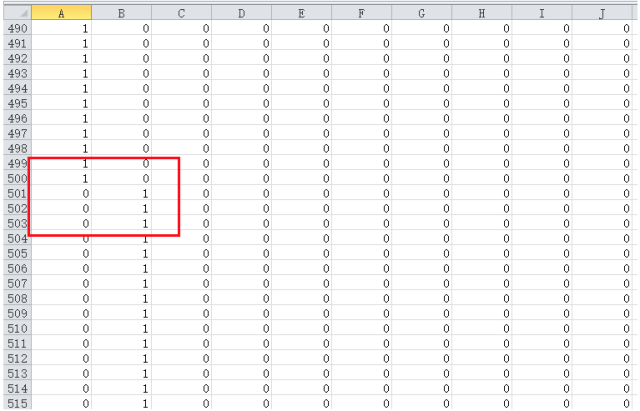
然后调用梯度下降算法求解theta

代码实现：

 # 求每个分类的theta，最后返回所有的all_theta
 def oneVsAll(X,y,num_labels,Lambda):
     # 初始化变量
     m,n = X.shape
     all_theta = np.zeros((n+1,num_labels))  # 每一列对应相应分类的theta,共10列
     X = np.hstack((np.ones((m,1)),X))       # X前补上一列1的偏置bias
     class_y = np.zeros((m,num_labels))      # 数据的y对应0-9，需要映射为0/1的关系
     initial_theta = np.zeros((n+1,1))       # 初始化一个分类的theta

     # 映射y
     for i in range(num_labels):
         class_y[:,i] = np.int32(y==i).reshape(1,-1) # 注意reshape(1,-1)才可以赋值

     #np.savetxt("class_y.csv", class_y[0:600,:], delimiter=',')    

     '''遍历每个分类，计算对应的theta值'''
     for i in range(num_labels):
         result = optimize.fmin_bfgs(costFunction, initial_theta, fprime=gradient, args=(X,class_y[:,i],Lambda)) # 调用梯度下降的优化方法
         all_theta[:,i] = result.reshape(1,-1)   # 放入all_theta中

     all_theta = np.transpose(all_theta)
     return all_theta

4、预测

之前说过，预测的结果是一个概率值，利用学习出来的theta代入预测的S型函数中，每行的最大值就是某个数字的最大概率，所在的列号就是预测的数字的真实值，因为在分类时，所有为0的将y映射在第一列，为1的映射在第二列，以此类推

代码实现：

 # 预测
 def predict_oneVsAll(all_theta,X):
     m = X.shape[0]
     num_labels = all_theta.shape[0]
     p = np.zeros((m,1))
     X = np.hstack((np.ones((m,1)),X))   #在X最前面加一列1

     h = sigmoid(np.dot(X,np.transpose(all_theta)))  #预测

     '''
     返回h中每一行最大值所在的列号
     - np.max(h, axis=1)返回h中每一行的最大值（是某个数字的最大概率）
     - 最后where找到的最大概率所在的列号（列号即是对应的数字）
     '''
     p = np.array(np.where(h[0,:] == np.max(h, axis=1)[0]))
     for i in np.arange(1, m):
         t = np.array(np.where(h[i,:] == np.max(h, axis=1)[i]))
         p = np.vstack((p,t))
     return p

5、运行结果

10次分类，在训练集上的准确度：

6、使用scikit-learn库中的逻辑回归模型实现

 #-*- coding: utf-8 -*-
 from scipy import io as spio
 import numpy as np
 from sklearn import svm
 from sklearn.linear_model import LogisticRegression

 def logisticRegression_oneVsAll():
     data = loadmat_data("data_digits.mat")
     X = data['X']   # 获取X数据，每一行对应一个数字20x20px
     y = data['y']   # 这里读取mat文件y的shape=(5000, 1)
     y = np.ravel(y) # 调用sklearn需要转化成一维的(5000,)

     model = LogisticRegression()
     model.fit(X, y) # 拟合

     predict = model.predict(X) #预测

     print u"预测准确度为：%f%%"%np.mean(np.float64(predict == y)*100)

 # 加载mat文件
 def loadmat_data(fileName):
     return spio.loadmat(fileName)

 if __name__ == "__main__":
     logisticRegression_oneVsAll()