知识点1-树状数组[带poj Stars作为巩固]

转自：https://blog.csdn.net/flushhip/article/details/79165701#commentBox

1.首先其中讲到了一个问题，就是如何求一个数的二进制表示的最末位的1.

int lowbit(x)

{

    return x & -x;

}

用这个即可。假设x=5,那么x的二进制就是0101,-x的二进制1011.（负数补码是除符号位外，从右边起遇到第一个1将其左边取反，并+1）

主要原因是，负数在计算机中是以补码来存储的。所以是这么样子的。（首位表示符号位），运行结果如下：

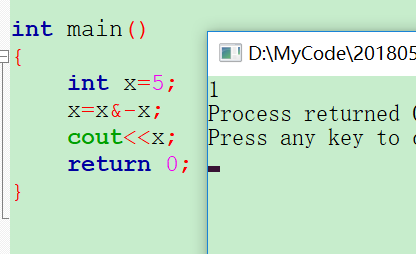
对于x=8来说，也是同样的到离，没毛病。

2.查询前缀和代码

int sum(int x, ArrayInt c, int n)

{

    int ret = ;

    for ( ; x > ; ret += c[x], x -= lowbit(x));

    return ret;

}

//感觉也是比较好理解的，

比如x=6,那么c[x]所包含的和都有谁呢？

lowbit(6)=2，那么只包含两个数即a[5]和a[6].

所以一次for循环之后，ret中是5.6的和；

第二次for循环中，x=4.

lowbit(4)=4，那么即包含1，2，3，4的和，此时ret就包含了1~4的和，返回。

3.更新后缀和

void update(int x, int val, ArrayInt c, int n)

{

    for ( ; x <= n; c[x] += val, x += lowbit(x));

}

比如此时x=5,那么就需要知道如果5被更新了，都有哪个c和需要被更新，

当然首先是5，接着lowbit(5)=1,那么x=6;更新6，接着lowbit(6)=2,x=8；

更新8，此时x=12退出循环。

总:感觉更新后缀和比较难理解。总是就是，查询前缀和是一直-lowbit(x)，更新后缀和就是一直+lowbit(x)即可。

从这里也理解了一些思想，对于数据结构无非就是“增删改查”。针对的就是单点更新，区间查询问题。

最后一张经典图进行理解：

题目

Stars

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 54809		Accepted: 23580

Description

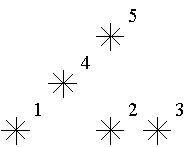
Astronomers often examine star maps where stars are represented by points on a plane and each star has Cartesian coordinates. Let the level of a star be an amount of the stars that are not higher and not to the right of the given star. Astronomers want to know the distribution of the levels of the stars.

For example, look at the map shown on the figure above. Level of the star number 5 is equal to 3 (it's formed by three stars with a numbers 1, 2 and 4). And the levels of the stars numbered by 2 and 4 are 1. At this map there are only one star of the level 0, two stars of the level 1, one star of the level 2, and one star of the level 3.

You are to write a program that will count the amounts of the stars of each level on a given map.

Input

The first line of the input file contains a number of stars N (1<=N<=15000). The following N lines describe coordinates of stars (two integers X and Y per line separated by a space, 0<=X,Y<=32000). There can be only one star at one point of the plane. Stars are listed in ascending order of Y coordinate. Stars with equal Y coordinates are listed in ascending order of X coordinate.

Output

The output should contain N lines, one number per line. The first line contains amount of stars of the level 0, the second does amount of stars of the level 1 and so on, the last line contains amount of stars of the level N-1.

Sample Input

Sample Output

Hint

This problem has huge input data,use scanf() instead of cin to read data to avoid time limit exceed.

//emmm,还是不太会，跟我理解的树状数组不太一样啊！

题目大意：从左到右，从上到下，给出星星的level，星星的level是其左和下所有的星星和。

代码来自：https://blog.csdn.net/ACMer_hades/article/details/46274927

#include<stdio.h>

#include<string.h>

#include<iostream>

#include<algorithm>

using namespace std;

#define maxn 32222

//这道题目很巧妙，首先是根据x的增长来的，然后再根据y的增长来排的；

//所以这样就能理解为什么每次就只要求x之前的就好了

int c[maxn];

int levels[maxn];

int lowbit(int x){

    return x&(-x);

}

//这里是对前x进行求和；

int sum(int x){//求x左边有多少星星。

    int res=;

    while(x>){    //注意这里是x>0,不能写成x>=0;

        res+=c[x];

        x-=lowbit(x);

    }

    return res;

}

//这里的目的是给下标为pos的加上1,这样的话下次询问前面的就能够累加上去了；

void update(int pos){

    while(pos<=){//要加这么多的，所有包含当前的都加进来

        c[pos]++;

        pos+=lowbit(pos);

    }

}

int main(){

    int n,x,y;

    while(~scanf("%d",&n)){

        memset(levels,,sizeof(levels));

        int tt=n;

        while(tt--){

            scanf("%d%d",&x,&y);

            levels[sum(x+)]++;//因为坐标是从0开始的，但是树状数组是从1开始计算，所以+1.

            update(x+);

        }

        for(int i=;i<n;i++) printf("%d\n",levels[i]);

    }

}

//这代码真的很神。

我理解的误区其实就在，数据输入时已经按照y递增，y相同时，x递增来排序了，相当于从底向上，从左向右扫描。

不会出现计数不上的情况。厉害。