Codeforces Round #419 (Div. 2) E. Karen and Supermarket（树形dp）

http://codeforces.com/contest/816/problem/E

题意：

去超市买东西，共有m块钱，每件商品有优惠卷可用，前提是xi商品的优惠券被用。问最多能买多少件商品？

思路：

第一件商品使用优惠券不需要前提，别的都是需要的，然后这样就形成了一棵以1为根的树。

这样，很容易想到是树形dp。

d【u】【j】【0/1】表示以u为根的子数中选择j件商品所需的最少花费，0/1表示u商品是否能用优惠券。

解释一下代码中的sz【】，它所代表的是以u为根的子树的结点数。

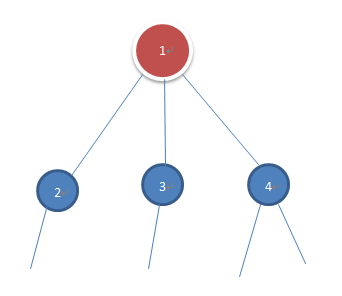
当我们现在访问的是1号结点时，sz【1】=1，然后访问2号结点，2号结点访问结束后，我们就会重新回到1号结点的dfs处，然后进行状态转移

 for(int j=sz[u];j>=;j--)   //表示sz【u】中选取的j个个数

 for(int k=;k<=sz[v];k++)   //表示v结点及其子树中选取的个数

最后将sz【2】的值加到sz【1】中，这样等下一次进行结点3的状态转移时，只需要考虑在2的子树中选取多少个和3的子树中选取多少个即可。到4时，只需要考虑在2和3中一共选取多少个和4的子树中选取多少个，因为前者在上一步已经计算出了最小花费。

 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>
 #include<sstream>
 #include<vector>
 #include<stack>
 #include<queue>
 #include<cmath>
 #include<map>
 #include<set>
 using namespace std;
 typedef long long ll;
 typedef pair<int,int> pll;
 const int INF = 0x3f3f3f3f;
 const int maxn = +;

 int n, m;

 int pa[maxn], pb[maxn];
 int sz[maxn];
 int d[maxn][maxn][];

 vector<int> g[maxn];

 void dfs(int u)
 {
     sz[u]=;
     d[u][][]=, d[u][][]=pa[u], d[u][][]=pa[u]-pb[u];
     for(int i=;i<g[u].size();i++)
     {
         int v=g[u][i];
         dfs(v);

         for(int j=sz[u];j>=;j--)
         {
             for(int k=;k<=sz[v];k++)
             {
                 d[u][j+k][]=min(d[u][j+k][],d[u][j][]+d[v][k][]);
                 d[u][j+k][]=min(d[u][j+k][],min(d[u][j][]+d[v][k][],d[u][j][]+d[v][k][]));
             }
         }
         sz[u]+=sz[v];
     }
 }

 int main()
 {
     //freopen("in.txt","r",stdin);
     while(~scanf("%d%d",&n, &m))
     {
         for(int i=;i<=n;i++)  g[i].clear();
         for(int i=;i<=n;i++)
         {
             scanf("%d%d",&pa[i],&pb[i]);
             if(i>)
             {
                 int x;
                 scanf("%d",&x);
                 g[x].push_back(i);
             }
         }

         memset(d,INF,sizeof(d));
         dfs();

         int i;
         for(i=;i<=n;i++)
         {
             if(min(d[][i][],d[][i][])>m)   break;
         }
         printf("%d\n",i-);
     }
     return ;
 }