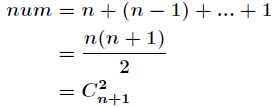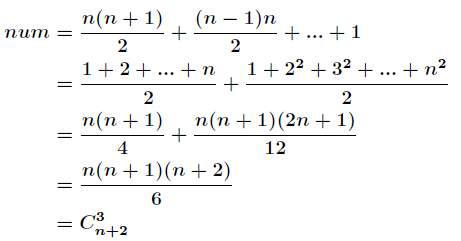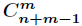组合数取模&&Lucas定理题集

题集链接：

https://cn.vjudge.net/contest/231988

解题之前请先了解组合数取模和Lucas定理

A : FZU-2020 

输出组合数C(n, m) mod p

(1 <= m <= n <= 10^9, m <= 10^4, m < p < 10^9, p是素数)

由于p较大，不可以打表，直接Lucas求解

 #include<iostream>
 using namespace std;
 typedef long long ll;
 const int maxn = 1e5 + ;
 ll fac[maxn];//阶乘打表
 void init(ll p)//此处的p应该小于1e5，这样Lucas定理才适用
 {
     fac[] = ;
     for(int i = ; i <= p; i++)
         fac[i] = fac[i - ] * i % p;
 }
 ll pow(ll a, ll b, ll m)
 {
     ll ans = ;
     a %= m;
     while(b)
     {
         if(b & )ans = (ans % m) * (a % m) % m;
         b /= ;
         a = (a % m) * (a % m) % m;
     }
     ans %= m;
     return ans;
 }
 ll inv(ll x, ll p)//x关于p的逆元，p为素数
 {
     return pow(x, p - , p);
 }
 ll C(ll n, ll m, ll p)//组合数C(n, m) % p
 {
     if(m > n)return ;
     ll up = , down = ;//分子分母;
     for(int i = n - m + ; i <= n; i++)up = up * i % p;
     for(int i = ; i <= m; i++)down = down * i % p;
     return up * inv(down, p) % p;
 }
 ll Lucas(ll n, ll m, ll p)
 {
     if(m == )return ;
     return C(n % p, m % p, p) * Lucas(n / p, m / p, p) % p;
 }
 int main()
 {
     ll n, m, p;
     int T;
     cin >> T;
     while(T--)
     {
         cin >> n >> m >> p;
         //init(p);
         cout<<Lucas(n, m, p)<<endl;
     }
     return ;
 }

B：HDU-3944

求从顶点到达第n行，第m列的元素的最短路径值（最开始是第0行，第0列）

只能向下或者斜向右。

如图，如果在右侧，可以走红色路线，比如第4行第3列，与此对称的是第4行第1列（从第0行，第0列数起）

这样，我们就可以把左侧的转化成右侧来统一计算。中间的也可以这样计算。

左侧转化成右侧：对于n行m列而言，如果m * 2 < n 那么m = n - m

对于右侧的如何计算呢？

用C(x, y)表示x行y列的值，也就是组合数的值

那么ans = C(n , m) + C(n - 1, m) + C(n - 2, m) + ... + C(m + 1, m) + C(m, m) + C(m - 1, m - 1) + C(m - 2, m - 2) + C(0, 0)

红色部分为m

蓝色部分可以通过组合数公式C(n, m) + C(n, m + 1) = C(n +1, m + 1)来计算

把蓝色部分的C(m, m)写成C(m + 1, m + 1)

那么最后两项就可以通过上面那个公式合并成C(m + 2, m + 1)

不断合并，最后得到C(n, m) + C(n, m + 1) = C(n +1, m + 1)

所以答案就是C(n + 1, m + 1) + m % p;

由于计算量大，p的范围是10000内的素数，而需要计算10^6个组合数，所以需要先打表，把10000内的素数筛选出来，打表每个阶乘模上素数的值，还有逆元，这样计算组合数才不会超时，而且数组不能开long long，会超时

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 const int maxn = 1e4 + ;
 int fac[maxn][maxn], inv[maxn][maxn];//阶乘打表 逆元打表
 int prime[maxn], pth[maxn];
 int pow(int a, int b, int m)
 {
     int ans = ;
     a %= m;
     while(b)
     {
         if(b & )ans = (ans % m) * (a % m) % m;
         b /= ;
         a = (a % m) * (a % m) % m;
     }
     ans %= m;
     return ans;
 }
 bool is_prime[maxn];
 void init()
 {
     int n = , cnt = ;
     for(int i = ; i <= n; i++)is_prime[i] = ;
     for(int i = ; i <= n; i++)
     {
         if(is_prime[i])
         {
             prime[++cnt] = i;
             pth[i] = cnt;
             for(int j = i * i; j <= n; j += i)is_prime[j] = ;
         }
     }
     //cout<<cnt<<endl;
     for(int i = ; i <= cnt; i++)
     {
         fac[i][] = inv[i][] = ;
         for(int j = ; j < prime[i]; j++)//大于i的阶乘模上i均为0
         {
             fac[i][j] = fac[i][j - ] * j % prime[i];
             inv[i][j] = pow(fac[i][j], prime[i] - , prime[i]);
         }
     }
 }

 int C(ll n, int m, int p)//组合数C(n, m) % p
 {
     if(m > n)return ;
     if(m == n)return ;
     int t = pth[p];
     return fac[t][n] * (inv[t][m] * inv[t][n - m] % p) % p;
 }

 int Lucas(int n, int m, int p)
 {
     //cout<<n<<" "<<m<<" "<<p<<endl;
     if(m == )return ;
     return C(n % p, m % p, p) * Lucas(n / p, m / p, p) % p;
 }

 int main()
 {
     init();
     int n, m, p;
     int cases = ;
     while(scanf("%d%d%d", &n, &m, &p) != EOF)
     {
         if(m <= n / )
         {
             m = n - m;
         }
         ll ans = (Lucas(n + , m + , p) + m) % p;
         printf("Case #%d: %d\n", ++cases, ans);
     }
     return ;
 }

C:ZOJ-3557

在n个元素的集合中取出lm和不相邻元素的种数

插空法，由于不相邻，那就把这m个先取出来，放在剩下的n-m个数字的两侧的空位上，那么这m个一定不相邻。

等价于n-m+1中放m个元素

C（n - m + 1, m） % p

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 const int maxn = 1e6 + ;
 const int mod = 1e9 + ;
 ll pow(ll a, ll b, ll m)
 {
     ll ans = ;
     a %= m;
     while(b)
     {
         if(b & )ans = (ans % m) * (a % m) % m;
         b /= ;
         a = (a % m) * (a % m) % m;
     }
     ans %= m;
     return ans;
 }
 ll inv(ll x, ll p)//x关于p的逆元，p为素数
 {
     return pow(x, p - , p);
 }
 ll C(ll n, ll m, ll p)//组合数C(n, m) % p
 {
     if(m > n)return ;
     ll up = , down = ;//分子分母;
     for(int i = n - m + ; i <= n; i++)up = up * i % p;
     for(int i = ; i <= m; i++)down = down * i % p;
     return up * inv(down, p) % p;
 }
 ll Lucas(ll n, ll m, ll p)
 {
     if(m == )return ;
     return C(n % p, m % p, p) * Lucas(n / p, m / p, p) % p;
 }
 int main()
 {
     ll n, m, p;
     while(cin >> n >> m >> p)
     {
         if(n - m +  < m)
             cout<<""<<endl;
         else cout<<Lucas(n - m + , m, p)<<endl;
     }
     return ;
 }

D在F介绍完之后再介绍

E：hdu-4349

求C_(n,0),C _(n,1),C _(n,2)...C _(n,n)中奇数的数目

首先：组合数奇偶性判断公式：n  & m == m

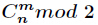
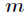
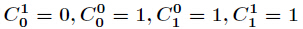
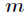
当然本题要判断的组合数很多，所以不能用上述结论，只能另辟蹊径。由于是判断奇偶性，那么就是判断  是否为1，利用Lucas定理，先把和化为二进制，这样它们都是01序列了。我们又知道    。这样中为0的地方对应的中的位置只有一种可能，那就是0。

这样我们可以不用管中为0的地方，只考虑中为1的位置，可以看出，中为1的位置对应的中为0或1，其结果都是1，这样答案就是：1<<(二进制表示中1的个数)

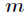
 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 const int maxn = 1e6 + ;
 const int mod = 1e9 + ;
 int lowbit(int x)
 {
     return x & (-x);
 }
 int main()
 {
     ll n, m, p;
     while(cin >> n)
     {
         int tot = ;
         while(n)
             n -= lowbit(n), tot++;
         cout<<(<<tot)<<endl;
     }
     return ;
 }

F：Gym - 100633J

扩展Lucas定理模板

这里的p不是素数，用中国剩余定理合并同余方程组。

详细介绍请看全文最开始的传送门

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 const int maxn = 1e6 + ;
 const int mod = 1e9 + ;
 ll pow(ll a, ll b, ll m)
 {
     ll ans = ;
     a %= m;
     while(b)
     {
         if(b & )ans = (ans % m) * (a % m) % m;
         b /= ;
         a = (a % m) * (a % m) % m;
     }
     ans %= m;
     return ans;
 }
 ll extgcd(ll a, ll b, ll& x, ll& y)
 //求解ax+by=gcd(a, b)
 //返回值为gcd(a, b)
 {
     ll d = a;
     if(b)
     {
         d = extgcd(b, a % b, y, x);
         y -= (a / b) * x;
     }
     else x = , y = ;
     return d;
 }
 ll mod_inverse(ll a, ll m)
 //求解a关于模上m的逆元
 //返回-1表示逆元不存在
 {
     ll x, y;
     ll d = extgcd(a, m, x, y);
     return d ==  ? (m + x % m) % m : -;
 }

 ll Mul(ll n, ll pi, ll pk)//计算n! mod pk的部分值  pk为pi的ki次方
 //算出的答案不包括pi的幂的那一部分
 {
     if(!n)return ;
     ll ans = ;
     if(n / pk)
     {
         for(ll i = ; i <= pk; i++) //求出循环节乘积
             if(i % pi)ans = ans * i % pk;
         ans = pow(ans, n / pk, pk); //循环节次数为n / pk
     }
     for(ll i = ; i <= n % pk; i++)
         if(i % pi)ans = ans * i % pk;
     return ans * Mul(n / pi, pi, pk) % pk;//递归求解
 }

 ll C(ll n, ll m, ll p, ll pi, ll pk)//计算组合数C(n, m) mod pk的值 pk为pi的ki次方
 {
     if(m > n)return ;
     ll a = Mul(n, pi, pk), b = Mul(m, pi, pk), c = Mul(n - m, pi, pk);
     ll k = , ans;//k为pi的幂值
     for(ll i = n; i; i /= pi)k += i / pi;
     for(ll i = m; i; i /= pi)k -= i / pi;
     for(ll i = n - m; i; i /= pi)k -= i / pi;
     ans = a * mod_inverse(b, pk) % pk * mod_inverse(c, pk) % pk * pow(pi, k, pk) % pk;//ans就是n! mod pk的值
     ans = ans * (p / pk) % p * mod_inverse(p / pk, pk) % p;//此时用剩余定理合并解
     return ans;
 }

 ll Lucas(ll n, ll m, ll p)
 {
     ll x = p;
     ll ans = ;
     for(ll i = ; i <= p; i++)
     {
         if(x % i == )
         {
             ll pk = ;
             while(x % i == )pk *= i, x /= i;
             ans = (ans + C(n, m, p, i, pk)) % p;
         }
     }
     return ans;
 }

 int main()
 {
     ll n, m, p;
     while(cin >> n >> m >> p)
     {
         cout<<Lucas(n, m, p)<<endl;
     }
     return ;
 }

D：HDU-4373

个for循环嵌套，有两种形式，第一类从1开始到，第二类从上一层循环当前数开始到，第一层一定是第一种类型，求总的循环的次数对364875103取余的结果。

首先可以看出，每一个第一类循环都是一个新的开始，与前面的状态无关，所以可以把个嵌套分为几个不

同的部分，每一个部分由第一类循环开始，最终结果相乘即可。剩下的就是第二类循环的问题，假设一个

层循环，最大到，分析一下得到如下结果

（1）只有一层，则循环次数为

（2）只有前两层，则循环次数为

（3）只有前三层，则循环次数为

由此得到结论：第的循环次数为

由于364875103=97 * 3761599

用中国剩余定理合并，但是不能直接套上述模板，会超时，上述模板是对于不同的合数p分解成质数的次方，算起来很麻烦，此处364875103就等于两个质数的乘积

这里a1 = 97, a2 = 3761599所以M1 = 3761599， M2 = 97， 求出M1关于m1的逆元，M2关于m2的逆元

然后之需要求出组合数mod97的值为a1，组合数mod3761599的值为a2

ans按照上述公式就可以直接算出来了。

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 const int maxn = 1e6 + ;
 ll pow(ll a, ll b, ll m)
 {
     ll ans = ;
     a %= m;
     while(b)
     {
         if(b & )ans = (ans % m) * (a % m) % m;
         b /= ;
         a = (a % m) * (a % m) % m;
     }
     ans %= m;
     return ans;
 }
 const ll mod1 = ;
 const ll mod2 = ;
 const ll mod = mod1 * mod2;
 ll fac1[mod1 + ], fac2[mod2 + ];
 ll inv1, inv2;
 void init()
 {
     fac1[] = fac2[] = ;
     for(int i = ; i < mod1; i++)fac1[i] = fac1[i - ] * i % mod1;
     for(int i = ; i < mod2; i++)fac2[i] = fac2[i - ] * i % mod2;
     inv1 = pow(mod2, mod1 - , mod1);//mod1 模上mod2的逆元
     inv2 = pow(mod1, mod2 - , mod2);//mod2 模上mod1的逆元 求出在之后的中国剩余定理合并的时候不用计算
 }

 ll C(ll n, ll m, ll p, ll fac[])
 {
     if(m > n)return ;
     return fac[n] * pow(fac[m] * fac[n - m], p - , p) % p;
 }

 ll Lucas(ll n, ll m, ll p, ll fac[])
 {
     if(m == )return ;
     return C(n % p, m % p, p, fac) * Lucas(n / p, m / p, p, fac) % p;
 }
 int main()
 {
     ll n, m, k, cases = ;
     ll a[];
     int T;
     init();
     cin >> T;
     while(T--)
     {
         cin >> n >> m;
         cin >> k;
         for(int i = ; i < k; i++)cin >> a[i];
         a[k] = m;
         ll ans = ;
         for(int i = ; i <= k; i++)
         {
             ll t = a[i] - a[i - ];
             ll a1 = Lucas(n + t - , t, mod1, fac1);
             ll a2 = Lucas(n + t - , t, mod2, fac2);
             ll a3 = (a1 * mod2 % mod * inv1 + a2 * mod1 % mod * inv2) % mod;//中国剩余定理合并同余方程组
             ans = ans * a3 % mod;
         }
         cout<<"Case #"<<++cases<<": "<<ans<<endl;
     }
     return ;
 }